
21.导数概 重点:导数和微分的 算 复合函数 能够热练计算初等函 隐函数和参数 法则 值,洛必达法则 极28 讲授 别函数性 调性 优化问 值概念讨 难点:导数的概 复合通数:式数 公式皮用 定理的发展历 辩证唯物主义思想 分的概念和性质 重点:不定积分和定 能热练计算函数的 分 其导 法和分部积分法 建立数学模型, 28 讲授 3,4 函数 转体的体积 定积分的微 难点:换元积分法和 体面图形的面积 分部积分法,微元法 近似与精确”“部分与整体“关系 四、课程考核评价方式 (一)考核方式 考核方式为闭卷笔试 考试课程成绩由平时成绩、期中成绩、期末成绩构成。 (二)课程成绩 平时成绩由学生课堂表现、作业、期中测验组成。平时成绩占课程考核成绩40%。 期末卷面成绩占课程考核成绩60%
10 二、一元函数微分学 第二章 导数与微分 2.1.导数概念 2.2.函数的求导法则 2.3.高阶导数 2.4.隐函数的导数 2.5.微分 第三章 中值定理与导数的运用 3.1.微分中值定理 3.2.洛必塔法则 3.3.泰勒公式 3.4.函数的单调性与曲线的凹凸性 3.5.函数的极值与最大最小值 3.6.函数图形的描绘 3.7. 曲率 思政融入点: 导数概念产生的背景及应用,中值 定理的发展历史, “变与不变”的 辩证唯物主义思想 能够熟练计算初等函 数的导数,利用极限, 连续,导数等相关数 学知识建立简单的数 学模型;能应用导数 正 确地 作出 函数 图 象,识别函数性态; 用函数极值概念讨论 优化问题; 重点:导数和微分的 概念,导数的四则运 算,复合函数、基本 初等函数、反函数、 隐函数和参数方程求 导,罗尔中值定理, 拉格朗日中值定理, 函数的的单调性,极 值,洛必达法则。 难点:导数的概念, 复合函数、隐函数及 参 数方 程式 函数 求 导,三个中值定理, 泰勒公式及其应用 28 讲授 2 三)一元函数积分学 第四章 不定积分 4.1.不定积分的概念和性质 4.2.换元积分法 4.3.分部积分法 第五章 定积分 5.1.定积分的概念 5.2.定积分的性质 5.3.微积分基本公式 5.4.定积分的换元法和分部积分法 5.5.广义函数积分 第六章 定积分的应用 6.1.定积分的微元法 6.2.平面图形的面积 6.3.体积 思政融入点:微积分基本公式的发 展历史,定积分概念的产生和应用, “近似与精确”“部分与整体”关系. 能够熟练计算函数的 不定积分,定积分, 反常积分。熟练应用 微 元法 分析 实际 问 题,建立数学模型, 解决实际问题。 重点:不定积分和定 积分的概念性质,换 元积分法和分部积分 法,积分上限函数及 其导数,N-L 公式, 平面图形的面积和旋 转体的体积 难点:换元积分法和 分部积分法,微元法 28 讲授 3,4 四、课程考核评价方式 (一)考核方式 考核方式为闭卷笔试。 考试课程成绩由平时成绩、期中成绩、期末成绩构成。 (二)课程成绩 平时成绩由学生课堂表现、作业、期中测验组成。平时成绩占课程考核成绩 40%。 期末卷面成绩占课程考核成绩 60%
1.考核环节及说明 成绩构成 考核说明 (1)平时成绩满分为100分,占总成绩的40% 平时成结 (2)其中课堂表现占总成绩10%,积极参与课堂教学活动,认真完成小组任务,无扰乱课 堂秩序的行为,不迟到不缺课,计10分。作业占20%。认真,按时完成作业,不抄袭,不 缺漏。计20分。期中测验占10%,成绩的评定根据试卷参考答案和评分标准进行。 (1)考试方式及占比:采用闭卷笔试,考试成绩100分,占课程考核成绩的60%。 (2)评定依据:考试成绩的评定根据试卷参考答案和评分标准进行, 期末考试 (3)考试题型:包含单项选择题、填空题、计算题等。 (4)考试内容:主要考核函数,极限、导数与微分、微分中值定理与导数的应用、不定积 分、定积分、定积分的应用等知识点的掌握程度。 2.考核与评价方式 成绩比例(平时成绩40%期末成绩60%) 课程目标 平时成绩(40%) 期末成绩 合计 作业 课堂表现 期中测验 (60%) (20%) (10%) (10%) 1 6 3 13 27 2 7 3 5 21 36 3 4 0 37 4 / 合计(成绩构成) 20 10 10 60 100 五、教学方法 本课程在教学上主要采用教师讲解、演算、提问,讨论等方式教授。紧扣“课堂讲授 课程讨论、作业训练、考核”等教学要素灵活采用多种形式教学,同时辅以微课视频供学生 在线学习。习题辅导答疑采用现场答疑+QQ+微信+网络教学平台多种方式。 六、参考材料 线上:智慧树:https://www2 hihuishu.coml 线下: 1.《高等数学》(上、下册),同济大学应用数学系编,高等教有出版社,2018年8月,第7 版 2.《高等数学》(上、下册),上海交通大学数学系编,上海交通大学出版社,2015年8月 第2版
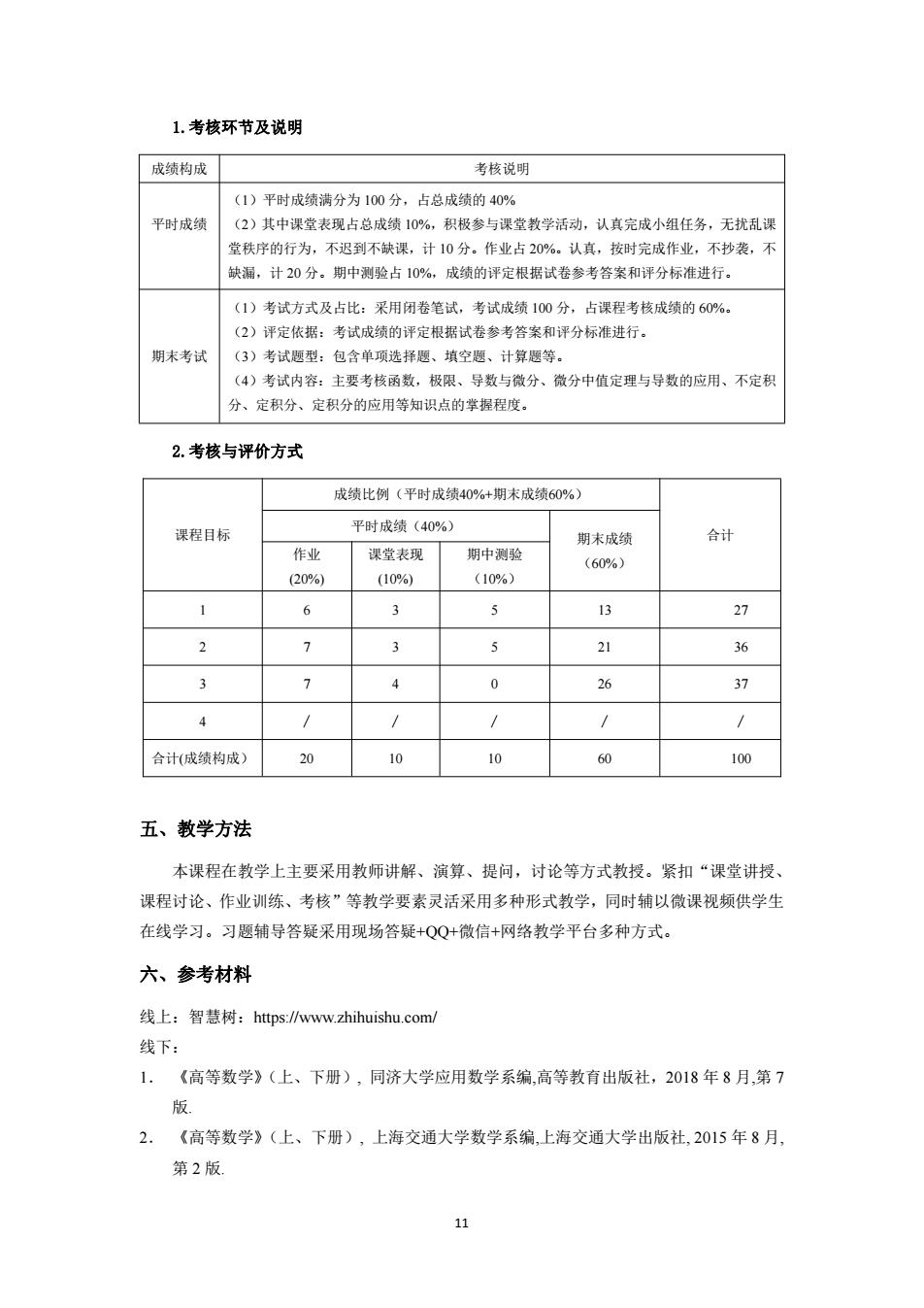
11 1.考核环节及说明 成绩构成 考核说明 平时成绩 (1)平时成绩满分为 100 分,占总成绩的 40% (2)其中课堂表现占总成绩 10%,积极参与课堂教学活动,认真完成小组任务,无扰乱课 堂秩序的行为,不迟到不缺课,计 10 分。作业占 20%。认真,按时完成作业,不抄袭,不 缺漏,计 20 分。期中测验占 10%,成绩的评定根据试卷参考答案和评分标准进行。 期末考试 (1)考试方式及占比:采用闭卷笔试,考试成绩 100 分,占课程考核成绩的 60%。 (2)评定依据:考试成绩的评定根据试卷参考答案和评分标准进行。 (3)考试题型:包含单项选择题、填空题、计算题等。 (4)考试内容:主要考核函数,极限、导数与微分、微分中值定理与导数的应用、不定积 分、定积分、定积分的应用等知识点的掌握程度。 2.考核与评价方式 课程目标 成绩比例(平时成绩40%+期末成绩60%) 合计 平时成绩(40%) 期末成绩 (60%) 作业 (20%) 课堂表现 (10%) 期中测验 (10%) 1 6 3 5 13 27 2 7 3 5 21 36 3 7 4 0 26 37 4 ∕ ∕ ∕ ∕ ∕ 合计(成绩构成) 20 10 10 60 100 五、教学方法 本课程在教学上主要采用教师讲解、演算、提问,讨论等方式教授。紧扣“课堂讲授、 课程讨论、作业训练、考核”等教学要素灵活采用多种形式教学,同时辅以微课视频供学生 在线学习。习题辅导答疑采用现场答疑+QQ+微信+网络教学平台多种方式。 六、参考材料 线上:智慧树:https://www.zhihuishu.com/ 线下: 1. 《高等数学》(上、下册), 同济大学应用数学系编,高等教育出版社,2018 年 8 月,第 7 版. 2. 《高等数学》(上、下册), 上海交通大学数学系编,上海交通大学出版社, 2015 年 8 月, 第 2 版

3。《托马斯微积分》,叶其孝、王耀东等译,高等教有出版社,2016年6月,第10版 4.《微积分》(上、下册),主编:James Stewar,高等教有出版社,2014年6月,第8版 5.《微积分》(上、下册),同济大学应用数学系编,高等教有出版社,1999年9月,第3 版 6.《工科数学分析基础》(上、下册),主编:马知思王绵森,高等教育出版社,2017年8 月,第3版 7.《数学分析》(上、下册),华东师大数学系编,高等教育出版社,2019年5月,第5 版 8.《高等数学释疑解难》,工科数学课程教学指导委员会编高等教有出版社,2016年6 月第2版 9.《高等数学附册学习辅导与习题选解》,同济大学应用数学系编,同济大学出版社,2014 年8月,第7版 10.《高等数学教与学参考》,主编:张宏志,西北工业大学出版社,2017年9月,第1版 主撰人:朱红鲜 审核人:刘太岗、王晓明 英文校对:王晓明 教学副院长:袁红春 日期:2022年9月3日
12 3. 《托马斯微积分》, 叶其孝、王耀东等译, 高等教育出版社, 2016 年 6 月,第 10 版. 4. 《微积分》(上、下册), 主编: James Stewart, 高等教育出版社, 2014 年 6 月,第 8 版. 5. 《微积分》(上、下册), 同济大学应用数学系编, 高等教育出版社, 1999 年 9 月,第 3 版. 6. 《工科数学分析基础》(上、下册), 主编:马知恩 王绵森, 高等教育出版社, 2017 年 8 月,第 3 版. 7. 《数学分析》(上、下册), 华东师大数学系编, 高等教育出版社, 2019 年 5 月,第 5 版. 8. 《高等数学释疑解难》, 工科数学课程教学指导委员会编 高等教育出版社, 2016 年 6 月,第 2 版. 9. 《高等数学附册学习辅导与习题选解》, 同济大学应用数学系编,同济大学出版社, 2014 年 8 月,第 7 版. 10. 《高等数学教与学参考》, 主编:张宏志, 西北工业大学出版社, 2017 年 9 月,第 1 版. 主撰人:朱红鲜 审核人:刘太岗、王晓明 英文校对:王晓明 教学副院长:袁红春 日 期:2022 年 9 月 3 日
附件:各类考核与评价标准表 1.作业和课堂表现成绩评分标准 成绩 优秀 良好 中等 及格 不及格 课程目标 (分数290分) 78≤分数<90 (68≤分数<78) (60≤分数<68) (分数<60分) 课能认真听 上课基本能认直听 不能上课认真 课程目标 (33%) 有作 正硬 规 正 缺不 不峡不法 部分 有缺 ,能较正确回 能基本正 课程目标2 析所有作业,远 正确分析所有 正确分析 分析 成高 (30%) 不不漏: 书写较规范, 写基本规,部 书不规范, 线正确标用知 用 本正确运用知 课程目标3 业所有澳 作业 分析部分 (37%) 晰,书写规范,不 书规范不清,书写不规范 书写 缺不漏 衣较正确。 述不正确。 2,期中测验考核与评价标准 成绩 优秀 良好 中等 及格 不及格 课程标 (分数e90分) (78≤分数<90) (68≤分数<78) (60≤分数<68) (分数<60分) 米程日标1 的智各欢风能确解套收风重正角解套7网能正自解紧不能正答 逻锻拉洁城 (50% 确,逻辑较清晰。 确,逻辑基本清晰。表述不准确,逻轩 果程目标】 能正确解答90风能正确解90 能正确解容90%以上 的解容90网 (50%) 确,逻辑清。 确,逻辑较清晰。 ,逻辑较清晰。 确,逻辑基本清晰。 不准响,辑不 3.期末考核与评价标准 、成绩 优秀 良好 中等 及格 不及格 课程目标 (分心90分 (78≤分数<90) (68≤分数<78 (60≤分数<68 (分数<60分) 能正确解答 (22%) 准确,逻辑洁晰 确,逻细 确,逻辑 本准 逻辑基本 准确,逻辑不清晰】 裸程目标2 表上的. (35%) 纹准油 逻辑 角解答 课程目标3以上的园自深 以上的题目 的题目 (43%) 准确,逻辑清晰 准确,逻辑 较确,逻辑 让确,逻辑基本 准确,逻辑不清晰
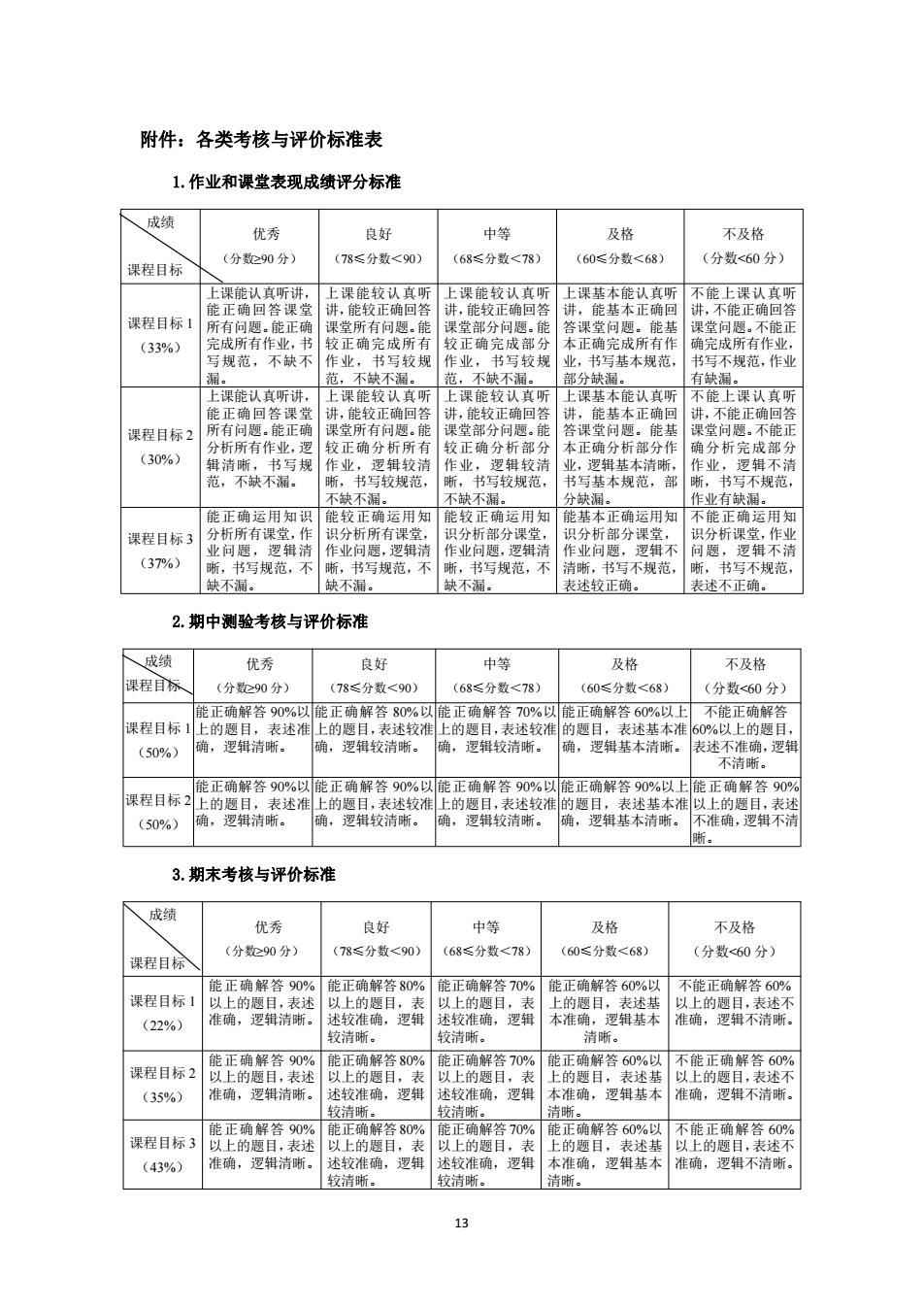
13 附件:各类考核与评价标准表 1.作业和课堂表现成绩评分标准 成绩 课程目标 优秀 (分数≥90 分) 良好 (78≤分数<90) 中等 (68≤分数<78) 及格 (60≤分数<68) 不及格 (分数<60 分) 课程目标 1 (33%) 上课能认真听讲, 能正确回答课堂 所有问题。能正确 完成所有作业,书 写规范,不缺不 漏。 上课能较认真听 讲,能较正确回答 课堂所有问题。能 较正确完成所有 作业,书写较规 范,不缺不漏。 上课能较认真听 讲,能较正确回答 课堂部分问题。能 较正确完成部分 作业,书写较规 范,不缺不漏。 上课基本能认真听 讲,能基本正确回 答课堂问题。能基 本正确完成所有作 业,书写基本规范, 部分缺漏。 不能上课认真听 讲,不能正确回答 课堂问题。不能正 确完成所有作业, 书写不规范,作业 有缺漏。 课程目标 2 (30%) 上课能认真听讲, 能正确回答课堂 所有问题。能正确 分析所有作业,逻 辑清晰,书写规 范,不缺不漏。 上课能较认真听 讲,能较正确回答 课堂所有问题。能 较正确分析所有 作业,逻辑较清 晰,书写较规范, 不缺不漏。 上课能较认真听 讲,能较正确回答 课堂部分问题。能 较正确分析部分 作业,逻辑较清 晰,书写较规范, 不缺不漏。 上课基本能认真听 讲,能基本正确回 答课堂问题。能基 本正确分析部分作 业,逻辑基本清晰, 书写基本规范,部 分缺漏。 不能上课认真听 讲,不能正确回答 课堂问题。不能正 确分析完成部分 作业,逻辑不清 晰,书写不规范, 作业有缺漏。 课程目标 3 (37%) 能正确运用知识 分析所有课堂,作 业问题,逻辑清 晰,书写规范,不 缺不漏。 能较正确运用知 识分析所有课堂, 作业问题,逻辑清 晰,书写规范,不 缺不漏。 能较正确运用知 识分析部分课堂, 作业问题,逻辑清 晰,书写规范,不 缺不漏。 能基本正确运用知 识分析部分课堂, 作业问题,逻辑不 清晰,书写不规范, 表述较正确。 不能正确运用知 识分析课堂,作业 问题,逻辑不清 晰,书写不规范, 表述不正确。 2.期中测验考核与评价标准 成绩 课程目标 优秀 (分数≥90 分) 良好 (78≤分数<90) 中等 (68≤分数<78) 及格 (60≤分数<68) 不及格 (分数<60 分) 课程目标 1 (50%) 能正确解答 90%以 上的题目,表述准 确,逻辑清晰。 能正确解答 80%以 上的题目,表述较准 确,逻辑较清晰。 能正确解答 70%以 上的题目,表述较准 确,逻辑较清晰。 能正确解答 60%以上 的题目,表述基本准 确,逻辑基本清晰。 不能正确解答 60%以上的题目, 表述不准确,逻辑 不清晰。 课程目标 2 (50%) 能正确解答 90%以 上的题目,表述准 确,逻辑清晰。 能正确解答 90%以 上的题目,表述较准 确,逻辑较清晰。 能正确解答 90%以 上的题目,表述较准 确,逻辑较清晰。 能正确解答 90%以上 的题目,表述基本准 确,逻辑基本清晰。 能正确解答 90% 以上的题目,表述 不准确,逻辑不清 晰。 3.期末考核与评价标准 成绩 课程目标 优秀 (分数≥90 分) 良好 (78≤分数<90) 中等 (68≤分数<78) 及格 (60≤分数<68) 不及格 (分数<60 分) 课程目标 1 (22%) 能正确解答 90% 以上的题目,表述 准确,逻辑清晰。 能正确解答80% 以上的题目,表 述较准确,逻辑 较清晰。 能正确解答 70% 以上的题目,表 述较准确,逻辑 较清晰。 能正确解答 60%以 上的题目,表述基 本准确,逻辑基本 清晰。 不能正确解答 60% 以上的题目,表述不 准确,逻辑不清晰。 课程目标 2 (35%) 能正确解答 90% 以上的题目,表述 准确,逻辑清晰。 能正确解答80% 以上的题目,表 述较准确,逻辑 较清晰。 能正确解答 70% 以上的题目,表 述较准确,逻辑 较清晰。 能正确解答 60%以 上的题目,表述基 本准确,逻辑基本 清晰。 不能正确解答 60% 以上的题目,表述不 准确,逻辑不清晰。 课程目标 3 (43%) 能正确解答 90% 以上的题目,表述 准确,逻辑清晰。 能正确解答80% 以上的题目,表 述较准确,逻辑 较清晰。 能正确解答 70% 以上的题目,表 述较准确,逻辑 较清晰。 能正确解答 60%以 上的题目,表述基 本准确,逻辑基本 清晰。 不能正确解答 60% 以上的题目,表述不 准确,逻辑不清晰
1.3课程1101456《高等数学C(1)》教学大纲 一、课程基本信息 中文名称:高等数学C(1) 课程名称 英文名称:Advanced Mathematics C() 课程号 101456 学分 学时 总学时:80 讲投学时 实验学时 上机学时 讨论学时 80 0 0 0 开误学院 信息学院 开课学 第1学期 课程负责人 王晓明 适用专业 经济管理类专 先修课程及要求 无 二、课程简介 (一)课程概况 本课程的研究对象是函数(变化过程中量的依赖关系)。内容包括函数、极限、连续, 一元函数微分学,一元函数积分学。要通过各个教学环节逐步培养学生的抽象思维能力、逻 辑推理能力、空间想象能力和自学能力,还要特别注意培养学生的熟练运算能力和综合运用 所学知识去分析解决问题的能力。 The fundamental objects that we deal with in advanced mathematics are functions.It has two main parts:differential calculus and integral calculus Through this couse,students are gradually trained to have the ability to abstract and generalize problems,initial logical reasoning ability. self-learning ability and certain computing ability.It lays the foundation for students to learn the succeeding courses and to gain further knowledge of science and technology in the future (二)课程目标 课程目标1:能建立变量数学的思想,为整个微积分确立研究对象,能对经济及工程问 题中变量数学问愿进行正确数学表达,能够运用严格数学语言论证极限问题:能从中国古代 的极限思想建立民族自豪感和责任感,民族凝聚力。 课程目标2:能从客观事物的某种数量关系或空间形式中抽象出数学模型:能利用变量 对实际工程问题进行建模:能借助概念产生的来源背景和实际生活中的例子对其抽象、概括、 归纳求解:能够运用极限思想分析问题,并利用所学函数连续、可导相关数学知识建立简单 的数学模型:能用函数的导数求边际函数和弹性函数,并能解释其经济意义。 课程目标3:能应用导数正确地作出函数图象:能够利用泰勒展式来识别判断实际经济 和工程问题,用函数极值概念讨论优化问题:能用函数的导数求解经济函数的最优化问题: 通过数学发展的三次危机的解决,认同危机与机遇并存,只要坚定科学的理念、正确的学习 14
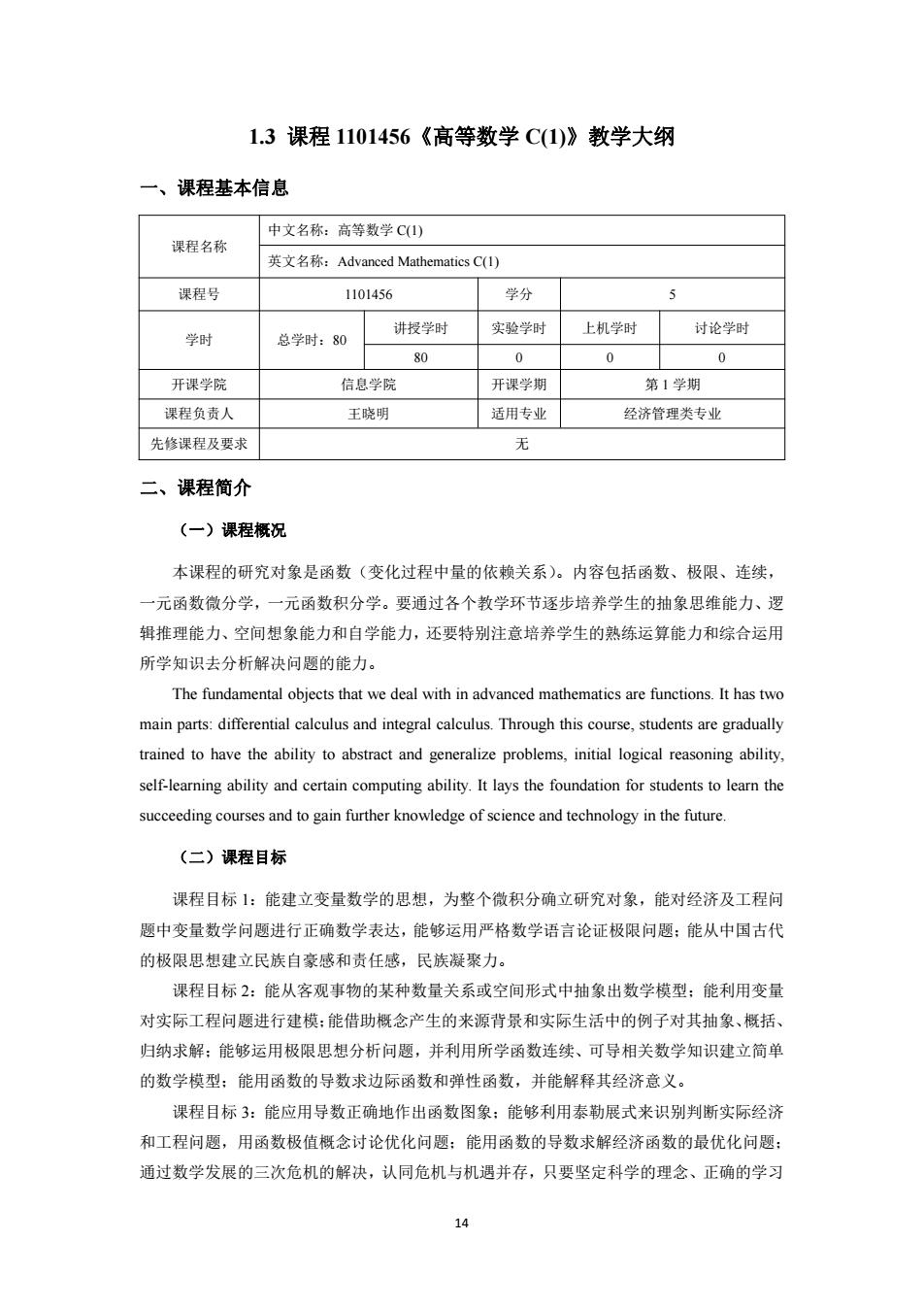
14 1.3 课程 1101456《高等数学 C(1)》教学大纲 一、课程基本信息 课程名称 中文名称:高等数学 C(1) 英文名称:Advanced Mathematics C(1) 课程号 1101456 学分 5 学时 总学时:80 讲授学时 实验学时 上机学时 讨论学时 80 0 0 0 开课学院 信息学院 开课学期 第 1 学期 课程负责人 王晓明 适用专业 经济管理类专业 先修课程及要求 无 二、课程简介 (一)课程概况 本课程的研究对象是函数(变化过程中量的依赖关系)。内容包括函数、极限、连续, 一元函数微分学,一元函数积分学。要通过各个教学环节逐步培养学生的抽象思维能力、逻 辑推理能力、空间想象能力和自学能力,还要特别注意培养学生的熟练运算能力和综合运用 所学知识去分析解决问题的能力。 The fundamental objects that we deal with in advanced mathematics are functions. It has two main parts: differential calculus and integral calculus. Through this course, students are gradually trained to have the ability to abstract and generalize problems, initial logical reasoning ability, self-learning ability and certain computing ability. It lays the foundation for students to learn the succeeding courses and to gain further knowledge of science and technology in the future. (二)课程目标 课程目标 1:能建立变量数学的思想,为整个微积分确立研究对象,能对经济及工程问 题中变量数学问题进行正确数学表达,能够运用严格数学语言论证极限问题;能从中国古代 的极限思想建立民族自豪感和责任感,民族凝聚力。 课程目标 2:能从客观事物的某种数量关系或空间形式中抽象出数学模型;能利用变量 对实际工程问题进行建模;能借助概念产生的来源背景和实际生活中的例子对其抽象、概括、 归纳求解;能够运用极限思想分析问题,并利用所学函数连续、可导相关数学知识建立简单 的数学模型;能用函数的导数求边际函数和弹性函数,并能解释其经济意义。 课程目标 3:能应用导数正确地作出函数图象;能够利用泰勒展式来识别判断实际经济 和工程问题,用函数极值概念讨论优化问题;能用函数的导数求解经济函数的最优化问题; 通过数学发展的三次危机的解决,认同危机与机遇并存,只要坚定科学的理念、正确的学习