
3 汇交力系 M,=M,(匠) Fe=∑月 4,=M,) 力偶系 M=∑M(匠) M=M,()
F1 F2 F3 o 汇交力系 力偶系 M1 Mo F1 M3 Mo F3 M2 Mo F2 FR Fi M Mo Fi = F1 o F2 F3 = o
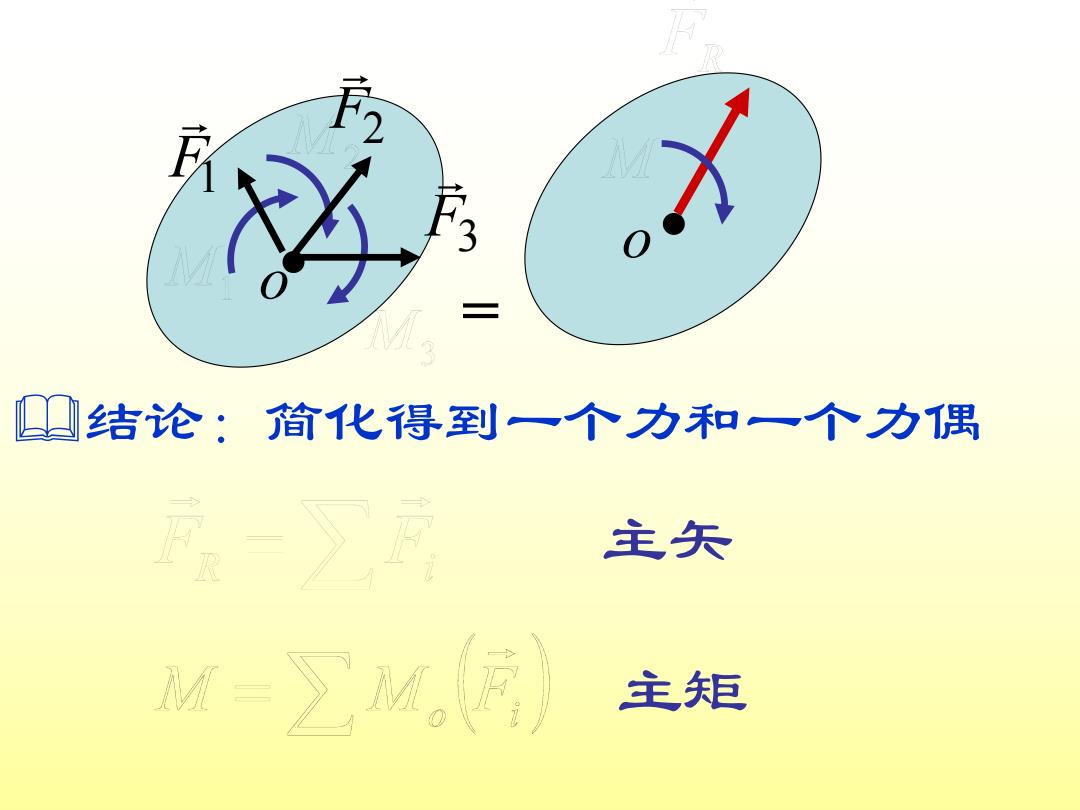
四结论:简化得到一个力和一个力偶 主矢 法-∑M 主矩
o = o F1 F2 F3 &结论:简化得到一个力和一个力偶 主矢 主矩
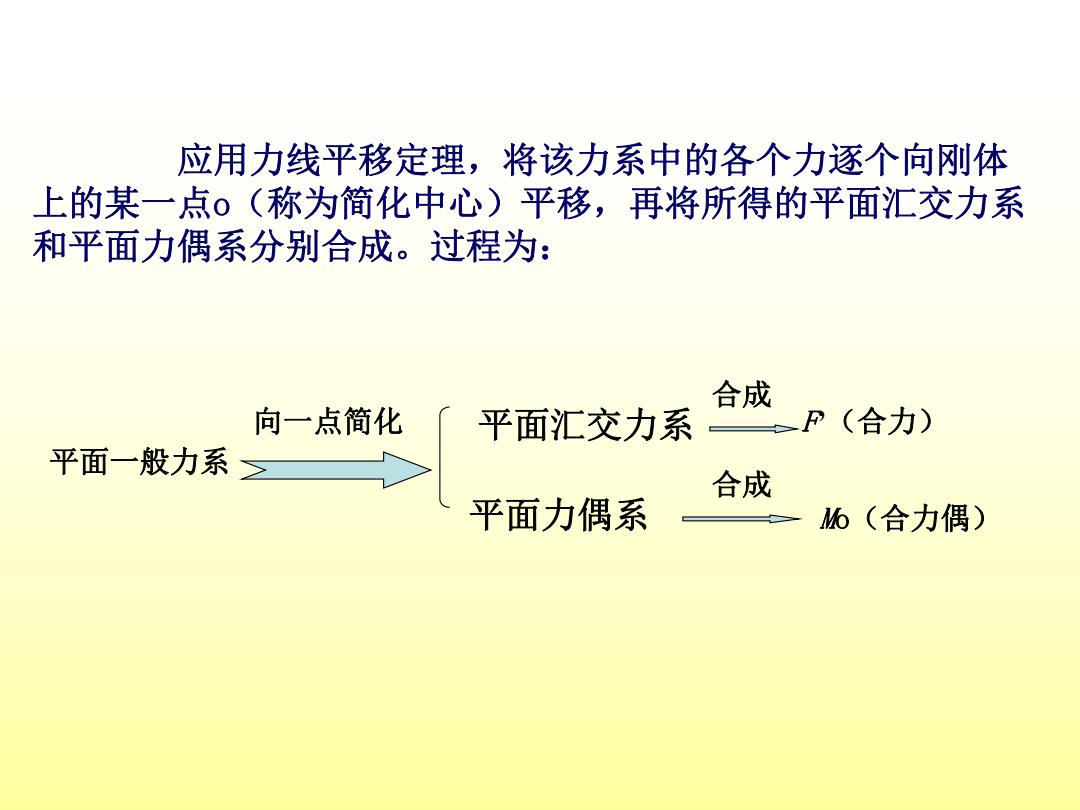
应用力线平移定理,将该力系中的各个力逐个向刚体 上的某一点0(称为简化中心)平移,再将所得的平面汇交力系 和平面力偶系分别合成。过程为: 合成 向一点简化 平面汇交力系 P(合力) 平面一般力系 合成 平面力偶系 6(合力偶)
平面一般力系 平面力偶系 向一点简化 平面汇交力系 合成 合成 F’(合力) Mo(合力偶) 应用力线平移定理,将该力系中的各个力逐个向刚体 上的某一点o(称为简化中心)平移,再将所得的平面汇交力系 和平面力偶系分别合成。过程为:
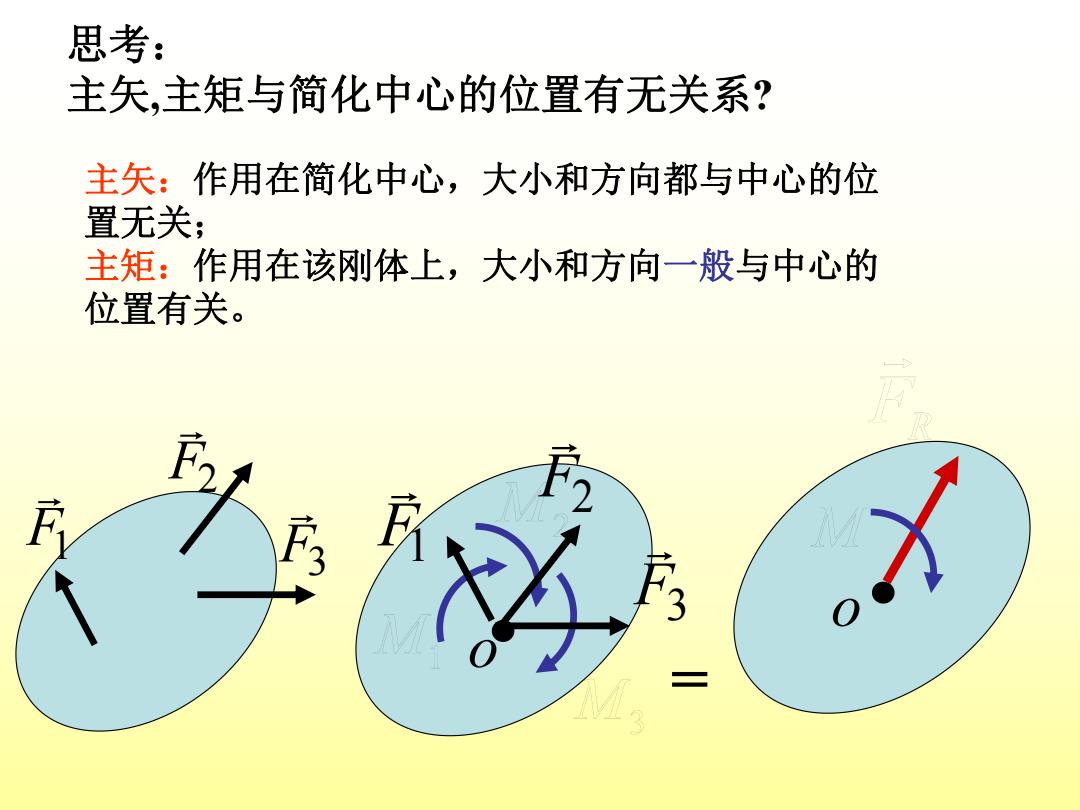
思考: 主矢,主矩与简化中心的位置有无关系? 主矢:作用在简化中心,大小和方向都与中心的位 置无关; 主矩:作用在该刚体上,大小和方向一般与中心的 位置有关
主矢:作用在简化中心,大小和方向都与中心的位 置无关; 主矩:作用在该刚体上,大小和方向一般与中心的 位置有关。 F1 F2 F3 思考: 主矢,主矩与简化中心的位置有无关系? o = o F1 F2 F3

FR'=F'+F'2+…+Fn'=+F+…+Fn=∑F 事实上,可直接用原力系(F,F2,…,Fm)中的各力 作出力多边形,力多边形的封闭边称为原力系的主矢。F 的大小和方向等于主矢,作用点在0点。 由此可见,主矢与简化中心的位置有关。 M=M+M2++M,=M()+M(E)++M(E)=∑M(F 由此可见,Mo一般与简化中心的位置有关,它反映 了原力系中各力的作用线相对于O点的分布情况,称为 原力系对O点的主矩
由此可见,主矢与简化中心的位置有关。 FR ' F ' 1 F ' 2 F n ' F1 F2 F n F 事实上,可直接用原力系(F1,F2,···,Fn)中的各力 作出力多边形,力多边形的封闭边称为原力系的主矢。FR ‘ 的大小和方向等于主矢,作用点在O点。 由此可见,Mo一般与简化中心的位置有关,它反映 了原力系中各力的作用线相对于O点的分布情况,称为 原力系对O点的主矩。 M ( ) ( ) ( ) ( ) 0 M1M2 Mn Mo F1 Mo F2 Mo Fn Mo F