
因此,其解具有与方程(1.5)相同的形式,我们得到: d=ocospt+sinpt (1.8) 式中中,和中,分别为在初始时刻t=0该盘的角位移和角速度。如前节那样,我们从方程(1.8) 得出结论:旋转振动的周期为: ==2 (1.9) p 其频率为: (1.10) 在长度为1、直径为d的圆形横截面轴的情说下,其扭转弹赞常数可以用下列公式◆来 表达: GJπdG k,二I =321 (c) 式中G为材料的剪切弹性模量。方程(◇)中符号J代表轴的横截面的扭转常数,当横截面 为圆形时,它等于极惯性矩。通常扭转弹簧常数,以磅-英寸/弧度为单位。 另外,如果圆盘是均匀的,直径为D,重量为W,那么其质量惯性矩则为: 1、形D 8g (d) 采用这些,值和I值,扭转振动的周期和频率可以从方程(1.9)和(1.10)求得。 在非圆形横截面轴或不规则形状物体这种较为一般的情况下,k和I两个量计算起来可 能较为困难。然而,如果它们的求算没有公式可以利用的话,用实验一般是可以确定的。为 了使振动为纯旋转振动,必须将轴的轴线与通过物体质量中心的主轴相吻合。否则,则需要 引进约束(成轴承方式)阻止物体的其它运动。还应注意旋转振动可能在不涉及扭转变形的 系统中发生(见本节末尾处的例题2)。 前面整个讨论中,假设图1,8中轴为直径d的均匀横藏面,如果该轴由长度分别为1:和 12以及直径为d,和dz的两部分组成,那么各扭转弹簧常数k,1和k,2可以从方程(c)求算出 来。于是,轴的两部分代表串联着的扭转弹簧,其等效弹簧常数可以从前节中的方程()来 得到。 ·阶梯形轴的情况也可以另一方式来处理。如果由两部分组成的轴承受扭矩M,那么该轴 的总扭角将为: 6=名+总=是器+2器-%,+器) k,1 可以看到,具有两个直径d:和d2的轴的扭角,与等直径为d,并用下列方程给予修正长度为 L,的轴的扭角相同。 N L1=l1+la月 di (e) 长度为L1、直径为d1的轴与所给两个不同直径的轴,具有相同的弹簧常数,该轴是为此情 况下的等效轴。 ·见Timoshenko和Young着Elements of Strength of Materials,.第5版,第72页

E ·10* 现在让我们考虑一根轴,支承于无摩婆的轴承中,且每一端处带有一个旋转物体的情 况,如图1.9所示。这是实用中重要的情况, 因为它可以考虑代表一端带有一个推进器,另 一端带有一个轮机马达的推进器的轴*。如果 两个盘按相反方向扭转,然后突然放松,那么 将发生扭转振动。根据角动量的守恒原理得 曾 出:在这样一种振动过程中,这两个盘必定总 地 按相反方向转动。因而,位于轴上P点的某一 中间横截面(见图1.9)保持不动,该横裁面称 ·为结点截面。它的位置根据这两个物体具有相 图1.9 同的振动周期这一事实来求出,因为不是这祥 的话,那么它们总按相反方向转动的情况将不会得到实现。 将方程(1.9)用于结点截面两侧两个分系统的每一分系统上,我们得到: == k,2 (f) 式中,:和k,分别为轴的左边部分和右边部分的弹簧常数。从方程(c)看到,这些量与该 轴相应部分的长度成反比,所以从方程(手)得出: a 671 于是,由于a+b=1,我们求出: a=T+I: b=Ttl. (9) 将方程(1.9)和(1.10)用于该系统的左边部分,我们得到: r=2x/=2r√ 3211:12 ,1 d+G(I,+I2) (1.11) f=1VidG(+1) 2北 32111: (1.12) 从这些公式,只要轴的尺寸、模量G和诸端处物体的质量惯性矩均为已知,扭转振动的周期 和频率就可以求算出来。在我们现在的讨论中,轴的质量略去不计,它对振动周期的影响将 在后面第1,4节中讨论。 从方程(9)可以看到,如果转动的物体之一与另一个相比具有很大的质量惯性矩,那 么结点横截面可以取于较大的物体处,而且带有两个物体的系统,(图1.9),简化成仅带有一 个物体的系统(图1.8)。 例题1参见图1.9,假设在轴的两端两个均匀盘具有重量W1=1000磅和W。=2000磅, 直径D1=50英寸和D2=75英寸,而轴的长度1=120英寸,轴的直径d=4英寸,剪切模量 G=12×10磅英寸。试求算该系统的自由扭转振动的频本。如果沿64英寸长度,轴的直 径从4英寸增大为8英寸,试问,此频率按什么比例增大? 解:应用方程(d)中所给的数据,我们求算出诸盘的质量惯性矩为: 1=(1000)(50)2 (8)(386)=809磅-英寸-秒2 ·这是工程师们发现带要作扭转振动研光的最早问题之一
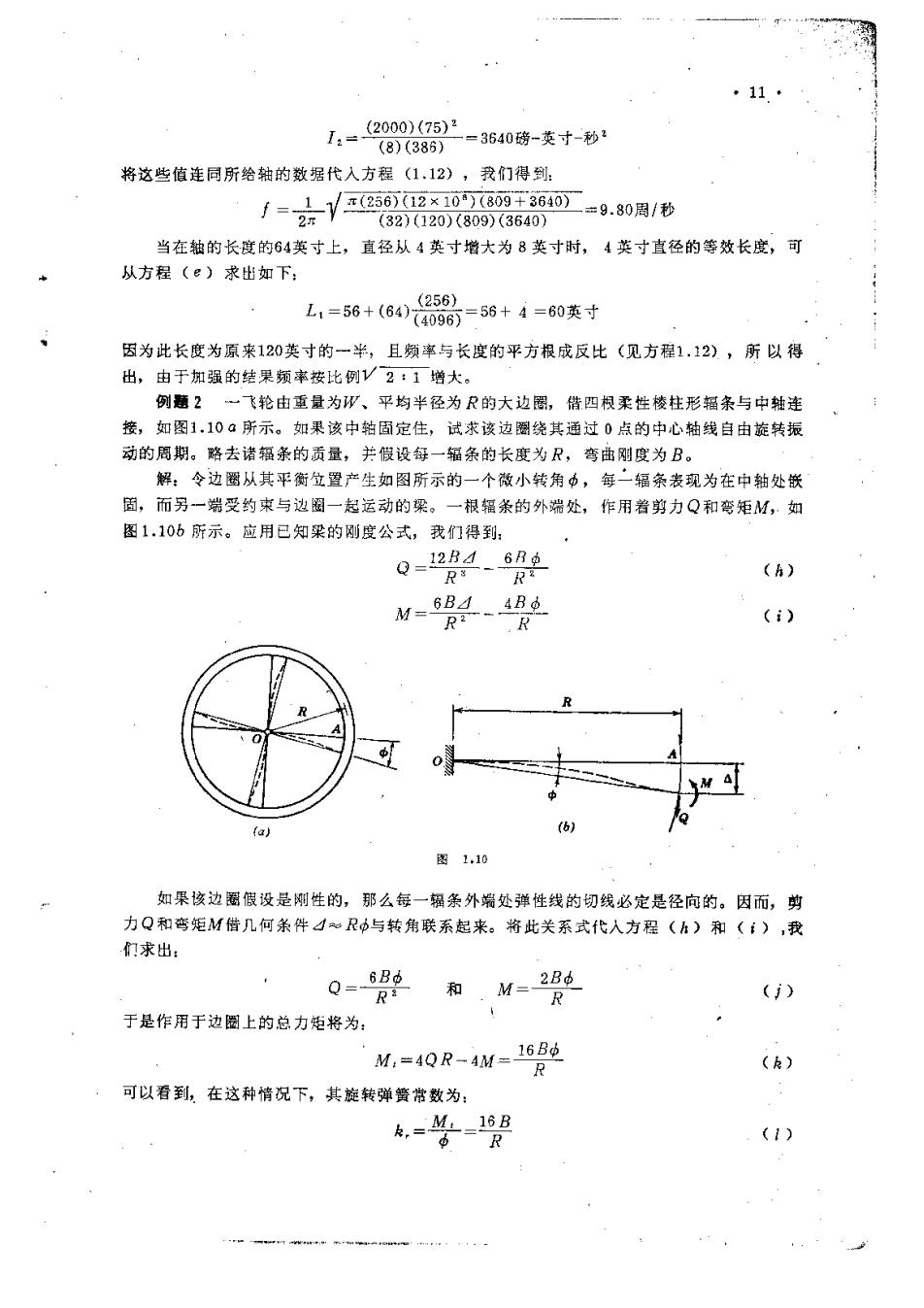
11 12=2000)(75)2 (8)(386) =3640磅-英寸-秒2 将这些值连同所给轴的数据代入方程(1.12),我们得到: /-2六V在202S08t60=9.30用/ (32)(120)(809)(3640) 当在轴的长度的64英寸上,直径从4英寸增大为8英寸时,4英寸直径的等效长度,可 从方程(e)求出如下: L1=56+(6496=56+4=0英寸 因为此长度为原来120英寸的一半,且频率与长度的平方根成反比(见方程1.12),所以得 出,由于加强的结果频率按比例V2:1增大。 例题2一飞轮由重量为W、平均半径为R的大边圈,偕四权柔性棱柱形辐条与中轴连 接,如图1.10a所示。如果该中轴固定住,试求该边圈绕其通过0点的中心轴线自由旋转振 动的周期。略去诸辐条的质量,并假设每一辐条的长度为R,弯曲刚度为B。 解:令边圈从其平衡位置产生如图所示的一个微小转角中,每一辐条表现为在中轴处嵌 固,而另一端受约束与边圈一起运动的梁。一根辐条的外端处,作用着剪力Q和弯矩M,·如 图1.10b所示。应用已知梁的刚度公式,我们得到: Q=12B4、6né R8■ R名 (存) M=6B☑4B6 R2、 R () R 0 (a) (6) 图110 如果该边圈假设是刚性的,那么每一辐条外端处弹性线的切线必定是径向的。因而,剪 力Q和弯矩M借几何条件心R中与转角联系起来。将此关系式代入方程()和(),我 们求出: Q=-6Bd R2 和.M=2B6 R (j) 于是作用于边圈上的总力矩将为: M,=4QR-4M=16B R (k) 可以看到,在这种情况下,其旋转弹簧常数为: ,=4=16B R (1)
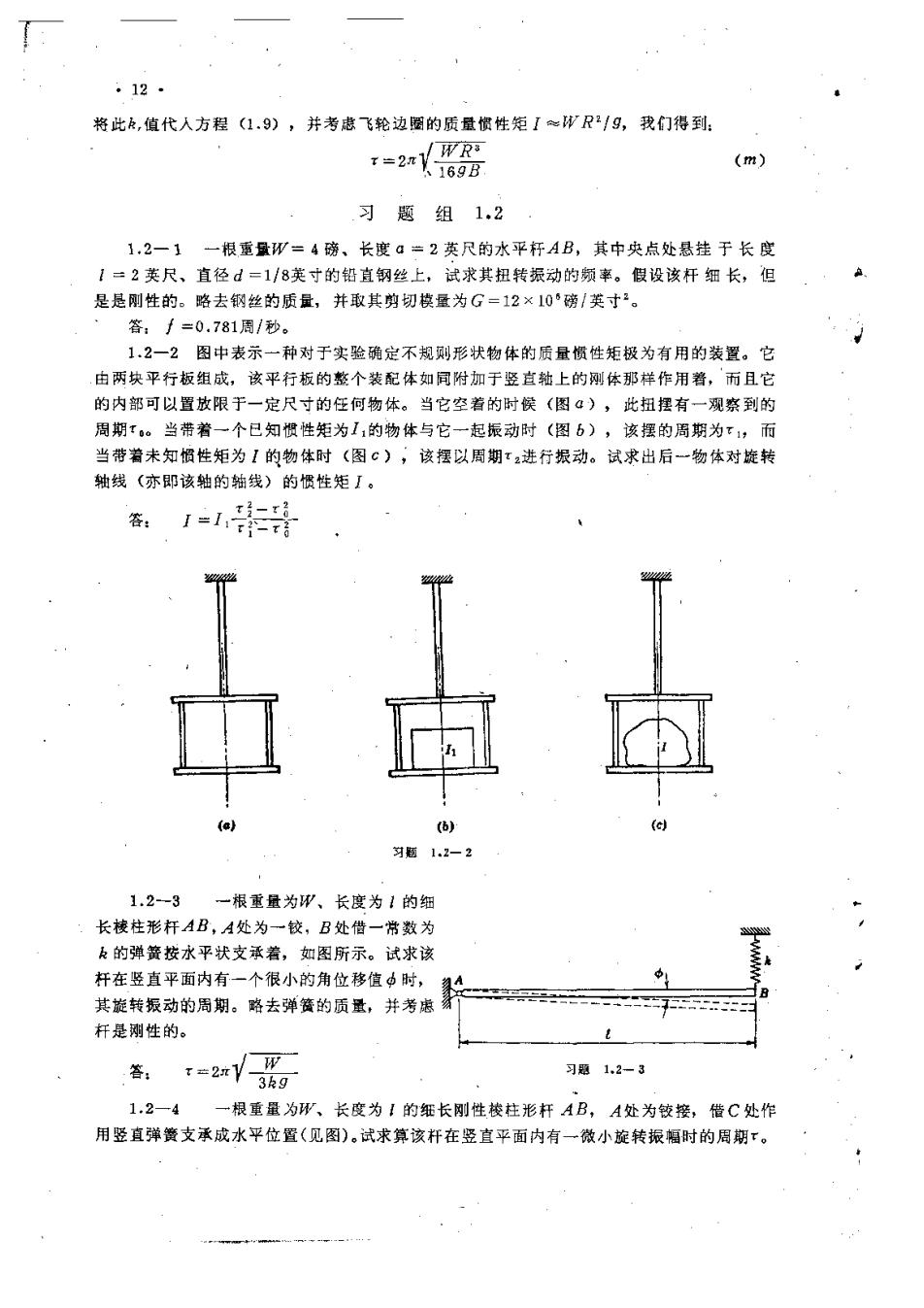
。12· 将此,值代人方程(1.9),并考虑飞轮边圈的质量惯性矩I≈成R2/9,我们得到: T=2nyWRi V169B (m) 习题组1.2 1,2一1一根重量刑=4磅、长度G兰2英尺的水平杆AB,其中央点处悬挂于长度 1=2英尺、直径d=1/8英寸的铅直钢丝上,试求其扭转振动的颜率。假设该杆细长,但 是是刚性的。略去钢丝的质量,并取其剪切模量为G=12×10‘磅/英寸2。 答:∫=0.781周/秒。 1.2一2图中表示一种对于实验确定不规则形状物体的质量惯性矩极为有用的装置。它 由两块平行板组成,该平行板的整个装配体如同附加于竖直轴上的刚体那样作用着,而且它 的内部可以置放限于一定尺寸的任何物体。当它空着的时候(图4),此扭摆有一观察到的 周期t。当带着一个已知惯性矩为I:的物体与它一起振动时(图b),该摆的周期为下1,而 当带着未知帽性矩为1的物体时(图C),该摆以周期t2进行振动。试求出后一物体对旋转 轴线(亦即该轴的轴线)的惯性矩I。 。1=1瓷 (6) (c) 刘题1.2一2 1.2--3 一根重量为刚、长度为1的细 长棱柱形杆AB,A处为一铰,B处借一常数为 k的弹簧按水平状支承着,如图所示。试求该 杆在竖直平面内有一个很小的角位移值中时,复A 其旋转振动的周期。路去弹簧的质量,并考虑 杆是翔性的。 答: =2xV-3hg 习题1.2-3 1.2-4 一根重量为形、长度为【的细长刚性楼柱形杆AB,A处为铰接,借C处作 用竖直弹簧支承成水平位置(见图)。试求算该杆在竖直平面内有一微小旋转振幅时的周期·

假设弹簧常数为k,并略去质量不计。 答 习题1.2一4 习题1,2-5 1.2一5试确定阁中所示盘的扭转振动的频率。假设该轴的端点嵌固于A处和B处,轴 的两部分具有相同的直径d,但长度不同,为11和12。该盘的惯性矩为1。 答:∫=2V 3211112 1,2一6试确定一根直形轴的等效长度L1,该轴与图示曲柄轴的轴颈具有相同的扭转 刚度C1。曲柄连接板CE和D户的弯曲刚度为B。假设A和B处的轴承具有足够的空隙,允 许曲柄轴扭转过程中C和D自由侧向位移。曲柄插杆EF的扭转刚度为C2,摆幅半径为r。 答:Li=2a+8:6+2gr 12 习题1,2一6 习题1,2一7 1,2一7有两个平行轴AB和CD支承于轴承上,以齿轮衔接传动,如图所示。每一轴 的外端带有一个很重的盘,该系统进行扭转振动。试求算在下列数据时的振动周期:IA=I。 =10商-英寸-秒,1=:=60美寸,d=d:=3美寸,r,11=名。略去两个齿轮和两 根轴的惯量。假设每一轴的剪切模量G=12×10°磅/英寸2。 答:t芒0.158秒。 1.2一8再参见习题1.2一7中的系统,试求出与盘A和D相联结、直径为d,的单轴等 效长度L,的通式。 答:L=4(:)()°a