
4 总的振动,迟于图1,20中曲线所给 的运动分量,其角α称为这两种振动 的相差或相角。图1.3中坐标x, /p定义为相平面,在该平面内, sin pt 运动按转动向量处理。 例题1·一根长度1=10英尺、 A cos (pt -a) 弯曲刚度E1=20×108磅-类寸2的 简支钢梁,有一重量W=200磅的块 toc05p以 体从离度方=名英寸处落到跨中 上,如图1.4所示。略去梁的分布质 量,并假设在初始接触后,块体与梁 不分开,试求接着发生的自由振动的 频率和振幅。 解:在静止于梁中央处的荷载啊 图1.3 的作用下,其静力挠度为 6.=WIs (200)(120)3 48E7=748)20x10可=0.36英寸 因而,从方程(1.4),自由振动的频率为: 在求算振幅中,我们注意,当下落重量最初打击梁的初始时刻(=0),初始位移 为 x0=-8: 初始速度为: x。=1V2ga 因而,借方程(:),其振幅为: 4 A=V(-6t)+2n6=V0.13-0.36-V0.49=0.70英寸 因为此振幅是从静力平衡位置起度量,所以应看到,由于下落重量所产生的总挠度为A十8, =1.06英寸。 克2 (a) (8) 图 图1.5

例题2图1,5a中,重量为W的块体借两个串联的弹簧(它们的弹簧常数为k1和2) 吊挂着。图1.5b中,同一块体借两个所谓并联的弹簧(其常数为k,和k:)支承着。试对每 一种情况求出其系统的等效弹簧常数。 解:对于图1.5a中的情况,每一弹簧承受相同的拉力W,它们每一个的伸长量为81= W/k1和82=W/点2。因此,该重量的总的静力变位为: 6,=d,+da=+形 k:k2 该系统的等效弹簧常数为k=W18,,于是从方程(a),写成为: 1 质= (k) 将此值用于方程(1.3)中,我们可以求算自由振动的周期。 对于图1.5b中的情况,令S:为上面弹资中由于重量形静力作用所引起的拉力,S2为下 面弹簧所引起的压力。因为每一弹簧必定具有相同的长度变化,所以我们得到: d,==$=水 (1) 另外,该重量的单位变位产生的恢复力为:·~ k=k:十k2 (m) 它为该系统的等效弹簣常数。亦即,对于并联的弹簧,只需要将各别弹簧常数加起来,便得 到等效常数。各别弹簧中的力可从表达式(【)和(m)得到为: 51=,年” S2=R1+R2 (n) 例垂3一个简单框架结构,由重量W=38,600磅,借四根刚性竖宜柱支承着的刚性重 型平台组成,它的每一衡面内用两根对角钢丝侧面拉住,如图1.6a所示。诸柱端点均为铰 接,每一对角钢丝的横截面积为1/V2(英寸)2,张拉到很高的应力。除平台外,略去所 有的质蠹',试求出该结构自由侧向振动的周期π。 解:在平合的质量中心处顺x方向作用一力P,如图1.6五所示。由于此荷载,对角钢 丝AC中拉力的变化将为S=V2P/4。该对角钢丝的相应伸长量为: 4器=2- 4A2 2AE 对角钢丝BD缩短一个相等的量。由于对角钢丝的这些长度变化的结果,我们看到平台有一 侧向变位δ=V2d。因此,该结构的弹簧常数成为: P=V2AE=30×10 k= 120 -=250,000磅/类寸 将此k值代人方程(1.3),我们得到: T=27V 38,600 (250,000)(386) =2πV0.0004=0.126秒 留给读者去说明在此例题中不一定需要顺x方向作用水平力P,如果P顺2方向或顺水平面 内任何其它方向,将得到相同的结果。 *即略去诸柱和钢丝的质量。 一译注
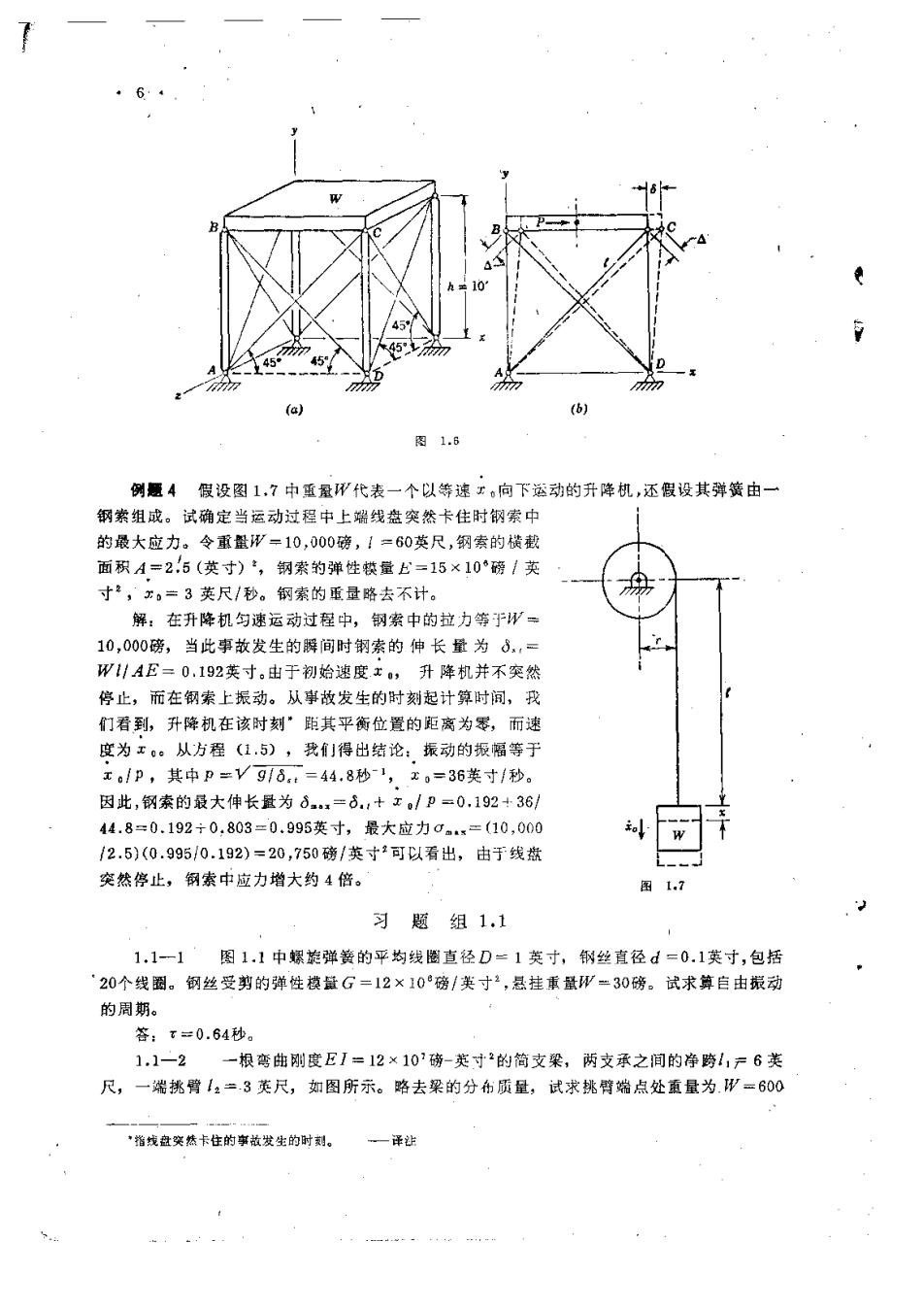
5 70 n形 (a) (b) 图1.6 例题4假设图1,7中重量形代表一个以等速工。向下运动的升降机,还假设其弹簧由一 钢索组成。试确定当运动过程中上端线盘突然卡住时钢索中 的最大应力。令重量形=10,000磅,1=60英尺,钢索的横截 面积A=2.5(英寸)·,钢索的弹性轶童上=15×10磅1英 寸,x,=3英尺/秒。钢索的重量略去不计。 解:在开降机匀速运动过程中,钢索中的拉力等于W= 10,000磅,当此事故发生的瞬间时钢索的伸长量为8.,一 W1/AE=0.192英寸。由于初始速度x。,升降机并不突然 停止,而在钢索上振动。从事故发生的时刻起计算时间,我 们看到,升降机在该时刻”距其平衡位置的距离为零,而速 度为x。从方程(1.5),我」得出结论:振动的振幅等于 x。/p,其中p=V96:=44.8秒1,x。=36英寸/秒。 因此,钢索的最大伸长量为6.x=6,+x。/p=0,192+36 44.8=0.192÷0,803=0.995英寸,最大应力0m.x=(10,000 /2.5)(0.995/0.192)=20,750磅/英寸可以看出,由于线盘 突然停止,钢索中应力增大约4倍。 图1.7 习题组1.1 1.1-一1图1.1中螺旋弹簧的平均线圈直径D二1英寸,钢丝直径d=0.1英寸,包括 20个线圈。钢丝受剪的弹性模量G=12×10°磅/类寸2,悬挂重量形=30磅。试求算自由擐动 的周期。 答:T=0.64秒。 1.1一2一根弯曲刚度EI=12×10?磅-英寸2的简支梁,两支承之间的净跨11示6芙 尺,一端挑臂I2=.3英尺,如图所示。路去梁的分布质量,试求挑臂端点处重量为.形=600 指线盘突然卡住的事放发生的时刻。 一译泸
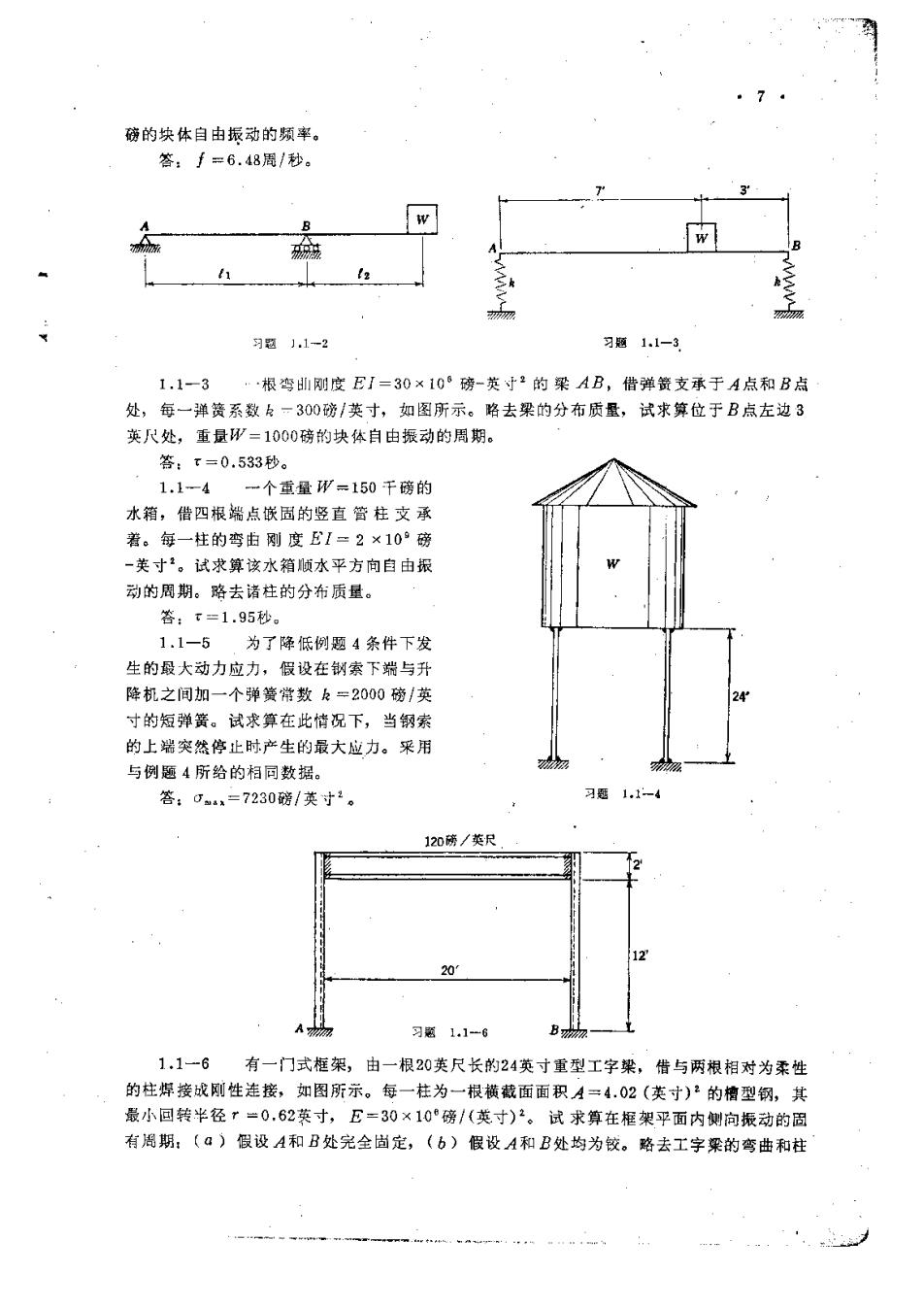
磅的块体自由振动的频率。 答:手=6.48周/秒。 B 习题J.1-2 习题1.1-3 1.1一3·根弯刚度EI=30×108磅-英寸2的梁AB,借弹簧支承于A点和B点 处,每一弹簧系数k一300磅/英寸,如图所示。略去梁的分布质量,试求算位于B点左边3 英尺处,重量W=1000磅的块体自由振动的周期。 答:T=0.533秒。 1.1一4一个重量W=150千磅的 水箱,借四根端点嵌固的竖直管柱支承 着。每一柱的弯由刚度E1=2×10°磅 -美寸2。试求算该水箱顺水平方向自由报 动的周期。略去诸柱的分布质量。 答:t=1.95秒。 1.1一5为了降低例题4条件下发 生的最大动力应力,假设在钢索下端与升 降机之间加一个弹簧常数k=2000磅/英 寸的短弹簧。试求算在此情况下,当钢索 的上端突然停止时产生的最大应力。采用 与例题4所给的相同数据。 答:0a.=7230磅/英寸2。 习题1.1-4 120磅/英尺 201 习题1.1-6 B 1.1一6有一门式框架,由一根20英尺长的24英寸重型工字梁,借与两根相对为柔性 的柱焊接成刚性连接,如图所示。每一柱为一根横截面面积A=4.02(英寸)2的槽型钢,其 最小回转半径r=0.62英寸,E=30×10°磅/(英寸)2。试求算在框架乎面内侧向振动的周 有周期:〔a)假设A和B处完全固定,(b)假设A和B处均为铰。略去工字梁的弯曲和柱
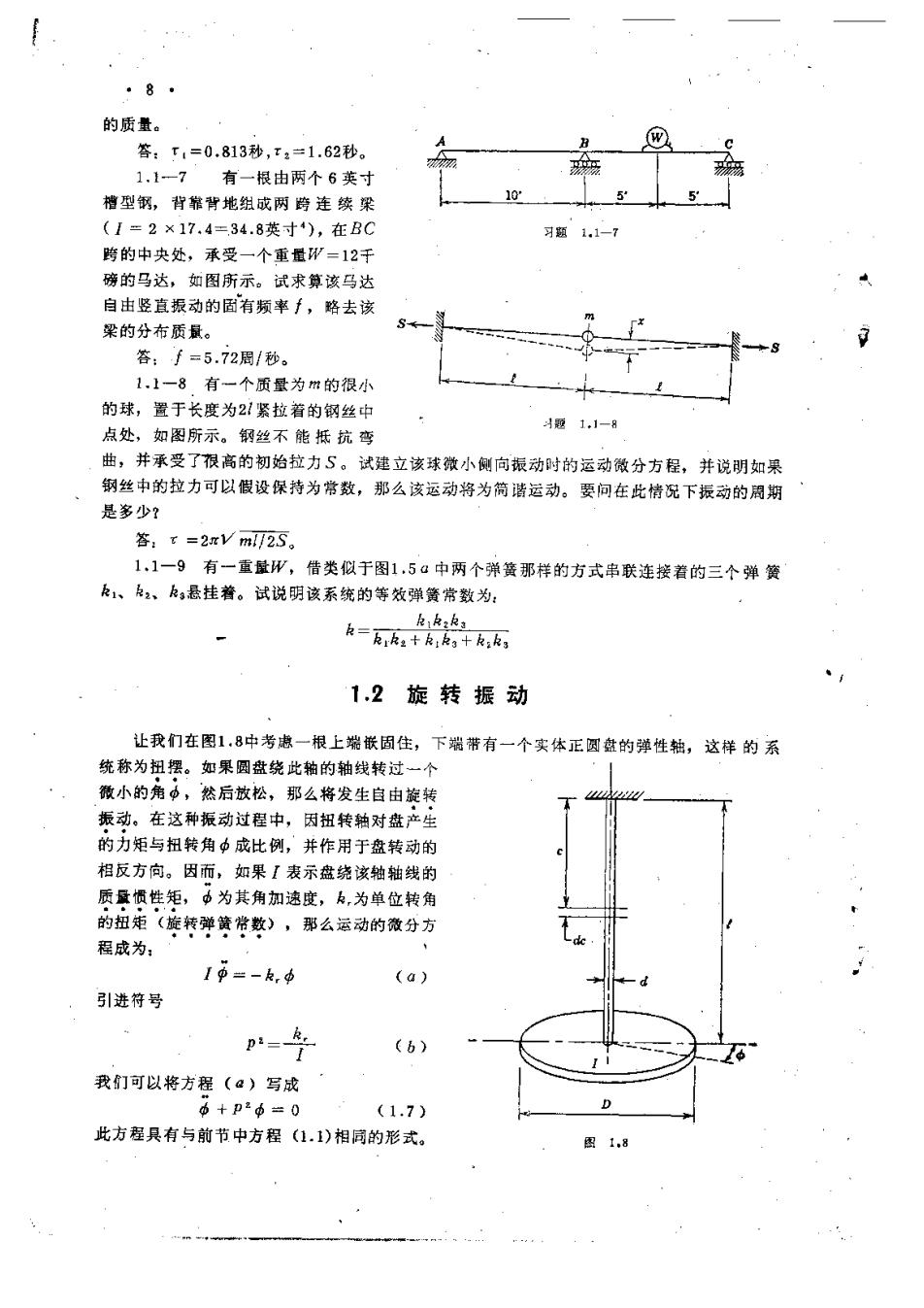
·8 的质量。 答:,=0.813秒,t2=1.62秒。 1.1一7有一根由两个6英寸 槽型钢,背靠背地组成两跨连续梁 5 (1=2×17.4=34.8英寸4),在BC 习题1,1-7 跨的中央处,承受一个重量形=12于 磅的马达,如图所示。试求算该马达 自由竖直振动的固有频率手,略去该 梁的分布质晟。 答:f=5.72周/秒。 1.1一8有一个质量为m的很小 的球,置于长度为2!紧拉着的钢丝中 以题1.1一8 点处,如图所示。钢丝不能抵抗弯 曲,并承受了很高的初始拉力S。试建立该球微小侧向振动时的运动微分方程,并说明如果 钢丝中的拉力可以假设保持为常数,那么该运动将为筒谐运动。要问在此情况下振动的周期 是多少? 答:t=2rVm/2S。 1.1一9有一重量W,借类似于图1.5a中两个弹簧那样的方式串联连接着的三个弹簧 k1、2、k,悬挂着。试说明该系统的等效弹簧常数为: kk2k3 克=Rk2tR,,+k,k 1.2旋转振动 让我们在图1.8中考虑一根上端嵌固住,下端带有一个实体正圆盘的弹性轴,这样的系 统称为扭摆。如果圆盘绕此轴的轴线转过一个 微小的角中,然后放松,那么将发生自由旋转 振动。在这种振动过程中,因扭转轴对盘产生 的力矩与扭转角中成比例,并作用于盘转动的 相反方向。因而,如果【表示盘绕该轴轴线的 质量惯性矩,中为其角加速度,k,为单位转角 的扭矩(旋转弹簧常数),那么运动的微分方 程成为: I中=-k,中 (a) 引进符号 p:=k (6) 我们可以将方程(a)写成 6+卫2中=0 (1.7) D 此方程具有与前节中方程(1.1)相同的形式。 图1.8