
2021-12-28 《数学建模》课件汇总 海 境模范例:人口模型 ⊙ 据人口学掌们上世纪求预测,则2033年世界人口将突或100亿 每年增加近1亿人口,以后还会远徒增长。人们开始考意我们横 以生卉的地球究竟能否承变如此的增长。 且全球各地区人口变化如下: 非洲地区人口将从10.33亿增至19.85亿: 欧洲人口将从7.33亿减至6.91亿 2.4人口模型 增幅藏大亚浏地区的人口将从41.67亿增至52.32亿。 中自人口晴态何变他? 中国的人口变化引起了很多人的关注,人口藏策也在发 问通1形响1时刻某地区的人口总数变化的最显著因素应包 生藏变,多种观燕相互碰撞,甚至是冲变的,如何恶考这 括哪些7 形响明章 些问题? 个体的出生 新 + 凄流建立人口预测数学模型 问题2这里准备考感哪些因素? 讨论最筒草的情况,仗考意出生和死亡对人口 变化的彩响。 问通3用什么变量描述人口变化情况? 银设 时间间隔△内的出生人戴△N:△N=bN(g 人世藏意 人口德教 ·时间间隔△内的死亡人数△N2:△N=dN)△ 2.意立敏学模型 假定b>0,d>0,从而在时间区闲△内,有 设1时刘一个地区的人口总数为N(0 N(+△)-N0=AN1-△N2=(b-d)N(△M 业分模型 问题3在时闻:比,什△内出生和死亡所藏人口数壹变化与哪 即 N什△)N④=(b-dN(M (1) 些变量有关? 1)出生率和元亡单: 将人口数N)礼为一个连峡可乎变量,在很维的时间区间 2)时闲筒属AM的关短 △山内,则方狂(1)敌写为 3)初始时刻1=0时的人口基教。 第16页,共105页
2021-12-28 1 1 2.4 人口模型 2 据人口学家们上世纪末预测 , 到2033年世界人口将突破 100亿, 每年增加近1亿人口, 以后还会迅猛增长。人们开始考虑我们赖 以生存的地球究竟能 否承受如此的增长。 建模范例:人口模型 且全球各地区人口变化如下: 非洲地区人口将从 10.33亿增至19.85亿; 欧洲人口将从 7.33亿减至6.91亿; 增幅最大亚洲地区的人口将从 41.67亿增至52.32亿。 中国人口将如何变化? 3 尝试建立人口预测数学模型 . 中国的人口变化引起了很多人的关注,人口政策也在发 生改变,多种观点相互碰撞,甚至是冲突的,如何思考这 些问题? 4 影响因素 个 体 的 出 生 、 死 亡 迁 入 迁 出 年 龄 结 构 性 别 比 例 …… 教 育 程 度 当 地 经 济 生 育 观 念 问题1 影响 t 时刻某地区的人口总数变化的 最显著因素应包 括哪些? 讨论最简单的情况,仅考虑 出生和死亡对人口 变化的影响。 问题2 这里准备考虑哪些因素? 5 设 t 时刻一个地区的人口总数为 N(t) . 问题3 在时间段[t, t+ t] 内出生和死亡所致人口数量变化与哪 些变量有关? 2.建立数学模型 2)时间间隔t 的长短; 3)初始时刻t = 0时的人口基数。 1)出生率和死亡率; 问题3 用什么变量描述人口变化情况? 人口密度 人口总数 ? 6 假设 l 时间间隔t内的出生人数 N1: N(t+t)N(t) l 时间间隔t内的死亡人数 N2: 则方程(1)改写为 将人口数N(t)视为一个连续可导 变量, 在很短的时间区间 假定b>0, d > 0,从而在时间区间t内,有 =N1 - N2 差分模型 (1) = (bd)N (t) t 即 N(t+t)N(t) = (bd)N (t) t N1= b N(t)t; N2=d N(t)t. t内, 《数学建模》课件汇总 第16页,共105页
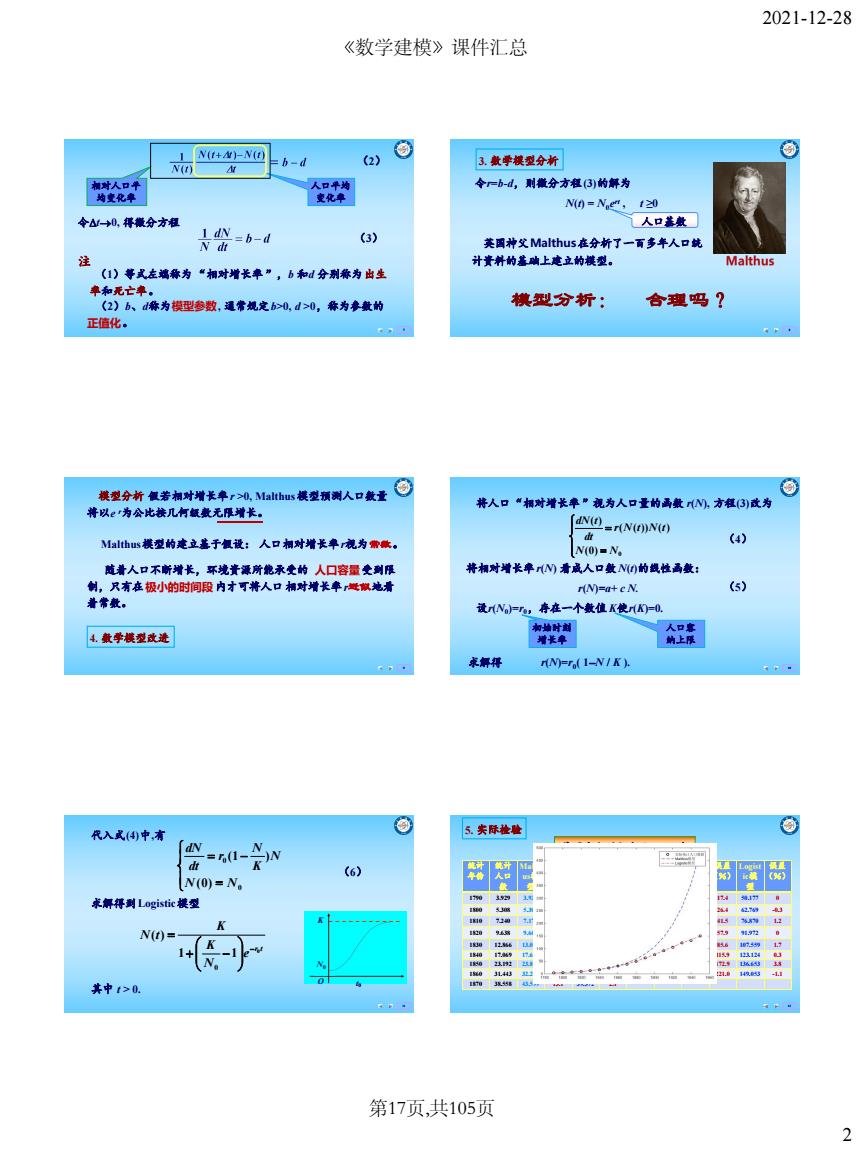
2021-12-28 《数学建模》课件汇总 1 N(t+A)-N(t N() b-d (2) 3.数季模型分析 相树人口 人口平均 令=b-d,则撒分方在(3)的解为 均变化率 变化率 N0=Ne",t20 令△1+0,得撒分方和 人口基数 1dV=b-d (3) N dt 英国神父Malthus在分新了一百多年人口能 注 计资并的基响上遮立的模型。 Malthus (1)号式左鸿春为“相对增长率”,b和山分别兼为出生 来和死亡来。 (2)b、d桥为模型参数,通常规定b>0,d>0,希为◆戴的 模型分析: 合理吗? 正值化, 模型分析假若相对增长率r>0,Malthus楼型预测人口教量 将人口“相对增长率”视为人口量的高数N),方在3)改为 将以e‘为公比按几有额戴无厚增长。 NO=rNeN四 falthus模型的建立基于根设:人口相对增长r视为康黛。 (4) N(0)▣W 随着人口不断增长,环境贵漂所能承变的人口容量变到限 将相对增长率W)看成人口数N的线性画数: 制,只有在极小的时间殿内才可将人口桶对增长事:地青 r(N)=a+c N. (5) 着常数。 设N0=可,存在一个戴值K使r瓜=0. 人口 4.数学模型改进 州长率 钠上及 求解得 r(N)=r(1-N/K ) 代入式)中,有 5.失际检整 dN =(1- N )N (6) N(0)=N。 求解得到Logistic模型 170 1 74 N(t)= 1+ EEEE 4 其中>0. 55 5 第17页,共105页 2
2021-12-28 2 7 人口平均 变化率 相对人口平 均变化率 令t0, 得微分方程 (3) (1)等式左端称为 “相对增长率”,b 和d 分别称为出生 率和死亡率。 (2)b、d称为模型参数, 通常规定b>0, d >0,称为参数的 正值化。 注 (2) 8 3. 数学模型分析 N(t) = N0e rt , t ≥0 人口基数 英国神父Malthus在分析了一百多年人口统 计资料的基础上建立的模型。 令r=b-d,则微分方程(3)的解为 模型分析: 合理吗? 9 模型分析 假若相对增长率r >0, Malthus模型预测人口数量 将以e r为公比按几何级数无限增长。 Malthus模型的建立基于假设: 人口相对增长率r视为常数。 随着人口不断增长,环境资源所能承受的 人口容量受到限 制,只有在极小的时间段 内才可将人口 相对增长率r近似地看 着常数。 4. 数学模型改进 10 将人口“相对增长率”视为人口量的函数 r(N), 方程(3)改为 (4) 将相对增长率r(N) 看成人口数N(t)的线性函数: 设r(N0)=r0,存在一个数值 K使r(K)=0. 初始时刻 增长率 人口容 纳上限 求解得 r(N)=r0( 1N / K ). 0 (0) ( ( )) ( ) ( ) N N r N t N t dt dN t r(N)=a+ c N. (5) 11 代入式(4)中,有 0 0 (0) (1 ) N N N K N r dt dN (6) 求解得到Logistic模型 其中 t > 0. t0 O N0 K r t e N K K N t 0 1 1 ( ) 0 12 统计 年份 统计 人口 数 Malth us模 型 误差 (%) Logist ic模 型 误差 (%) 统计 年份 统计 人口 数 Malth us模 型 误差 (%) Logist ic模 型 误差 (%) 1790 3.929 3.929 0 3.929 0 1880 50.156 58.901 17.4 50.177 0 1800 5.308 5.308 0 5.336 0.5 1890 62.948 79.574 26.4 62.769 -0.3 1810 7.240 7.171 -0.9 7.228 -0.2 1900 75.995 107.503 41.5 76.870 1.2 1820 9.638 9.668 0.5 9.757 1.2 1910 91.972 145.234 57.9 91.972 0 1830 12.866 13.088 1.7 13.109 1.9 1920 105.711 196.208 85.6 107.559 1.7 1840 17.069 17.682 3.6 17.506 2.6 1930 122.775 265.074 115.9 123.124 0.3 1850 23.192 23.888 3.0 23.192 0 1940 131.669 358.109 172.9 136.653 3.8 1860 31.443 32.272 2.6 30.412 -3.3 1950 150.697 483.798 221.0 149.053 -1.1 1870 38.558 43.599 13.1 39.372 2.1 美国十九世纪初人口预测 5. 实际检验 《数学建模》课件汇总 第17页,共105页

2021-12-28 《数学建模》课件汇总 6.总地 @ ●不同的人,出发点不同,摸型可能不同: ·建模过准不是一次性戴建好,是个不晰禄素过准: ●通常需要利用一些怡当的银设来 简化问题。 第18页,共105页 3
2021-12-28 3 13 6. 总结 l 不同的人,出发点不同,模型可能不同; l 建模过程不是一次性就建好,是个不断探索过程 ; l 通常需要利用一些恰当的假设来 简化问题。 《数学建模》课件汇总 第18页,共105页
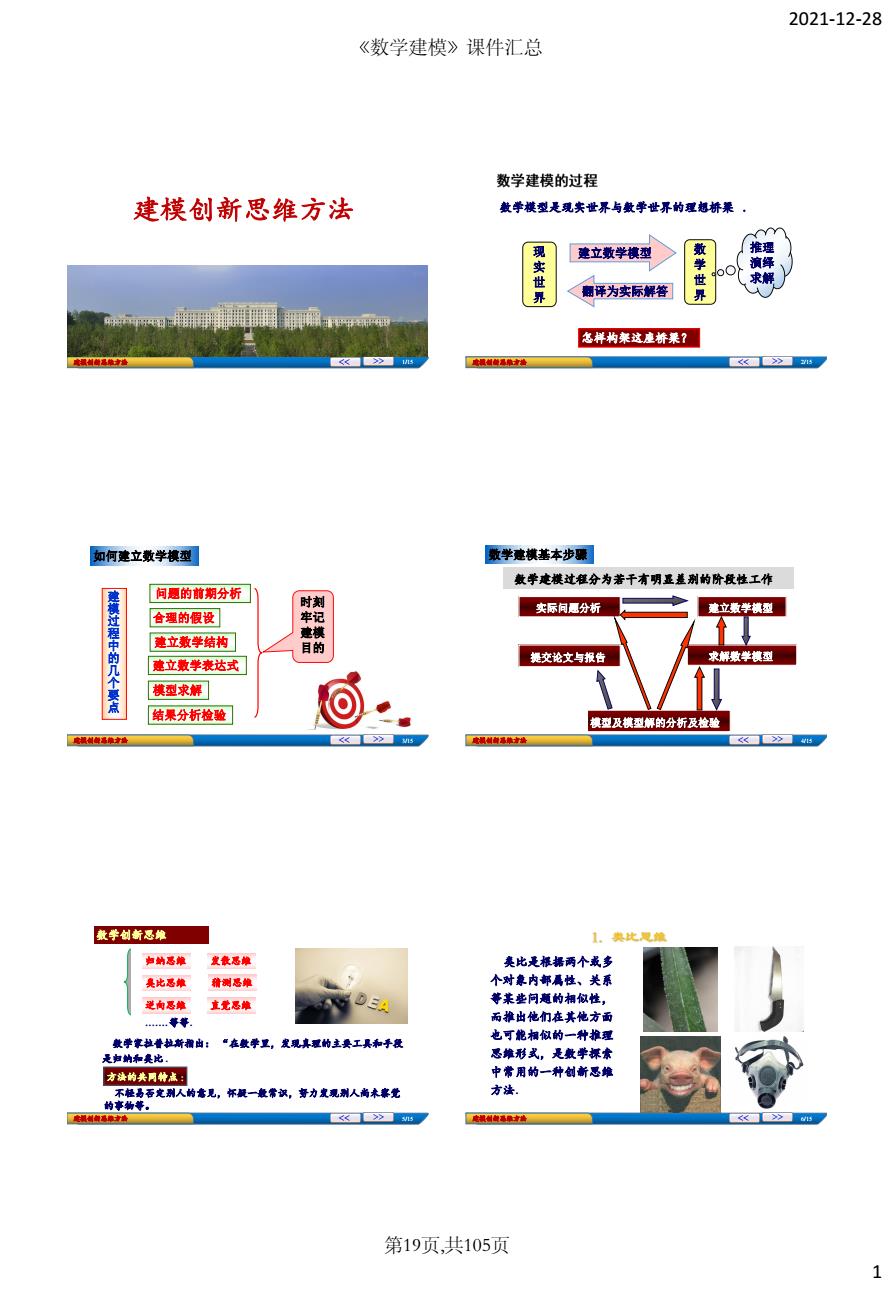
2021-12-28 《数学建模》课件汇总 数学建模的过程 建模创新思维方法 数学模型是现实世界与数学世界的理想桥果, 建立数学模型 推理 实世界 学世 滴绎 求解 翻译为实际解答 怎样构来这座桥果? 动银训的⅓中地 <》4 如何建立数学模型 数学建棋基本步漂 数学建模过稚分为若千有明显差别的阶段性工作 问题的前期分析 时 实际问愿分析 建立数学镇型 模过程中的几个要 合理的假设 牢记 建立教学结构 建模 建立数学表达式 是交论文与报告 求解敷学摸型 模型求解 结果分析检验 模型及棋型解的分析及检验 <》 数学创奇忌燥 1。典比见第 声钠惑单 发表恐维 爽比是根据两个或多 是比恶维 精测忌维 个对兼内部属性、关系 逆向总维 直觉悬雄 DEA 等某些问题的相似性, 而推出他们在其他方面 也可能相似的一种推理 数学掌拉普拉新稻山: “在数学卫,发现具覆的主要工具布手没 是归钠和是比 忌蜂形式,是数学探素 方法的共同种法: 中常用的一种创新思堆 不轻否别人的意见,怀一最常议,誓力发观别人尚术觉 方法 的事物普。 老钢制物路原立★一 <<>》s 电银制期单典 第19页,共105页 1
2021-12-28 1 建模创新思维方法 1/15 建模创新思维方法 建模创新思维方法 2/15 现 实 世 界 数 学 世 界 建立数学模型 推理 演绎 求解 翻译为实际解答 数学模型是现实世界与数学世界的理想桥梁 . 怎样构架这座桥梁? 建模创新思维方法 3/15 建 模 过 程 中 的 几 个 要 点 问题的前期分析 合理的假设 建立数学表达式 建立数学结构 时刻 牢记 建模 目的 如何建立数学模型 模型求解 结果分析检验 建模创新思维方法 4/15 数学建模过程分为若干有明显差别的阶段性工作 求解数学模型 实际问题分析 建立数学模型 提交论文与报告 模型及模型解的分析及检验 数学建模基本步骤 建模创新思维方法 5/15 数学创新思维 …….等等. 类比思维 归纳思维 逆向思维 发散思维 猜测思维 直觉思维 数学家拉普拉斯指出: “在数学里,发现真理的主要工具和手段 是归纳和类比 . 方法的共同特点 : 不轻易否定别人的意见,怀疑一般常识,努力发现别人尚未察觉 的事物等。 建模创新思维方法 6/15 类比是根据两个或多 个对象内部属性、关系 等某些问题的相似性, 而推出他们在其他方面 也可能相似的一种推理 思维形式,是数学探索 中常用的一种创新思维 方法. 《数学建模》课件汇总 第19页,共105页

2021-12-28 《数学建模》课件汇总 典比是维的几个特康 如阿具高典比站论的可意性 1是比是从人们已经掌握了的事物的属性,推测正在研究的事物的属 第一,臭比对厚的相同4性婚多,则结论的可靠性婚大;例 如:为了提高荡物清效,在给病人服用前,要在小动物身上做 丝,是以旧有的认识为盖确,臭比出新的姑果。 一最都用小白真来迹行就脸,小白氯和人有不少的共同 之处 加果在小动物上有效,那么,在人身上也可能有 2臭比是从一种事物的特豫具性护测另 定疗 一种事物的特殊属社。 3.臭比的帖果是精测性的不一安案 位它脚有发现的动能 鸡织创的洛格立油 <>ws 动银创外中语 <》4 如何镇高典比结论的可售 是比的湘同属性魏是童要的、本质的,韩论的可靠世 幕三,类比的相 蕾切,这种联系的: 更斯把光和声两是对进行臭比, 具有 茶楼行指华麦垫新子 扰的现象等。 斋辛,醉 而声是由一种周期运功所引起的,里波动状态:由此,悬更 斯提出丁光也里流动状毒的理论。 李四光研究了中亚朝亚的地 质结构,发现中亚细亚的地质 情况与中图的松过平原的地质 塘构板其相似,从而推断出松 过平原也象中亚解亚那样蕴薰 青石油。 典比见雄的形成 对手机销售问题的分析: 类比忌维的常见形式有: 1)一最奉人只需用 (2)南期在广香之夹推 形式典比:如飞机每高臭、飞机与靖展,狗式上接本。 1一2个手机就是够,一个 馆作用下售速度快,南 功能类比:加各种机城平、辱业夹普。 地区的富求量是有限的: 品地于他和时铺鲁速成会 幻规类比:根据为越中的来种形象、某种作用、运动兼重逢行观 明造悬雄。 方法类比:利用臭似的方裤逢杆处夏。 手机竹前售情况类似于人口增长情况,可利用夹比方法建立提型 例21新产品铺摸型 L0 gistie模型特点潮期高速增长, 怎押建立一个数学援型精远新产品(斗机)推铺速度,并由此分斯山 过一个补定时同底唇增长速度减城,N()= 一些有用的姑果以霜导生产, 且有上界控的 1+Ce>0 想一想此问瓶与序个走模网燕湘臭似? 底钢制物路原★一 <>》n 电银制酸路墙 <<》n: 第20页,共105页 2
2021-12-28 2 建模创新思维方法 7/15 1.类比是从人们 已经掌握了的事物的属性, 推测正在研究 的事物的属 性,是以旧有的认识为基础,类比出 新的结果. 2.类比是从一种事物的特殊属性推测 另 一种事物的特殊属性 . 3.类比的结果是猜测性的 , 但它却有发现的功能. 建模创新思维方法 8/15 第一,类比对象的 相同属性越多 ,则结论的 可靠性越大 ;例 如:为了提高药物疗效,在给病人服用前,要在小动物身上做 试验,一般都用小白鼠来进行试验,小白鼠和人有不少的共同 之处。如果在小动物身上有疗效,那么,在人身上也可能有一 定疗效。 建模创新思维方法 9/15 第二,类比的相同属性 越是重要 的、本质的,结论的 可靠性 就越大。例如: 惠更斯把光和声两类对象进行类比,在类比中抓住了它们之 间具有一系列本质相同的属性:直线传播,有反射、折射和干 扰的现象等。 而声是由一种周期运动所引起的,呈波动状态;由此,惠更 斯提出了光也呈波动状态的理论。 建模创新思维方法 10/15 第三,类比的相同属性与推出属性之间彼此的联系越 密切,这种联系的相关程度越高,则结论的可靠性就越 大。例如: 1922年,美国斯坦福大学教授布莱克威尔德 调查了中国,给了一顶 “贫油”的帽子。 李四光研究了中亚细亚 的地 质结构,发现中亚细亚的地质 情况与中国的松辽平原的地质 结构极其相似,从而推断出 松 辽平原也象中亚细亚那样蕴藏 着石油。 建模创新思维方法 11/15 类比思维的常见形式有: 怎样建立一个数学模型描述新产品 (手机)推销速度,并由此分析出 一些有用的结果以指导生产 . 例2.1 新产品销售模型 想一想 此问题与哪个建模问题相类似? :如飞机与鸟类、飞机与蜻蜒,狗爬式上楼车。 :如各种机械手、鳄鱼夹等。 :根据幻想中的某种形象、某种作用、运动装置进行发 明创造思维。 :利用类似的方法进行处理。 建模创新思维方法 12/15 (1) 一般每人只需用 1~2个手机就足够 ,一个 地区的需求量是有限的; 手机的销售情况类似于人口增长情况,可利用类比方法建立模型 . (2) 初期在广告之类推 销作用下销售速度较快 ,商 品趋于饱和时销售速度会 减缓. Logistic 模型特点 初期高速增长, 过一个特定时间点后增长速度减缓, 且有上界控制 . ( ) , 0 1 N t t St CeK 《数学建模》课件汇总 第20页,共105页