
教师 教 案 课程名称:漫话数学建模 课学时:32 课程组所在学院:数学科学学院
教 师 教 案 课 程 名 称:漫话数学建模 课 学 时:32 课程组所在学院:数学科学学院
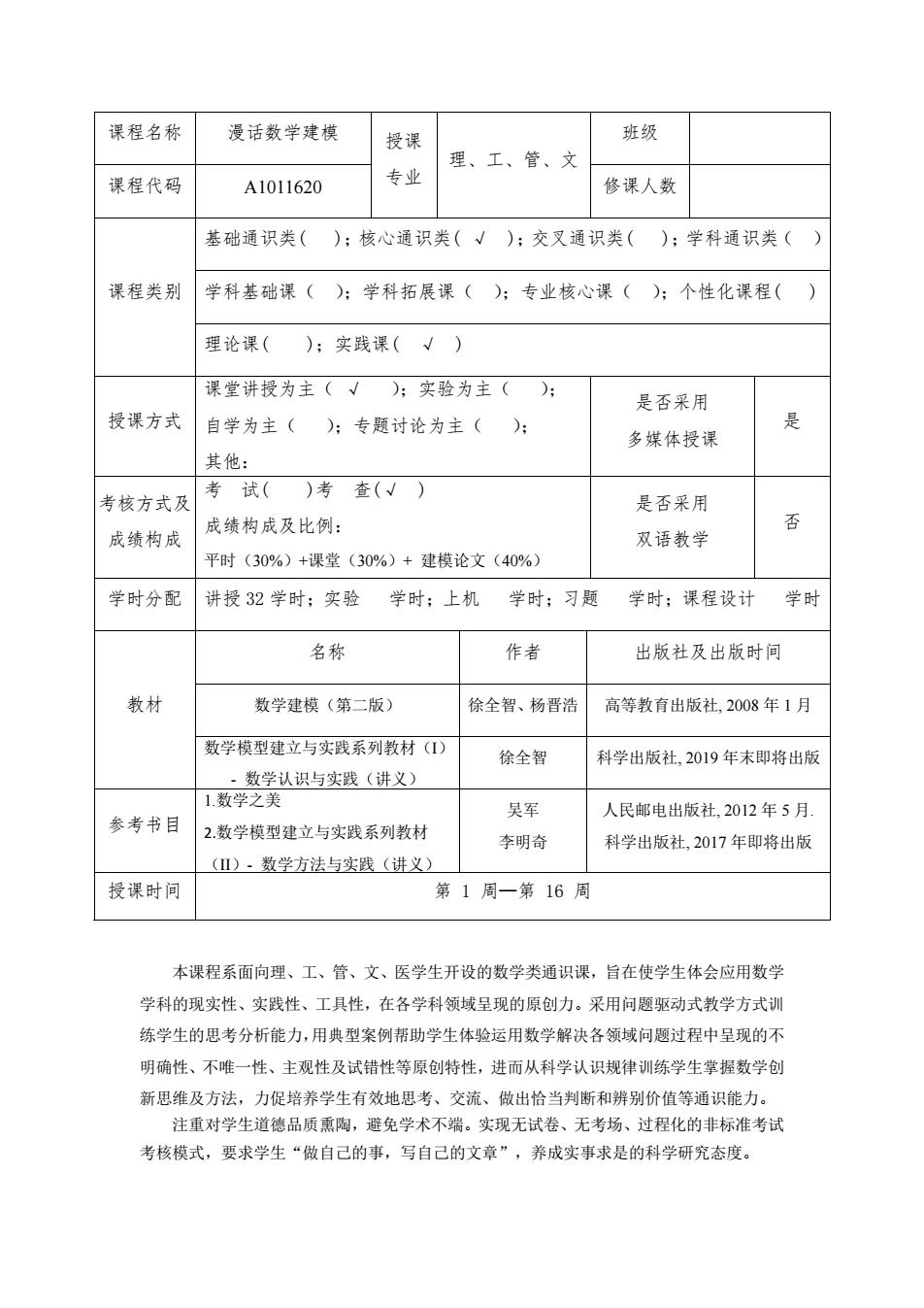
课程名称 漫话数学建模 授课 班级 理、工、管、文 课程代码 A1011620 专业 修课人数 基础通识类():核心通识类(√);交叉通识类( ):学科通识类() 课程类别 学科基础课():学科拓展课():专业核心课():个性化课程() 理论课( );实践课(√) 课堂讲授为主(√):实验为主(): 是否采用 授课方式 自学为主():专题讨论为主(): 是 多媒体授课 其他: 考试( )考查(√) 考核方式及 是否采用 成绩构成及比例: 否 成绩构成 双语教学 平时(30%)+课堂(30%)+建模论文(40%) 学时分配 讲授32学时;实验 学时:上机 学时;习题 学时;课程设计 学时 名称 作者 出版社及出版时间 教材 数学建模(第二版) 徐全智、杨晋浩 高等教育出版社,2008年1月 数学模型建立与实践系列教材() 徐全智 科学出版社,2019年末即将出版 ·数学认识与实践(讲义) 1.数学之美 吴军 人民邮电出版社,2012年5月 参考书目 2.数学模型建立与实践系列教材 李明奇 科学出版社,2017年即将出版 ()·数学方法与实践(讲义) 授课时间 第1周一第16周 本课程系面向理、工、管、文、医学生开设的数学类通识课,旨在使学生体会应用数学 学科的现实性、实践性、工具性,在各学科领域呈现的原创力。采用问题驱动式教学方式训 练学生的思考分析能力,用典型案例帮助学生体验运用数学解决各领域问题过程中呈现的不 明确性、不唯一性、主观性及试错性等原创特性,进而从科学认识规律训练学生掌握数学创 新思维及方法,力促培养学生有效地思考、交流、做出恰当判断和辨别价值等通识能力。 注重对学生道德品质熏陶,避免学术不端。实现无试卷、无考场、过程化的非标准考试 考核模式,要求学生“做自己的事,写自己的文章”,养成实事求是的科学研究态度
课程名称 漫话数学建模 授课 专业 理、工、管、文 班级 课程代码 A1011620 修课人数 课程类别 基础通识类( );核心通识类( √ );交叉通识类( );学科通识类( ) 学科基础课( );学科拓展课( );专业核心课( );个性化课程( ) 理论课( );实践课( √ ) 授课方式 课堂讲授为主( √ );实验为主( ); 自学为主( );专题讨论为主( ); 其他: 是否采用 多媒体授课 是 考核方式及 成绩构成 考 试( )考 查(√ ) 成绩构成及比例: 平时(30%)+课堂(30%)+ 建模论文(40%) 是否采用 双语教学 否 学时分配 讲授 32 学时;实验 学时;上机 学时;习题 学时;课程设计 学时 教材 名称 作者 出版社及出版时间 数学建模(第二版) 徐全智、杨晋浩 高等教育出版社, 2008 年 1 月 数学模型建立与实践系列教材(I) - 数学认识与实践(讲义) 徐全智 科学出版社, 2019 年末即将出版 参考书目 1.数学之美 2.数学模型建立与实践系列教材 (II)- 数学方法与实践(讲义) 吴军 李明奇 人民邮电出版社, 2012 年 5 月. 科学出版社, 2017 年即将出版 授课时间 第 1 周—第 16 周 本课程系面向理、工、管、文、医学生开设的数学类通识课,旨在使学生体会应用数学 学科的现实性、实践性、工具性,在各学科领域呈现的原创力。采用问题驱动式教学方式训 练学生的思考分析能力,用典型案例帮助学生体验运用数学解决各领域问题过程中呈现的不 明确性、不唯一性、主观性及试错性等原创特性,进而从科学认识规律训练学生掌握数学创 新思维及方法,力促培养学生有效地思考、交流、做出恰当判断和辨别价值等通识能力。 注重对学生道德品质熏陶,避免学术不端。实现无试卷、无考场、过程化的非标准考试 考核模式,要求学生“做自己的事,写自己的文章”,养成实事求是的科学研究态度

充分发挥本课程特点,合理有效应用典型案例,将“课程思政”融入课堂内外及各教学 环节,培养学生运用数学于各类科学技术领域,形成解决复杂问题能力,突出培育求真务实、 实践创新、精益求精的工匠精神,锤炼学生踏实严谨、耐心专注、吃苦耐劳、追求卓越等优 秀品质,成长为心系社会、有时代担当的专业人才。 第一章 序言 一、教学内容及要求(4学时) 认知数学的科学性及应用性,了解数学的文化性、工具性及技术性,了解本课程教学的 实践性,了解教学目标、教学理念及教学方法 二、教学重点、难点及解决办法 转变学生视数学学习等同“做习题”的学习观念,引导学生尝试从新的角度去了解数 学,认知数学,激发学生学习数学的兴趣 三、教学设计 1设计以下问题与学生共同讨论,帮助学生对自己的数学认知、学习理念、学习方法开 始有所反省,提高眼界,培养审视、分析问题的大格局、大视野 1)数学是什么? 2)数学就在那里,你在哪里? 3)你心目中的数学? 4)你热爱数学吗? 5)中国有西海吗?蜘蛛有奶吗? 2.通过“创意平板折叠桌”等案例的介绍,开拓学生对数学的工具性、技术性及应用 性的视野」 3.通过对陈省身、杨振宁、林家翘等数学物理大师的工作简介,帮助学生认知数学学科, 加深拓展学生对数学的认识及理解, 4.通过“月上柳梢头,人约黄昏后”、“仰望星空,满天繁星”等小案例,了解数学的 文化性,思维训练的有效性,提高对实际问题的认知能力:利用案例“大夫的决策”使学生 理解“数学是一种科学语言”.在案例讨论与学习中体现课程思政的发展逻辑分析思辨能力, 增强理论自信和文化自信,逐渐培养学生能够形成观点、诠释观点等方面的听说读写“新四 会”能力 课程序言预期达到教学效果,使学生深刻理解以下论述: “从认识论的观点来看,人们应该给数学科学以无上的地位.”一一J勒雷 “自然界的事物基本上都很简单,所有的基础原理及主要问题都可以用数学方式表达
充分发挥本课程特点,合理有效应用典型案例,将“课程思政”融入课堂内外及各教学 环节,培养学生运用数学于各类科学技术领域,形成解决复杂问题能力,突出培育求真务实、 实践创新、精益求精的工匠精神,锤炼学生踏实严谨、耐心专注、吃苦耐劳、追求卓越等优 秀品质,成长为心系社会、有时代担当的专业人才。 第一章 序言 一、教学内容及要求(4 学时) 认知数学的科学性及应用性, 了解数学的文化性、工具性及技术性, 了解本课程教学的 实践性, 了解教学目标、教学理念及教学方法. 二、教学重点、难点及解决办法 转变学生视数学学习等同“做习题”的学习观念, 引导学生尝试从新的角度去了解数 学, 认知数学, 激发学生学习数学的兴趣. 三、教学设计 1.设计以下问题与学生共同讨论, 帮助学生对自己的数学认知、学习理念、学习方法开 始有所反省, 提高眼界, 培养审视、分析问题的大格局、大视野. 1) 数学是什么? 2) 数学就在那里, 你在哪里? 3) 你心目中的数学? 4) 你热爱数学吗? 5) 中国有西海吗?蜘蛛有奶吗? 2. 通过 “创意平板折叠桌”等案例的介绍, 开拓学生对数学的工具性、技术性及应用 性的视野. 3. 通过对陈省身、杨振宁、林家翘等数学物理大师的工作简介, 帮助学生认知数学学科, 加深拓展学生对数学的认识及理解. 4. 通过“月上柳梢头, 人约黄昏后”、 “仰望星空, 满天繁星”等小案例, 了解数学的 文化性, 思维训练的有效性, 提高对实际问题的认知能力;利用案例“大夫的决策”使学生 理解“数学是一种科学语言”. 在案例讨论与学习中体现课程思政的发展逻辑分析思辨能力, 增强理论自信和文化自信, 逐渐培养学生能够形成观点、诠释观点等方面的听说读写“新四 会”能力. 课程序言预期达到教学效果, 使学生深刻理解以下论述: “从认识论的观点来看, 人们应该给数学科学以无上的地位.” ——J.勒雷 “自然界的事物基本上都很简单, 所有的基础原理及主要问题都可以用数学方式表达

这是一个应用数学家的信仰.”一应用数学大师林家翘 第二章数学的应用 一、教学内容及要求(6学时) 了解数学的抽象性和逻辑性;了解数学研究对象的多样性与内部的统一性;了解数学应 用的广泛性与描述的精确性.了解应用数学过程的五个阶段性工作:识别和剖析问题、提取数 学结构、描述数学问题、科学计算、解释评判结论 二、教学重点、难点及解决办法 学习数学理论知识与应用数学有极大差异,需转变学生的学习理念和学习方法建模过 程的五个阶段性工作是应用数学的重要环节,且涉及到对数学的全面认知,仅依靠老师抽象 讲授学生很难理解,选择恰当的案例,采取教师讲授引导并结合学生探究式、体验式等授课 模式尚可取得良好效果 三、教学设计 通过两个建模案例介绍,引导学生体验从实际问题中提取数学结构的过程,探究 “学着用”数学与“学习”数学有根本差异,对数学模型及数学建模有初步概要的了解,为 后续引进数学模型概念做好感性铺垫 帮助学生了解到建模过程的以下特征: 1)不明确性,问题没有设定具体需解决的问题和求解的条件: 2)不唯一性,模型不唯一、方法不唯一,没有唯一正确解答答案: 3)主观性,描述实际研究对象的规律性带有较强的主观性: 4)试错性,是原创性的工作过程,需要不断探索、试错并纠错 案例1:人口增长模型尝试建立数学模型预测人口数量变化, 1.问题前期分析 问题1影响1时刻某地区的人口总数变化的最显著因素应包括哪些? 问题2你们准备考虑哪些因素?将考虑哪些变量? 问题3用什么变量描述人口变化情况?人口密度还是人口总数? 引导学生尽可能多的列出影响因素基础上,讨论确定仅考虑出生和死亡对人口变化的 影响,并用人口总数描述地区人口变化 2.建立数学模型 问题4在时间段北,什△]内出生和死亡所致人口数量变化与哪些变量有关? 讨论结论出生率和死亡率、人口基数、时间间隔△1的长短 1)固定时间长度为单位1的条件下,建立差分方程人口模型
这是一个应用数学家的信仰.”—— 应用数学大师林家翘 第二章 数学的应用 一、教学内容及要求(6 学时) 了解数学的抽象性和逻辑性; 了解数学研究对象的多样性与内部的统一性;了解数学应 用的广泛性与描述的精确性.了解应用数学过程的五个阶段性工作: 识别和剖析问题、提取数 学结构、描述数学问题、科学计算、解释评判结论. 二、教学重点、难点及解决办法 学习数学理论知识与应用数学有极大差异, 需转变学生的学习理念和学习方法.建模过 程的五个阶段性工作是应用数学的重要环节, 且涉及到对数学的全面认知, 仅依靠老师抽象 讲授学生很难理解, 选择恰当的案例, 采取教师讲授引导并结合学生探究式、体验式等授课 模式尚可取得良好效果. 三、教学设计 通过两个建模案例介绍, 引导学生体验从实际问题中提取数学结构的过程, 探究 “学着用”数学与 “学习”数学有根本差异, 对数学模型及数学建模有初步概要的了解, 为 后续引进数学模型概念做好感性铺垫. 帮助学生了解到建模过程的以下特征: 1)不明确性, 问题没有设定具体需解决的问题和求解的条件; 2)不唯一性, 模型不唯一、方法不唯一, 没有唯一正确解答答案; 3)主观性, 描述实际研究对象的规律性带有较强的主观性; 4)试错性, 是原创性的工作过程, 需要不断探索、试错并纠错. 案例 1:人口增长模型 尝试建立数学模型预测人口数量变化. 1. 问题前期分析 问题 1 影响 t 时刻某地区的人口总数变化的最显著因素应包括哪些? 问题 2 你们准备考虑哪些因素?将考虑哪些变量? 问题 3 用什么变量描述人口变化情况?人口密度还是人口总数? 引导学生尽可能多的列出影响因素基础上, 讨论确定仅考虑出生和死亡对人口变化的 影响, 并用人口总数描述地区人口变化. 2.建立数学模型 问题 4 在时间段[t, t+ t] 内出生和死亡所致人口数量变化与哪些变量有关? 讨论结论 出生率和死亡率、人口基数、时间间隔t 的长短. 1)固定时间长度为单位 1 的条件下, 建立差分方程人口模型

2)在N趋于等的情况下,离散问愿连续化建立微分方程大晋=b-d,得到Mathus人 口模型Nt)=Noe",t≥0 3.数学模型分析 问题5以上两个人口模型哪个更“好”? 问题6怎样评判模型的优与劣? 引导学生分析两个模型,使学生理解不同的假设建立模型不同,有不同的适用范围,并 且察觉Malthus模型的不合理之处,讨论得出假设“净相对增长率r是常数”不合乎实际背 景,并提出猜想“人口净增长率与人口数量有关” 4.数学棋型改进 问题7怎样描述增长率和人口数的关系? 试错:将“人口净增长率”视为人口量的函数),不能求出人口函数: 主观设置函数:将净增长率r看成人口数N的线性函数r(W)=a+cN,建立微分方程,求 解得Logistic人口模型 NoKert K t≥0 K+(e”-)1+(-1en 5.数学模型分析与检验 对此模型做数学分析和实际检验,研讨得结论:Malthus模型适合描述初期高速变化的人 口数量,Logistic人口模型则适合描述较长时间内,增长速度出现拐点的人口变化情况.帮助 学生认识到数学模型没有“对错”,只有适用于否 通过关于分析人口模型的不断演化和发展,在区分模型不同的同时,体会研究成果的局 限性,培训学生实事求是的科学精神和辩证唯物主义意识观 案例2:桌子能放稳吗? 1.课堂探究环节 此案例以问题牵引讨论为主,促使学生参与并体验如何将一个似乎与数学无关的问题 抽象为典型数学问题的全过程,竭力开拓学生的思维 实际问题:小李的方形书桌在固定位置怎么都放不平稳,有什么办法可以将桌子放稳 吗? 问题1你考虑怎样置放桌子? 如,将桌子固定在一个小范围不做移动, 只让其绕中心转动 随机置放 沿水平方向平移抬动(抬动)
2)在t 趋于零的情况下, 离散问题连续化建立微分方程 b d dt dN N 1 , 得到 Malthus 人 口模型 N(t) = N0ert, t ≥0. 3.数学模型分析 问题 5 以上两个人口模型哪个更“好”? 问题 6 怎样评判模型的优与劣? 引导学生分析两个模型, 使学生理解不同的假设建立模型不同, 有不同的适用范围, 并 且察觉 Malthus 模型的不合理之处, 讨论得出假设“净相对增长率 r 是常数”不合乎实际背 景, 并提出猜想“人口净增长率与人口数量有关”. 4.数学模型改进 问题 7 怎样描述增长率和人口数的关系? 试错:将“人口净增长率”视为人口量的函数 r(N), 不能求出人口函数; 主观设置函数:将净增长率 r 看成人口数 N 的线性函数 r(N)=a+ c N, 建立微分方程, 求 解得 Logistic 人口模型 , 0 ( 1) 1 ( 1) ( ) 0 0 0 t rt e N K K rt K N e rt N Ke N t 5.数学模型分析与检验 对此模型做数学分析和实际检验, 研讨得结论:Malthus 模型适合描述初期高速变化的人 口数量, Logistic 人口模型则适合描述较长时间内, 增长速度出现拐点的人口变化情况.帮助 学生认识到数学模型没有“对错”, 只有适用于否. 通过关于分析人口模型的不断演化和发展, 在区分模型不同的同时, 体会研究成果的局 限性, 培训学生实事求是的科学精神和辩证唯物主义意识观. 案例 2:桌子能放稳吗? 1.课堂探究环节 此案例以问题牵引讨论为主, 促使学生参与并体验如何将一个似乎与数学无关的问题 抽象为典型数学问题的全过程, 竭力开拓学生的思维. 实际问题:小李的方形书桌在固定位置怎么都放不平稳, 有什么办法可以将桌子放稳 吗? 问题 1 你考虑怎样置放桌子? 如, 将桌子固定在一个小范围不做移动, 只让其绕中心转动. 随机置放 沿水平方向平移抬动(抬动)