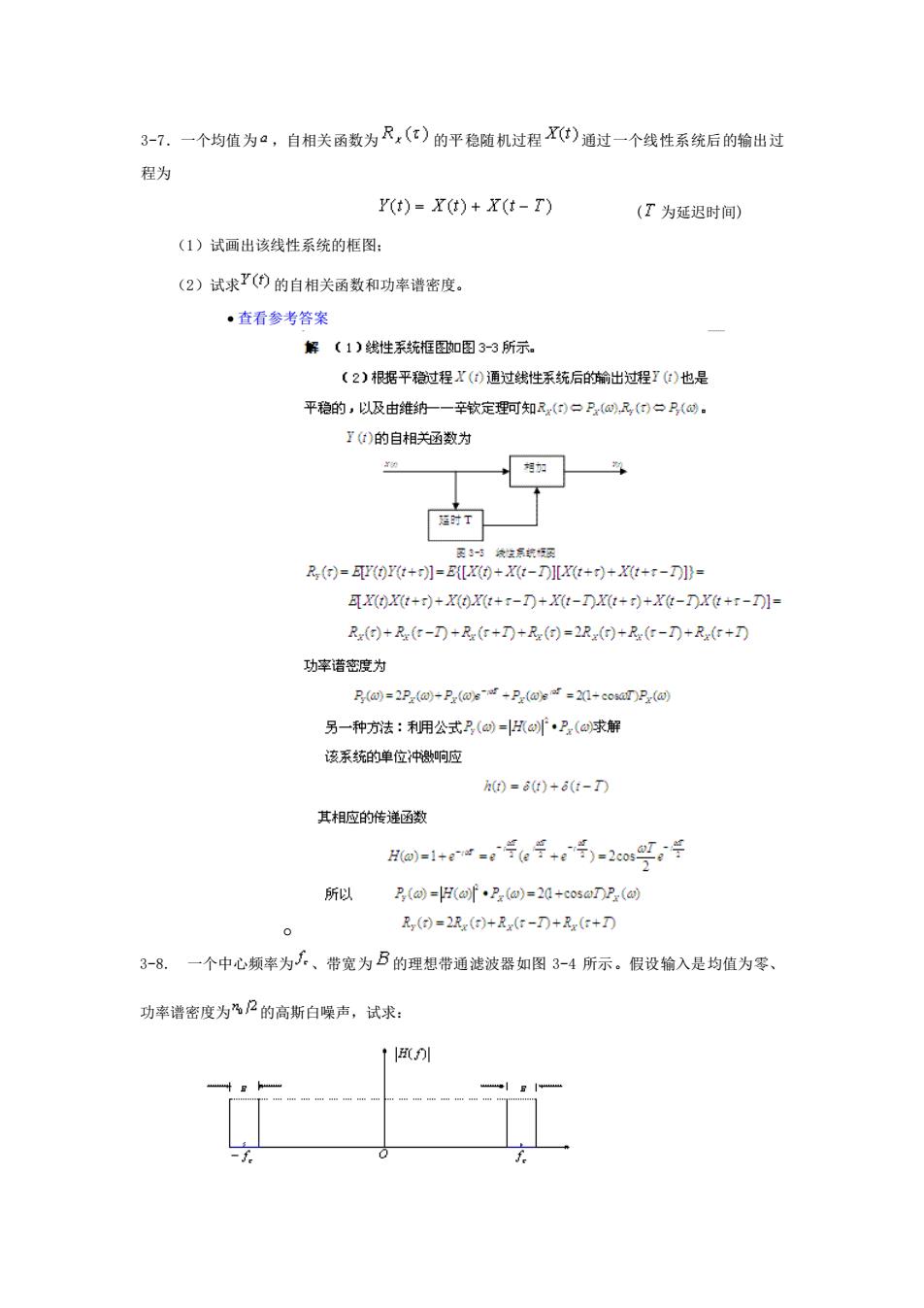
3-7.一个均值为,自相关函数为R,(©)的平稳随机过程0)通过一个找性系统后的输出过 程为 r()=X)+X(t-T) (T为延迟时间) (1)试画出该线性系统的框图: (2)试求”(⑨的自相关函数和功率谱密度。 ·查看参考答案 解(1)线性系统框图如图33所示, 〔2)根据平稳过程X()通过线性系统后的输出过煜了(:)也是 平稳的,以及由维纳一辛软定程可知,@们一. :)的自相关通数为 T】 可0X++0+r-刀+xt-Dxt+)+xt-刀xe+r-D1= R+Rr-D+Rr+D+R句=2Rr+Rr-刀+R+D 功宰谐密度为 另一种方法:利用公式2(=2(求解 该系统的单位冲激p应 h()■+6(t-T 其相应的传函数 io-1+g-gfe年+ef)-2号 所似 2,(a=Haf2(@)=2+csn2(@ R()=2E,()+2,(:-TD+R(:+D 3-8.一个中心频率为、带宽为B的理想带通滤波器如图3-4所示。假设输入是均值为零、 功率谱密度为%2的高斯白噪声,试求:
3-7.一个均值为 ,自相关函数为 的平稳随机过程 通过一个线性系统后的输出过 程为 ( 为延迟时间) (1)试画出该线性系统的框图; (2)试求 的自相关函数和功率谱密度。 • 查看参考答案 o 3-8. 一个中心频率为 、带宽为 的理想带通滤波器如图 3-4 所示。假设输入是均值为零、 功率谱密度为 的高斯白噪声,试求:

图3-4 (1)滤波器输出噪声的自相关函数: (2)滤波器输出噪声的平均功率 (3)输出噪声的一维概率密度函数。 ·查看参考答案 解: (1)已知高斯白噪声的功率诺密度门-号,所以滤波器输出噪 声的功宰密度 -生归Jf- 号1-号ns以是 /0 其地 根据只)一兄(),输出晚声%e的自相关函数 %58a(5)c2对. 〔2)G的平均的功率 V。-凡(的-既日 N,-A-u,5 〔3)高斯听过程通过线性系统后的输出仍为高过程,且有 可院g】=[既]·H0)=0 。产-%-R⑨-式(列-%5 因此,出噪声的一维宰密度函数 0 3-9。一个C低通滤波器如图3-5所示,假设输入是均值为零、功率谱密度为%P的高斯白噪 声,试求: (1)输出噪声的功率谱密度和自相关函数 (2)输出噪声的一维概率密度函数。 。 R 图3-5 ·查看参考答案
图 3-4 (1)滤波器输出噪声的自相关函数; (2)滤波器输出噪声的平均功率; (3)输出噪声的一维概率密度函数。 • 查看参考答案 o 3-9. 一个 RC 低通滤波器如图 3-5 所示,假设输入是均值为零、功率谱密度为 的高斯白噪 声,试求: (1)输出噪声的功率谱密度和自相关函数; (2)输出噪声的一维概率密度函数。 图 3-5 • 查看参考答案

解(1)贮低源滤波器的传涵数 H() 翰出噪声儿(的功率道密度为 根据R,)台B(),并利用 州 可得%:的自相关函数 〔2)根随机过程通过线性系统的理论,可得输出噪声%的 均值 Eu,(明-E,(·HO)-0 和方差 。%-无-无 因为高斯过提通过线系统后的出仍为高斯过煜,所似出声 的一维宰密度函数 f(x)■ 评注:高斯过程通过线性系统后的输出仍为高斯过程,但数宇特 。可能变化。 3-10.一个LR低通滤波器如图3-6所示,假设输入是均值为零、功率谱密度为%2的高斯断白 噪声,试求: (1)输出噪声的自相关函数: (2)输出噪声的方差。 R 图3-6 ·查看参考答案
o 3-10. 一个 LR 低通滤波器如图 3-6 所示,假设输入是均值为零、功率谱密度为 的高斯白 噪声,试求: (1)输出噪声的自相关函数; (2)输出噪声的方差。 图 3-6 • 查看参考答案

解(1)低通滤波器的传输函数 出噪声的功率话变度力会入 根据元份=®,并利用入 州白+ 可得输出噪声的自相关函数 &赞别 (2)输出噪声的方差。-@)-无倒)一是 3-11.设有一个随机二进制矩形脉冲波形,它的每个脉冲的持续时间为T。,脉冲幅度取±1的 概奉相等。现假设任一间隔。内波形取值与任何别的间隔内取值统计无关,且具有宽平稳性, 试证: 1-x 1)自相关函数R:(c)-0 H> (2)功率谱密度(回=1,,P 3-12.图3-7为单个输入、两个输出的线性滤波器,若输入过程7心是平稳的,求⑨与)的 h.() 互功率密度的表达式。 图3-7 。查看参考答案
o 3-11.设有一个随机二进制矩形脉冲波形,它的每个脉冲的持续时间为 ,脉冲幅度取 的 概率相等。现假设任一间隔 内波形取值与任何别的间隔内取值统计无关,且具有宽平稳性, 试证: (1)自相关函数 = (2)功率谱密度 3-12. 图 3-7 为单个输入、两个输出的线性滤波器,若输入过程 是平稳的,求 与 的 互功率密度的表达式。 图 3-7 • 查看参考答案

解由题意可知,这是一个等发送的双极性拒形肱冲序列,可参 考G通信原理(第6版)的第6章138页式(6.1-26)和140页【例 62】,不难证明 P(a)-IlSalT,) 根据维钠一一软定理:?(一A,(),利用S函数一门函数, 两个函数相乘一两个门还数卷积,可以证明自相关函数为一三角 波,即 。证明过程省。 3-13.设平稳过程X()的功率谱密度为P(@),其自相关函数为尺,()。试求功率谱密度为 (0+a)+P(0-a,》所对应的过程的自相关函数(其中,⑧为正常数)· 3-14.X()是功率谱密度为P.()的平稳随机过程,该过程通过图3-8所示的系统。 图3-8 (1)输出过程Y(⑤是否平稳? (2)求P()的功率瑞密度。 。查看参考答案 解〔1)因为线性系统的端入:(0是平稳过程,所以其出过程 了G)也是平稳的. 〔2)该系统的传待函数 -+8j8-28g:号, )的功率诺密度 0 -日af,(-2证- 3=15设X0是平稳随机过程,其自相关函数在~1.D上为R同-0-中,是网期为2的 周期性函数。试求《0的功率端密度P(回,并用图形表示。 ·查看参考答案
o 3-13.设平稳过程 的功率谱密度为 ,其自相关函数为 。试求功率谱密度为 所对应的过程的自相关函数(其中, 为正常数)。 3-14. 是功率谱密度为 的平稳随机过程,该过程通过图 3-8 所示的系统。 图 3-8 (1)输出过程 是否平稳? (2)求 的功率谱密度。 • 查看参考答案 o 3-15. 设 是平稳随机过程,其自相关函数在(-1,1)上为 ,是周期为 2 的 周期性函数。试求 的功率谱密度 ,并用图形表示。 • 查看参考答案