
0122229现代数字通信与编码理论 November 10.2011 XDU,Fall 2011 Lecture Notes 4.8 Low-Density Parity-Check Codes Low-density parity-check (LDPC)codes are a class of linear block codes with near capacity performance, which was invented by Gallager in the in his Ph.D.thesis and were rediscovered in late 1990's.They are constructed using sparse bipartite graph(hence the name low-density),and can be decoded iteratively based on sum-product algorithm. LDPC codes have proved capable of approaching the Shannon limit more closely than any other class of codes. Ever since thei rediscovery,desig construction,decoding.efficient encoding performance analysis,and applications of LDPC codes in digital communication and storage systems have become focal points of research. Note:Some of material presented in this section is based on Prof.Shu Lin's lecture notes and S.J.Johnson's notes. 4.8.1 Definitions and Basic Concepts Although LDPC codes can be generalized to nonbinary alphabets,we will consider only binary codes in this section for the sake of simplicity. A binary LDPC code is a special class of(n)linear block codes whose parity-check matrix H=[h]contains mostly 0's and relatively few I's;i.e.,H is sparse.This sparsity renders low complexity decoding and leads to simple implementations.In particular,an (n,d de)regular LDPC code is a binary linear block code of length n,whose parity-check matrix H contains exactly d I's in each column and d I's in each row.This means that every coded bit participates in exactly ns and that every such check equation involves exactlycoded bits.A formal definition is as follows Definition 4.8.1:A binary regular LDPC code is defined as the null space of a sparse parity-check matrix H over GF(2)with the following structural properties: 1)Each row has constant weightd 2)Each has constant weight 3)No two rows(or two columns)have more than one 1-component in common;and 4)Both de and d,are small compared to code length and the number of rows in H. The H with these properties will be said to be(dde)-regular,and the code generated by such H will be called a(d,de)-regular LDPC code. to as the row and column (RC)const The RC-constraint on the rows and columns of H ensures that nodor fewer columns of H can be added to zero.As a result,the minimum distance of the LDPC code given by the null space of H is at least d+1. Because both de and d,are small compared to code length and the number of rows in the matrix,H therefore has a low density of I's.In literature,the density r of the parity-check
1 0122229 现代数字通信与编码理论 November 10, 2011 XDU, Fall 2011 Lecture Notes 4.8 Low-Density Parity-Check Codes Low-density parity-check (LDPC) codes are a class of linear block codes with near capacity performance, which was invented by Gallager in the early 1960’s in his Ph.D. thesis and were rediscovered in late 1990’s. They are constructed using sparse bipartite graph (hence the name low-density), and can be decoded iteratively based on sum-product algorithm. LDPC codes have proved capable of approaching the Shannon limit more closely than any other class of codes. Ever since their rediscovery, design, construction, decoding, efficient encoding, performance analysis, and applications of LDPC codes in digital communication and storage systems have become focal points of research. Note: Some of material presented in this section is based on Prof. Shu Lin’s lecture notes and S. J. Johnson’s notes. 4.8.1 Definitions and Basic Concepts Although LDPC codes can be generalized to nonbinary alphabets, we will consider only binary codes in this section for the sake of simplicity. A binary LDPC code is a special class of (n, k) linear block codes whose parity-check matrix [ ]ij H = h contains mostly 0’s and relatively few 1’s; i.e., H is sparse. This sparsity renders low complexity decoding and leads to simple implementations. In particular, an (n, dv, dc) regular LDPC code is a binary linear block code of length n, whose parity-check matrix H contains exactly dv 1’s in each column and dc 1’s in each row. This means that every coded bit participates in exactly dv parity-check equations and that every such check equation involves exactly dc coded bits. A formal definition is as follows. Definition 4.8.1: A binary regular LDPC code is defined as the null space of a sparse parity-check matrix H over GF(2) with the following structural properties: 1) Each row has constant weight dc ; 2) Each column has constant weight dv ; 3) No two rows (or two columns) have more than one 1-component in common; and 4) Both dc and dv are small compared to code length and the number of rows in H. The H with these properties will be said to be (dv, dc)-regular, and the code generated by such H will be called a (dv, dc)-regular LDPC code. Property 3) is referred to as the row and column (RC) constraint. The RC-constraint on the rows and columns of H ensures that no dv or fewer columns of H can be added to zero. As a result, the minimum distance of the LDPC code given by the null space of H is at least dv+1. Because both dc and dv are small compared to code length and the number of rows in the matrix, H therefore has a low density of 1’s. In literature, the density r of the parity-check

matrix H is defined as the ratio of the total number of 1's in H to the total number of entries in H.Let m be the number of rows in H(i.e suppose that H is an mn matrix).We readily see that n m Since d and de are related by d.m=dn,the nominal code rate R can be computed by =1-4 (4.1) n d The actual rate of the code specified by H may be higher since these m rows of H(m check equations)might not all be independent. Definition48.2 If H is sparse,but the number of I's in each column or in each row is not constant,the resulting code is called an irregular LDPC code. In general,irregular LDPC codes have a better performance than regular LDPC codes. Recall that a squ rix is called a circulant matrix(simply a circulant)if each row is a cyclic-shift (one place to the right or the left)of the row above it and the first row is the cyclic-shift of the last row. Definition 483:An ldPC code is said to be cvclic if its parity-check matrix consists of a colum n of circulants.An LDPC code is said to be quasi-cyclic (QC)if its parity -check matrix consists of an array of circulants The encoding of a cyclic or a QC-LDPC code can be implemented with simple shift-register(s). Example 4.8.1:Consider the matrix given below: 「1011000 0101100 0110 H 1011 (4.2) 000101 1100010 0110001 This matrix has both column and r weights 3.We can easily check that rows (or two columns)have more than one 1-componen in common.Therefore the matri satisfies the RC-constraint.It is a (3.3)-regular matrix.It is also seen that H is a circulant The null space of H gives a(7,3)cyclic-LDPC code with minimum distanced=4
2 matrix H is defined as the ratio of the total number of 1’s in H to the total number of entries in H. Let m be the number of rows in H (i.e., suppose that H is an m×n matrix). We readily see that c v d d r n m = = Since dv and dc are related by c v dm dn = , the nominal code rate Rc can be computed by 1 v c c n m d R n d − = = − (4.1) The actual rate of the code specified by H may be higher since these m rows of H (m check equations) might not all be independent. Definition 4.8.2: If H is sparse, but the number of 1’s in each column or in each row is not constant, the resulting code is called an irregular LDPC code. In general, irregular LDPC codes have a better performance than regular LDPC codes. Recall that a square matrix is called a circulant matrix (simply a circulant) if each row is a cyclic-shift (one place to the right or the left) of the row above it and the first row is the cyclic-shift of the last row. Definition 4.8.3: An LDPC code is said to be cyclic if its parity-check matrix consists of a column of circulants. An LDPC code is said to be quasi-cyclic (QC) if its parity-check matrix consists of an array of circulants. The encoding of a cyclic or a QC-LDPC code can be implemented with simple shift-register(s). Example 4.8.1: Consider the matrix given below: 1011000 0101100 0010110 0001011 1000101 1100010 0110001 ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ H (4.2) This matrix has both column and row weights 3. We can easily check that there are no two rows (or two columns) have more than one 1-component in common. Therefore the matrix satisfies the RC-constraint. It is a (3, 3)-regular matrix. It is also seen that H is a circulant. The null space of H gives a (7, 3) cyclic-LDPC code with minimum distance min d = 4

have seen in ection 4.6 that a linear block code can also be represented by aTanne graph (or factor graph,normal graph),which actually provides a graphical representation of the parity-check matrix H.The n variable nodes represent the columns of H,and the m constraint(check)nodes represent the rows of H.There exists an edge between the check node i and the variable node j if and only if the entryh=1.Thus,for an (n,dd)regular LDPC code,there are nd,=md edges in the graph,d,edges incident to each variable node and d edges incident to each check node.As an example,Fig.4.8.1 shows the Tanner graph for a (10,5)linear block code withd=3,de=6,and the parity-check matrix [11110110 00] 0011111100 H=0101010111 (4.3) 1010100111 1100101011 Let x denote a codeword.From xH=0,we can see that for each check node,the sum of all adjacent variable nodes is equal to zero.That is,check nodes are zero-sum constraints. C3 + S1 C4 S2 + S3 + S4 S5 cg○ Figure 4.8.1 Tanner graph for a(10,5)linear block code.Note that each variable node is of degree 3 and each check node is of degree 6. The parity-check matrix H of a code is actually the incidence matrix of its Tanner graph 3
3 4.8.1.2 Graphical Representation of LDPC codes We have seen in Section 4.6 that a linear block code can also be represented by a Tanner graph (or factor graph, normal graph), which actually provides a graphical representation of the parity-check matrix H. The n variable nodes represent the columns of H, and the m constraint (check) nodes represent the rows of H. There exists an edge between the check node i and the variable node j if and only if the entry hij = 1. Thus, for an (n, dv, dc) regular LDPC code, there are v c nd md = edges in the graph, dv edges incident to each variable node and dc edges incident to each check node. As an example, Fig. 4.8.1 shows the Tanner graph for a (10, 5) linear block code with dv = 3, dc = 6, and the parity-check matrix 1111011000 0011111100 0101010111 1010100111 1100101011 ⎡ ⎤ ⎢ ⎥ = ⎣ ⎦ H (4.3) Let x denote a codeword. From T xH 0 = , we can see that for each check node, the sum of all adjacent variable nodes is equal to zero. That is, check nodes are zero-sum constraints. Figure 4.8.1 Tanner graph for a (10, 5) linear block code. Note that each variable node is of degree 3 and each check node is of degree 6. The parity-check matrix H of a code is actually the incidence matrix of its Tanner graph

Therefore,we also refer to the Tanner graph of a code as the Tanner graph of its parity-check matrix H. [Cycle and Girth:A cycle of length I in a Tanner graph is a path comprised of edges which closes back on itself.The minimum cycle length of the graph is called the girth of the graph. Clearly,the shortest possible cycle in a bipartite graph is a length-4 cycle,which manifest thems elves in the H matrix as four I's that lie an th corners of a submatrix of H. Figure 4.8.2 As stated in Section 4.7,the cycles,particularly short cycles will degrade the perfor rmance of the iterative decoding algo e for LDPC cod The cycles that affec the decoding performance the most are the cycles of length 4.Therefore.in constructing LDPC codes.cycles of length 4 must be avoided. If the parity-check matrix H of a binary linear block code satisfies the RC-constraint,then wocoddcan e checked simultanously by two parity-check sums.As a result the girth of at least 6.Since we Fan LDPC cod regularor,satisfies the RC-constraint the Tanner graph of an LDPC code has a girth of at least 6. Example 4.8.2:The Tanner graph of the (7,3.3)LDPC code given in Example 1 is shown in Fig.4.8.3
4 Therefore, we also refer to the Tanner graph of a code as the Tanner graph of its parity-check matrix H. Definition 4.8.4 [Cycle and Girth]: A cycle of length l in a Tanner graph is a path comprised of l edges which closes back on itself. The minimum cycle length of the graph is called the girth of the graph. Clearly, the shortest possible cycle in a bipartite graph is a length-4 cycle, which manifest themselves in the H matrix as four 1’s that lie an the corners of a submatrix of H. . 1 1 . 1 1 . ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ H Figure 4.8.2 As stated in Section 4.7, the cycles, particularly short cycles will degrade the performance of the iterative decoding algorithm used for LDPC codes. The cycles that affect the decoding performance the most are the cycles of length 4. Therefore, in constructing LDPC codes, cycles of length 4 must be avoided. If the parity-check matrix H of a binary linear block code satisfies the RC-constraint, then no two coded bits can be checked simultaneously by two parity-check sums. As a result, the Tanner graph of the code is free of cycles of length 4 and has a girth of at least 6. Since we require that the matrix H of an LDPC code, regular or irregular, satisfies the RC-constraint, the Tanner graph of an LDPC code has a girth of at least 6. Example 4.8.2: The Tanner graph of the (7, 3, 3) LDPC code given in Example 1 is shown in Fig. 4.8.3
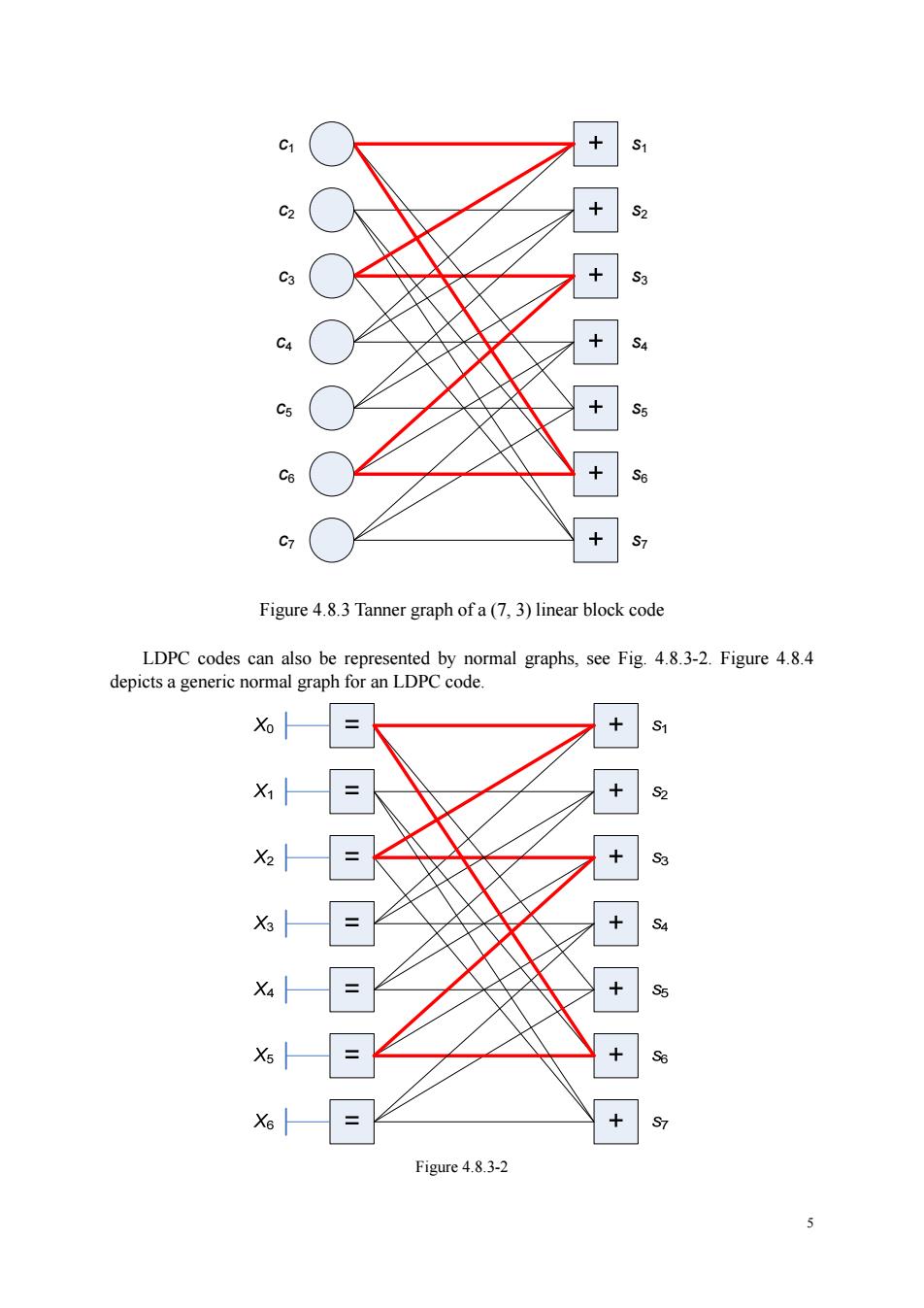
+s + Se +s7 Figure 4.8.3 Tanner graph of a(7,3)linear block code LDPC be repre resented by normal graphs,see Fig.4.8.3-2.Figure 4.8.4 depicts a generic normal graph for an LDPC code Xo X + = Figure4.8.3-2
5 c1 c2 c3 c4 c5 c6 c7 s1 s2 s3 s4 s5 s6 s7 Figure 4.8.3 Tanner graph of a (7, 3) linear block code LDPC codes can also be represented by normal graphs, see Fig. 4.8.3-2. Figure 4.8.4 depicts a generic normal graph for an LDPC code. Figure 4.8.3-2