
1、二元阵与方向图乘积定理 已知天线阵的排列方法:即天线个数、间距、各天 线上电流的振幅和相位,分析它的方向性,这种方法叫 做天线阵的分析理论。 另一种是给出所需方向图,反过来求形成该方向图 天线阵的组成和天线个数、间距、线元电流的振幅和相 位分布等,这种理论称为天线阵的综合理论。 我们分析用第一种方法,而实际应用则采用第二种 方法。 方向图乘积定理:天线阵总的方向图等于天线单独 存在时的方向图(方向函数)乘以排列的阵因子(阵函 数)方向图。 STE A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 1 1、二元阵与方向图乘积定理 已知天线阵的排列方法:即天线个数、间距、各天 线上电流的振幅和相位,分析它的方向性,这种方法叫 做天线阵的分析理论。 另一种是给出所需方向图,反过来求形成该方向图 天线阵的组成和天线个数、间距、线元电流的振幅和相 位分布等,这种理论称为天线阵的综合理论。 我们分析用第一种方法,而实际应用则采用第二种 方法。 方向图乘积定理:天线阵总的方向图等于天线单独 存在时的方向图(方向函数)乘以排列的阵因子(阵函 数)方向图

设由空间取向一致的两个结构尺寸相同的天线构成一 个二元阵,如图所示。两元的距离为d,电流分别为L1,和 L2,且有I2=ml1e,这里m为两电流的振幅比,飞为两电流 的相位差。由于观察点M距天线很远,故可认为阵元“1” 和“2”至M点的两射线相互平行,则 r=r-dcose 式中,为射线与阵轴之间的夹角。 由于两天线元符合相似元的条件, 因此其归一化方向函数F(0=F(=F(0。 则两天线元在M点产生的场强分别为 E1=E1mF(0) E2 =mEF()e(+kdeoso) STE A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 2 设由空间取向一致的两个结构尺寸相同的天线构成一 个二元阵,如图所示。两元的距离为 d ,电流分别为I1,和 I2,且有 I2= mI1 e j,这里m为两电流的振幅比,为两电流 的相位差。由于观察点 M 距天线很远,故可认为阵元“ 1 ” 和“ 2 ”至 M 点的两射线相互平行,则 cos 2 1 r r d 式中, 为射线与阵轴之间的夹角。 由于两天线元符合相似元的条件, 因此其归一化方向函数 Fl ()=F2 ()=F()。 则两天线元在 M 点产生的场强分别为 0 ) ) ( cos ) 1 1 2 1 m j kd m E E F E mE F e

M点的合成场为 E=E+E2=EF(e)(1+me) 其中 y=s+kd cos 设 fn(0)=1+me 则 E=EmF(O)fa(O)=Emf阵列(O) 其中f阵列(0)=F(0)f(O) 上式即为方向图乘积定理,即由相似元所构成的天线阵列的 方向性函数等于各阵元单独存在时的方向性函数F()(称 为元因子)和阵方向函数f(0)(称为阵因子)的乘积。 STE_A.J.YUE 西安电子科技大学通信工程学院 3
STE_A.J.YUE 西安电子科技大学通信工程学院 3 M 点的合成场为 其中 设 则 其中 上式即为方向图乘积定理,即由相似元所构成的天线阵列的 方向性函数等于各阵元单独存在时的方向性函数 F( )(称 为元因子)和阵方向函数f a ( )(称为阵因子)的乘积。 )( ) 1 2 1 1 j E E E E F me m kd cos ( ) 1 j a f me ) ( ) ( ) E E F f E f 1 1 m a m 阵列 阵列 ( ) ( ) = ) a f F f

等幅二元阵(m=1)的阵因子为: Ls(o-+meM-+e 2 下面讨论几种等幅二元阵(m=1)的阵因子。 2、等幅二元阵的几种典型情况: STE A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 等幅二元阵(m = 1)的阵因子为: ( ) cos cos cos = 1 = 1 =2 2 2 2 j j a f me e kd 下面讨论几种等幅二元阵(m = 1)的阵因子。 2、等幅二元阵的几种典型情况: 4
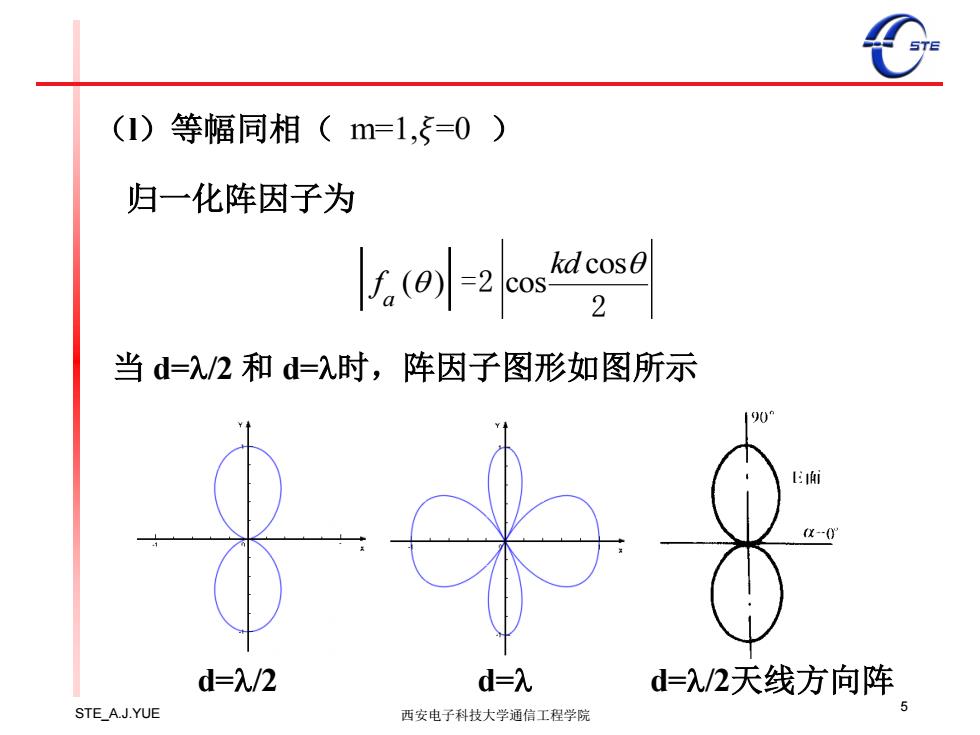
(1)等幅同相(m=1,=0) 归一化阵因子为 outose 当d=乳/2和d=入时,阵因子图形如图所示 0 面 (x-0 d=λ/2 d=λ d=λ/2天线方向阵 STE_A.J.YUE 西安电子科技大学通信工程学院
STE_A.J.YUE 西安电子科技大学通信工程学院 5 (l)等幅同相( ) 当 d=l/2 和 d=l时,阵因子图形如图所示 归一化阵因子为 cos ( ) cos = 2 2 a kd f d=l/2 d=l d=l/2天线方向阵