
§2.5二端口网络及其网络参量 S矩阵与Z矩阵7矩阵的变换 由0=S00=0,+0i=0,-0,0=元i=z 可得: S=(Z-1)(2+1)=(1-T)(1+)1 7=(1+S)(1-S) T=(1-S)(1+S)1 双端口网络S参数讨论 对于常用的双端口微波网络,S参数方程为: 0n1=S01+S02 02=S201+S02
S Z Y 矩阵与 矩阵 矩阵的变换 §2.5 二端口网络及其网络参量 U SU r i U U U i r i r 由 I U U U ZI I YZ 可得: 1 1 S ( ( Z-1)(Z+1) 1-Y)(1+Y) 1 1 ( ( Z 1+S)(1-S) Y 1-S)(1+S) 双端口网络S参数讨论 对于常用的双端口微波网络,S参数方程为: 1 11 1 12 2 2 21 1 22 2 r i i r i i U S U S U U S U S U

§2.5二端口网络及其网络参量 1、无耗互易性: 由无耗网络的一元性可知: Su+Sa=1 S1S12+S21S22=0 S22+lS22-, S2S1+S2S21=0 若网络互易,则有:S=S2 ISu=S22 可见,对于无耗互易网络,即使不对称,也有 ISu=IS2l
由无耗网络的一元性可知: 1、无耗互易性: 2 2 11 21 11 12 21 22 2 2 22 12 12 11 22 21 + 1 + =0 + 1 + =0 S S S S S S S S S S S S , , 可见,对于无耗互易网络,即使不对称,也有 若网络互易,则有: S S 11 22 = S S 11 22 = S S 11 22 = §2.5 二端口网络及其网络参量
§2.5二端口网络及其网络参量 2、S矩阵和A矩阵关系: S矩阵有明确的物理含义,但不便于分析级联双端口网络, 因此分析级联网络特性时,总是先求出总的级联网络A参数, 再转化为$矩阵的方法,所以要熟悉S矩阵和A矩阵的关系。 41+412-021-02 2detA S= 411+412+a21+a22 a11+a12+a21+a22 2 -411+412-421+a22 a11+a12+a21+a2 a11+a12+a21+a22 A a a12 21 d22
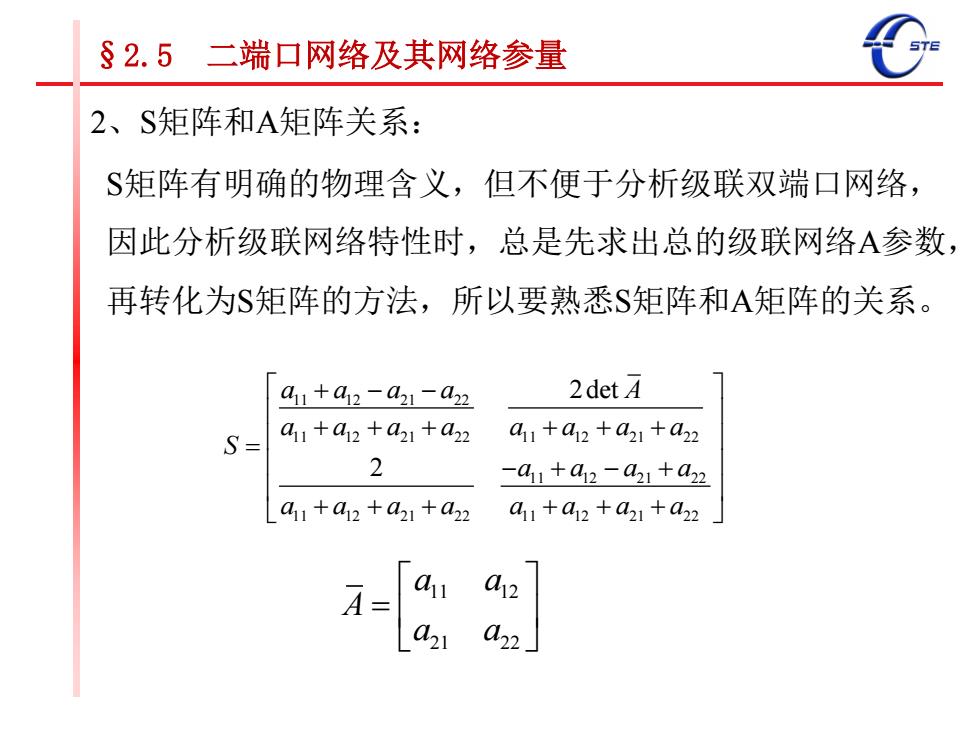
2、S矩阵和A矩阵关系: S矩阵有明确的物理含义,但不便于分析级联双端口网络, 因此分析级联网络特性时,总是先求出总的级联网络A参数, 再转化为S矩阵的方法,所以要熟悉S矩阵和A矩阵的关系。 11 12 21 22 11 12 21 22 11 12 21 22 11 12 21 22 11 12 21 22 11 12 21 22 2det 2 a a a a A a a a a a a a a S a a a a a a a a a a a a 11 12 21 22 a a A a a §2.5 二端口网络及其网络参量

§2.5二端口网络及其网络参量 3、输入端反射系数与负载关系 负载端反射系数 02 输入端反射系数 m 0=S+ S2S2TL S22L 4、S参数测量 微波网络理论实际意义在于网络参数可以直接用实验的 方法测量,根据反射系数和$参数关系,可以通过测量反射 系数,计算S参数
3、输入端反射系数与负载关系 负载端反射系数 2 2 i L r U U 输入端反射系数 1 12 21 11 1 22 r L in i L U S S S U S 4、S参数测量 微波网络理论实际意义在于网络参数可以直接用实验的 方法测量,根据反射系数和S参数关系,可以通过测量反射 系数,计算S参数。 §2.5 二端口网络及其网络参量

§2.5二端口网络及其网络参量 阻抗法测网络S参数 对互易两端口网络,三次独立测量,确定网络$参数: T2负面负载 T2参考面 T1参考面 匹配 「,=0 Tw=Su 短路 T,=-1 Tis=Su+ S足 +1+S2 开路 「z=1 To=Su+1-Sa 解方程可得: S,=「iM 2Tw-Ts-「o Tis-Tio 2(Ti-Tis)(TiM-Tio) 12 Tis-Tio
阻抗法测网络S参数 对互易两端口网络,三次独立测量,确定网络S参数: 0 L 12 11 1 1 1 1 22 1 1 2 1 1 1 1 1 1 2 2( )( ) M M S O S O M S M O S O S S S T2参考面 1 11 M S T2负面负载 T1参考面 匹配 短路 开路 1 L 1 L 2 12 1 11 22 1 S S S S 2 12 1 11 22 1 O S S S 解方程可得: §2.5 二端口网络及其网络参量