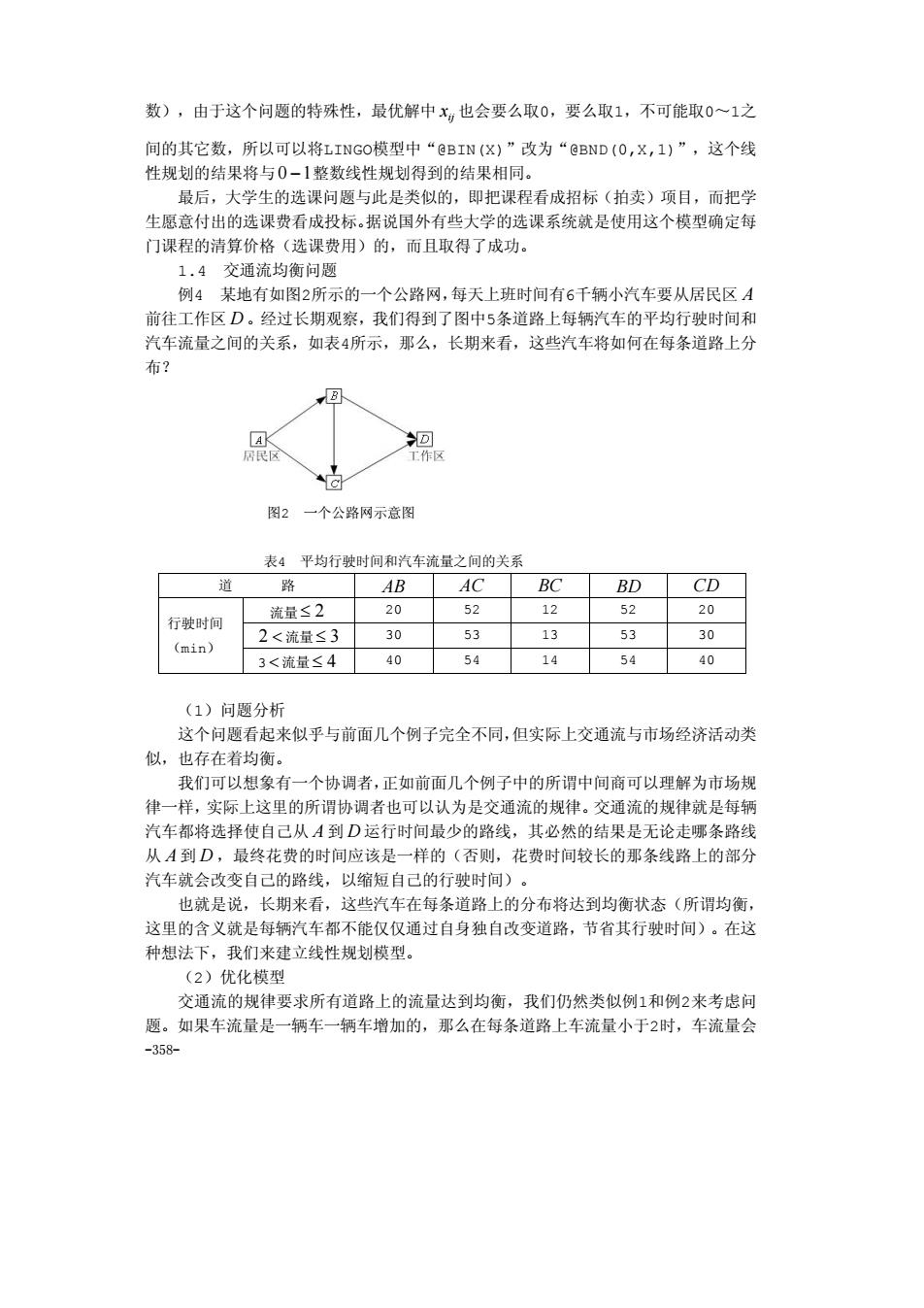
数),由于这个问题的特殊性,最优解中x也会要么取0,要么取1,不可能取0~1之 间的其它数,所以可以将LINGO模型中“@BIN(X)”改为“@BND(O,X,1)”,这个线 性规划的结果将与0-1整数线性规划得到的结果相同, 最后,大学生的选课问题与此是类似的,即把课程看成招标(拍卖)项目,而把学 生愿意付出的选课费看成投标。据说国外有些大学的选课系统就是使用这个模型确定每 门课程的清算价格(选课费用)的,而且取得了成功。 1,4交通流均有问题 例4某地有如图2所示的一个公路网,每天上班时间有6千辆小汽车要从居民区A 前往工作区D。经过长期观察,我们得到了图中5条道路上每辆汽车的平均行驶时间和 汽车流量之间的关系,如表4所示,那么,长期来看,这些汽车将如何在每条道路上分 布? 图2一个公路网示意图 表4平均行驶时间和汽车流量之间的关系 ABAC☐BC BD CD 流量≤2 20 52 12 52 20 行驶时间 2<流量≤3 30 53 13 53 30 (min) 3<流量≤4 40 14 54 40 (1)问题分析 这个问题看起来似乎与前面儿个例子完全不同,但实际上交通流与市场经济活动类 似,也存在着均衡。 我们 可以想象有一个协调者,正如前面几个例子中的所谓中间商可以理解为市场规 律一样,实际上这里的所谓协调者也可以认为是交通流的规律。交通流的规律就是每铜 汽车都将选择使自己从A到D运行时间最少的路线,其必然的结果是无论走哪条路线 从A到D,最终花费的时间应该是一样的(否则,花费时间较长的那条线路上的部分 汽车就会改变自己的路线,以缩短自己的行驶时间)。 也就是说, 长期来看 ,这些汽车在每条道路上的分布将达到均衡状态(所谓均衡, 这里的含义就是每辆汽车都不能仅仅通过自身独自改变道路,节省其行驶时间)。在这 种想法下,我们来建立线性规划模型。 (2)优化模型 交通流的规律要求所有道路上的流量达到均衡,我们仍然类似例1和例2来考虑问 题。如果车流量是一辆车一辆车增加的,那么在每条道路上车流量小于2时,车流量会 -358
-358- 数),由于这个问题的特殊性,最优解中 ij x 也会要么取0,要么取1,不可能取0~1之 间的其它数,所以可以将LINGO模型中“@BIN(X)”改为“@BND(0,X,1)”,这个线 性规划的结果将与0 −1整数线性规划得到的结果相同。 最后,大学生的选课问题与此是类似的,即把课程看成招标(拍卖)项目,而把学 生愿意付出的选课费看成投标。据说国外有些大学的选课系统就是使用这个模型确定每 门课程的清算价格(选课费用)的,而且取得了成功。 1.4 交通流均衡问题 例4 某地有如图2所示的一个公路网,每天上班时间有6千辆小汽车要从居民区 A 前往工作区 D 。经过长期观察,我们得到了图中5条道路上每辆汽车的平均行驶时间和 汽车流量之间的关系,如表4所示,那么,长期来看,这些汽车将如何在每条道路上分 布? 图2 一个公路网示意图 表4 平均行驶时间和汽车流量之间的关系 道 路 AB AC BC BD CD 流量 ≤ 2 20 52 12 52 20 2 < 流量 ≤ 3 30 53 13 53 30 行驶时间 (min) 3 < 流量 ≤ 4 40 54 14 54 40 (1)问题分析 这个问题看起来似乎与前面几个例子完全不同,但实际上交通流与市场经济活动类 似,也存在着均衡。 我们可以想象有一个协调者,正如前面几个例子中的所谓中间商可以理解为市场规 律一样,实际上这里的所谓协调者也可以认为是交通流的规律。交通流的规律就是每辆 汽车都将选择使自己从 A 到 D 运行时间最少的路线,其必然的结果是无论走哪条路线 从 A 到 D ,最终花费的时间应该是一样的(否则,花费时间较长的那条线路上的部分 汽车就会改变自己的路线,以缩短自己的行驶时间)。 也就是说,长期来看,这些汽车在每条道路上的分布将达到均衡状态(所谓均衡, 这里的含义就是每辆汽车都不能仅仅通过自身独自改变道路,节省其行驶时间)。在这 种想法下,我们来建立线性规划模型。 (2)优化模型 交通流的规律要求所有道路上的流量达到均衡,我们仍然类似例1和例2来考虑问 题。如果车流量是一辆车一辆车增加的,那么在每条道路上车流量小于2时,车流量会

有一个分布规律:当某条道路上流量正好超过2时,新加入的一辆车需要选择使自己堵 塞时间最短的道路。这就提示我们把同一条道路上的流量分布分解成不同性质的三个部 分。也就是说,我们用了(AB)表示道路AB上的总的流量,并进一步把它分解成三部 分: 1)道路AB上的流量不超过2时的流量,用X(2,AB)表示: 1i)道路AB上的流量超过2但不超过3时,超过2的流量部分用X(3,AB)表示: 1ii)道路AB上的流量超过3但不超过4时,超过3的流量部分用X(4,AB)表示 依次类推,对道路AC,BC,BD,CD上同理可以定义类似的决策变量。因此,问题 中总共有20个决策变量YU)和X(亿,)(i=2,3,4,j=AB,AC,BC,BD,CD)· 问题的目标应当是使总的堵塞时间最小。用T(,)表示流量X(亿,)对应的堵塞时 同(御表3中的据。是对钙车言的》,我看用三,作为 总堵塞时间是否合适。很容易理解:后面加入道路的车辆可能又会造成前面进入道路的 车辆的进一步堵塞,如流量为3时,原先流量为2的车辆实际上也只能按T(3,)的时间 通过,而不是T(2,)。也就是说,∑∑T亿,)X化,)并不是总堵塞时间。但是 我们也可以发现,T亿,)关于1是单调增加的,即不断增加的车流只会使以前的堵塞加 剧而不可能使以前的堵塞减缓。所以,关于决策变量X(化,)而言, 三高心刀与我们希望优化的目标的单调性是一货的因此可以用 三,刀X,刀作为目标函数进行优化· 约束条件有三类: 1)每条道路上的总流量Y等于该道路上的分流量X的和: i)道路交汇处A,B,C,D(一般称为节点)的流量守恒(即进入量等于流出量): iii)决策变量的上限限制,如X(2,AB)≤2,X(3,AB)≤1,X(4,AB)≤1等 于是对应的优化模型很容易直接写出(略)。 -359
-359- 有一个分布规律;当某条道路上流量正好超过2时,新加入的一辆车需要选择使自己堵 塞时间最短的道路。这就提示我们把同一条道路上的流量分布分解成不同性质的三个部 分。也就是说,我们用Y(AB) 表示道路 AB 上的总的流量,并进一步把它分解成三部 分: i)道路 AB 上的流量不超过2时的流量,用 X (2, AB) 表示; ii)道路 AB 上的流量超过2但不超过3时,超过2的流量部分用 X (3, AB) 表示; iii)道路 AB 上的流量超过3但不超过4时,超过3的流量部分用 X (4, AB) 表示。 依次类推,对道路 AC, BC, BD,CD 上同理可以定义类似的决策变量。因此,问题 中总共有20个决策变量Y( j) 和 X (i, j)(i = 2,3,4 , j = AB, AC, BC, BD,CD )。 问题的目标应当是使总的堵塞时间最小。用T(i, j) 表示流量 X (i, j)对应的堵塞时 间(即表3中的数据,是对每辆车而言的),我们看看用 ∑ ∑ =2,3,4 ( , ) ( , ) i j T i j X i j 为道路 作为 总堵塞时间是否合适。很容易理解:后面加入道路的车辆可能又会造成前面进入道路的 车辆的进一步堵塞,如流量为3时,原先流量为2的车辆实际上也只能按T(3, j) 的时间 通过,而不是T(2, j) 。也就是说, ∑ ∑ =2,3,4 ( , ) ( , ) i j T i j X i j 为道路 并不是总堵塞时间。但是 我们也可以发现,T(i, j) 关于i 是单调增加的,即不断增加的车流只会使以前的堵塞加 剧而不可能使以前的堵塞减缓。所以,关于决策变量 X (i, j) 而言, ∑ ∑ =2,3,4 ( , ) ( , ) i j T i j X i j 为道路 与我们希望优化的目标的单调性是一致的。因此,可以用 ∑ ∑ =2,3,4 ( , ) ( , ) i j T i j X i j 为道路 作为目标函数进行优化。 约束条件有三类: i)每条道路上的总流量Y 等于该道路上的分流量 X 的和; ii)道路交汇处 A, B,C, D(一般称为节点)的流量守恒(即进入量等于流出量); iii)决策变量的上限限制,如 X (2, AB) ≤ 2 ,X (3, AB) ≤1,X (4, AB) ≤1等。 于是对应的优化模型很容易直接写出(略)

(3)模型求解 编写LINGO程序如下: MODEL: TITLE通 SETS: ROAD/AB,AC,BC,BD,CD/:Y; CAR/2,3,4/: LINK (CAR.ROAD):T.X: ENDSETS DATA: !行玻时向(分钟) T=20,52,12,52,20 30,53,13,53,30 40,54,14,54,40 ENDDATA IOBJ1MIN=@SUM(LINK:T*K):!日标&款 !四个节点的流量守恒缘件: [NODE_A]Y(@INDEX (AB))+Y(@INDEX (AC))=6; [NODE_B]Y(@INDEX(AB))=Y(@INDEX (BC))+Y(@INDEX(BD) [NODE_C]Y(@INDEX (AC))+Y (@INDEX(BC))=Y(@INDEX (CD)) 【NODE_D】Y(BINDEX(BD)+Y(@INDEX(CD)-6 !每条道路上的总流量Y等于该道路上的分流量X的和: @FOR(ROAD(I)[ROAD_LIM]@SUM(CAR(J):x(J,I))=Y(I)); 1盒会懂路的合范餐X的上下界设空: @FOR(LINK(I,J)II#EQ#1:@BND(0,X(I,J),2) END 可以指出的是,上面4个节点的流量守恒条件中,其实只有3个是独立的(也就是 说,第4个条件总可以从其它3个方程推导出来),因此从中去掉任何一个都不会影响 到计算结果。 (4)结果解释 LINGO的运行结果表明,均衡时道路AB,AC,BC,BD,CD的流量分别是4,2,2, 2,4(千辆)车。但是要注意,正如我们建立目标函数时所讨论过的,这时得到的目 标函数值452并不是真正的总运行和堵塞时间,而是一个用来表示目标函数趋势的虚拟 的量,没有太多实际物理意义。事实上,可以求出这时的真正运行时间是:每辆车通过 AB,AC,BC,BD,CD道路分别需要40,52,12,52,40(min),也就是在图中 -360
-360- (3)模型求解 编写LINGO程序如下: MODEL: TITLE 交通流均衡; SETS: ROAD/AB,AC,BC,BD,CD/:Y; CAR/2,3,4/; LINK(CAR,ROAD): T, X; ENDSETS DATA: ! 行驶时间(分钟) ; T=20,52,12,52,20 30,53,13,53,30 40,54,14,54,40; ENDDATA [OBJ] MIN=@SUM(LINK: T*X); ! 目标函数; ! 四个节点的流量守恒条件; [NODE_A] Y(@INDEX(AB))+Y(@INDEX(AC)) = 6; [NODE_B] Y(@INDEX(AB))=Y(@INDEX(BC))+Y(@INDEX(BD)); [NODE_C] Y(@INDEX(AC))+Y(@INDEX(BC))=Y(@INDEX(CD)); [NODE_D] Y(@INDEX(BD))+Y(@INDEX(CD))=6; ! 每条道路上的总流量Y等于该道路上的分流量X的和; @FOR( ROAD(I): [ROAD_LIM] @SUM(CAR(J): X(J,I)) = Y(I)); ! 每条道路的分流量X的上下界设定; @FOR(LINK(I,J)|I#EQ#1: @BND(0,X(I,J),2) ); @FOR(LINK(I,J)|I#GT#1: @BND(0,X(I,J),1) ); END 可以指出的是,上面4个节点的流量守恒条件中,其实只有3个是独立的(也就是 说,第4个条件总可以从其它3个方程推导出来),因此从中去掉任何一个都不会影响 到计算结果。 (4)结果解释 LINGO的运行结果表明,均衡时道路 AB, AC, BC, BD,CD 的流量分别是4,2,2, 2,4(千辆)车。但是要注意,正如我们建立目标函数时所讨论过的,这时得到的目 标函数值452并不是真正的总运行和堵塞时间,而是一个用来表示目标函数趋势的虚拟 的量,没有太多实际物理意义。事实上,可以求出这时的真正运行时间是:每辆车通过 AB, AC, BC, BD,CD 道路分别需要40,52,12,52,40(min),也就是在图中三