
第十九章神经网络模型 S1神经网络简介 防能的神经网络是在现代神经科学的基瑞上提出和发展起来的,肯在反碳人脑药构 象数学模 模型以 经网络理论技术 204 究取得 界 机 40多 种神经网络使理 甘d 较若名的有感 知机,Hopfield网络,Boltzman机,自适应共振理论及反向传播网络(BP)等。在这 里我们仅讨论最基木的网络模型及其学习算法。 11人工神经元揽型 下图表示出了作为人工神经网络(artificial neural network,以下简称NN)的基本 单元的神经元模型,它有三个基本要素: 激活函数 一输出 求和 。气m 阙值 连接权 ()一组连接(对应于生物神经元的突触),连接强度由各连接上的权值表示,权 值为正表示激活,为负表示抑制。 ()一个求和单元,用于求取各输入信号的加权和(线性组合)。 ()一个非线性激活函数,起非线性映射作用并将神经元输出幅度限制在一定范 围内(一般限制在(0,1)或(-1,1)之间)。 此外还有一个阈值0(或偏置b=-0)。 以上作用可分别以数学式表达出来: 4=∑wx,=w4-0,y4=0y) 式中x1,x2,x,为输入信号,w1,W2,w为神经元k之权值,山,为线性组合编结 果,A为阈值,p()为激活函数,:为神经元k的输出。 若把输入的维数增加一维,则可把阅值O包括进去。例如 之"g,h=pu4) 此处增加了一个新的连接,其输入为x,=-1(或+1),权值为=日(或),如 下图所示。 -230-
-230- 第十九章 神经网络模型 §1 神经网络简介 人工神经网络是在现代神经科学的基础上提出和发展起来的,旨在反映人脑结构及 功能的一种抽象数学模型。自 1943 年美国心理学家 W. McCulloch 和数学家 W. Pitts 提 出形式神经元的抽象数学模型—MP 模型以来,人工神经网络理论技术经过了 50 多年 曲折的发展。特别是 20 世纪 80 年代,人工神经网络的研究取得了重大进展,有关的理 论和方法已经发展成一门界于物理学、数学、计算机科学和神经生物学之间的交叉学科。 它在模式识别,图像处理,智能控制,组合优化,金融预测与管理,通信,机器人以及 专家系统等领域得到广泛的应用,提出了 40 多种神经网络模型,其中比较著名的有感 知机,Hopfield 网络,Boltzman 机,自适应共振理论及反向传播网络(BP)等。在这 里我们仅讨论最基本的网络模型及其学习算法。 1.1 人工神经元模型 下图表示出了作为人工神经网络(artificial neural network,以下简称 NN)的基本 单元的神经元模型,它有三个基本要素: (i)一组连接(对应于生物神经元的突触),连接强度由各连接上的权值表示,权 值为正表示激活,为负表示抑制。 (ii)一个求和单元,用于求取各输入信号的加权和(线性组合)。 (iii)一个非线性激活函数,起非线性映射作用并将神经元输出幅度限制在一定范 围内(一般限制在(0,1) 或(−1,1) 之间)。 此外还有一个阈值θ k (或偏置bk = −θ k )。 以上作用可分别以数学式表达出来: ∑= = p j k kj j u w x 1 , k uk k v = −θ , ( ) k k y = ϕ v 式中 p x , x , , x 1 2 L 为输入信号, wk wk wkp , , , 1 2 L 为神经元 k 之权值,uk 为线性组合结 果,θ k 为阈值,ϕ(⋅) 为激活函数, k y 为神经元k 的输出。 若把输入的维数增加一维,则可把阈值θ k 包括进去。例如 ∑= = p j k kj j v w x 0 , ( ) k uk y = ϕ 此处增加了一个新的连接,其输入为 x0 = −1(或 +1),权值为 wk 0 = θ k (或bk ),如 下图所示
国定输人 x10 激活函数 雀语函数 】 求和 和 连接权 连接权 激活函数()可以有以下几种: ()铜值函数 )=≥0 (0,v<0 (1) 即阶梯函数。这时相应的输出y:为 1,20 其中,=,-日.,蒂称此种神经元为M-P模型, ()分段线性函数 y≥1 p)=51+,-1<v<1 (2) 2 0. v≤-1 1的非线性放大器,当工作于线性区时它是一个线性组合器 最常用的函数形式为 (v)= (3 1+exp(-an) 参数α>0可控制其斜率。另一种常用的是双曲正切函数 (v)=tanh=1-exp(-v) (4) 21+exp(-v) 这类函数具有平滑和近 性 线性传通函 -231
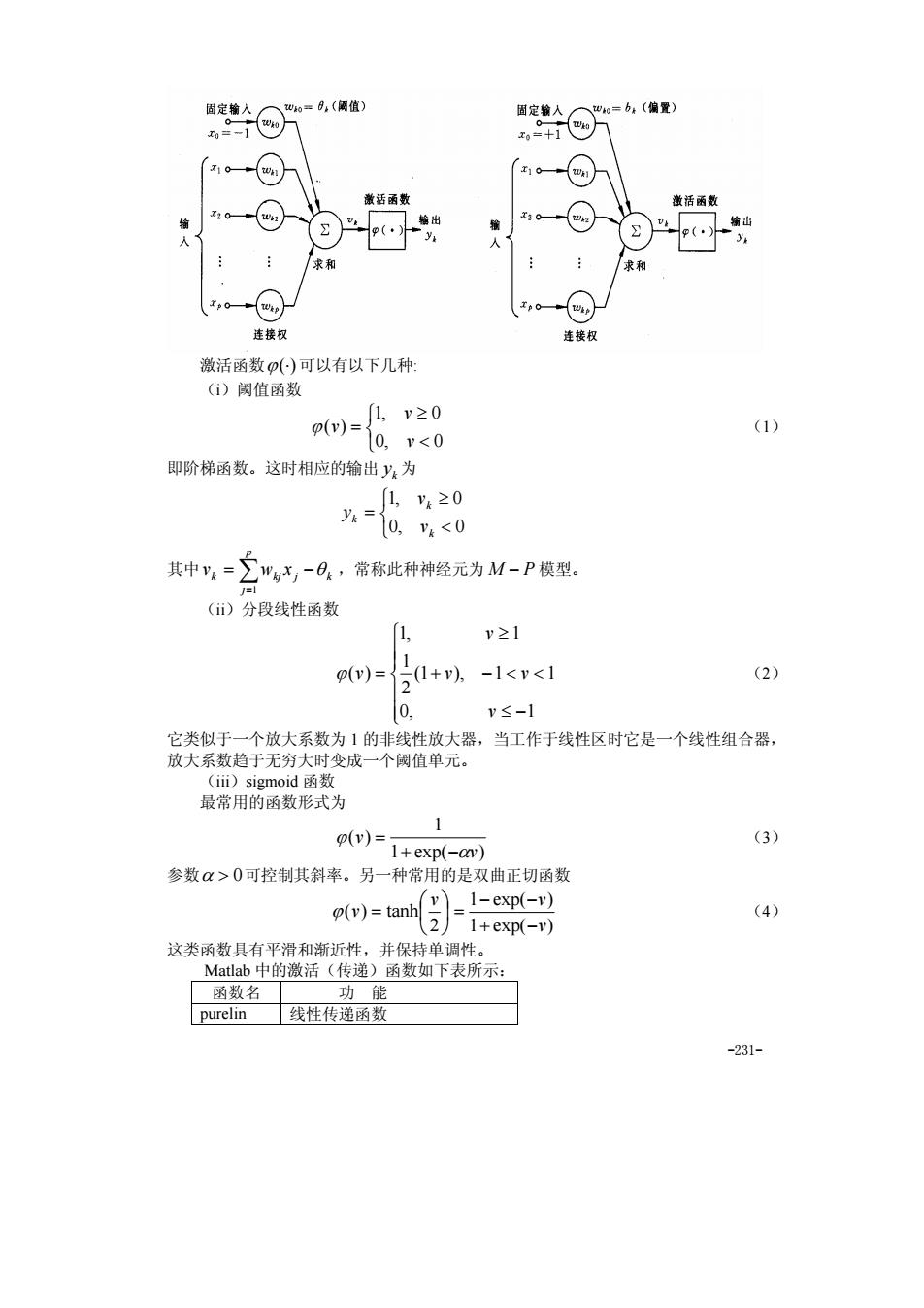
-231- 激活函数ϕ(⋅) 可以有以下几种: (i)阈值函数 ⎩ ⎨ ⎧ < ≥ = 0, 0 1, 0 ( ) v v ϕ v (1) 即阶梯函数。这时相应的输出 k y 为 ⎩ ⎨ ⎧ < ≥ = 0, 0 1, 0 k k k v v y 其中 ∑= = − p j k kj j k v w x 1 θ ,常称此种神经元为 M − P 模型。 (ii)分段线性函数 ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ≤ − + − < < ≥ = 0, 1 (1 ), 1 1 2 1 1, 1 ( ) v v v v ϕ v (2) 它类似于一个放大系数为 1 的非线性放大器,当工作于线性区时它是一个线性组合器, 放大系数趋于无穷大时变成一个阈值单元。 (iii)sigmoid 函数 最常用的函数形式为 1 exp( ) 1 ( ) v v α ϕ + − = (3) 参数α > 0可控制其斜率。另一种常用的是双曲正切函数 1 exp( ) 1 exp( ) 2 ( ) tanh v v v v + − − − ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ ϕ = (4) 这类函数具有平滑和渐近性,并保持单调性。 Matlab 中的激活(传递)函数如下表所示: 函数名 功 能 purelin 线性传递函数

hardlim硬限幅传递函数 hardlims对称硬限幅传递函数 satlin 饱和线性传递函 satlins 对称饱和线性传递函数 logsig 数S形传递函货 正切S形传 radbas compet克争层传递函数 各个函数的定义及使用方法,可以参看Matlab的帮助(如在Matlab命令窗口运行 help tansig,可以看到tantig的使用方法, 及ne的定义为p)1+e-1》 ,於单网络信枸及孩结的也是的一个要特性·从连接方式有NN主多 ()前情型网终 各神经元接受前一层的输入,并输出给下一层,没有反馈。结点分为两类,即输入 单元和计算单元,每一计算单元可有任意个输入,但贝有一个输出(它可耦合到任意多 个其它结点作为其输入)。通常前馈网络可分为不同的层,第i层的输入只与第1-1层 输出相连,输入和输出结点与外界相连,而其它中间层则称为隐层。 ()反馈型树绍 所有结点都是计算单元,同时也可接受输入,并向外界输出 NN的I 程王 期此 从作用效果看,前馈网络主要是函数映射,可用于模式识别和函数逼近。反馈网络 按对能最函数的极小点的利用来分类有两种:第一类是能量函数的 所有极小点都起 用,这一类主要用作各种联想存储器:第二类只利用全局极小点,它主要用于求解最优 化问题。 §2蠓虫分类问题与多层前馈网络 依据的资 问题 (Ar )进行鉴别, Af124,1270 13617 381 ,(138 0 140,1.70) 1481g21/154121/15620g 2816.a2126202820301 ()根据如上资料,如何制定一种方法,正确地区分两类蠓虫。 (ii)对触角和翼长分别为1.24,1.80),(1.28,1.84)与(1.40,2.04)的3个标本,用所得 到的方法加以识别 宝贵的传粉益虫,Apf是某 无柄的载体 是否哑咳修改分万法 (9支Af的数据和6 -232-
-232- hardlim 硬限幅传递函数 hardlims 对称硬限幅传递函数 satlin 饱和线性传递函数 satlins 对称饱和线性传递函数 logsig 对数 S 形传递函数 tansig 正切 S 形传递函数 radbas 径向基传递函数 compet 竞争层传递函数 各个函数的定义及使用方法,可以参看 Matlab 的帮助(如在 Matlab 命令窗口运行 help tansig,可以看到 tantig 的使用方法,及 tansig 的定义为 1 1 2 ( ) 2 − + = − v e ϕ v )。 1.2 网络结构及工作方式 除单元特性外,网络的拓扑结构也是 NN 的一个重要特性。从连接方式看 NN 主要 有两种。 (i)前馈型网络 各神经元接受前一层的输入,并输出给下一层,没有反馈。结点分为两类,即输入 单元和计算单元,每一计算单元可有任意个输入,但只有一个输出(它可耦合到任意多 个其它结点作为其输入)。通常前馈网络可分为不同的层,第i 层的输入只与第i −1层 输出相连,输入和输出结点与外界相连,而其它中间层则称为隐层。 (ii)反馈型网络 所有结点都是计算单元,同时也可接受输入,并向外界输出。 NN 的工作过程主要分为两个阶段:第一个阶段是学习期,此时各计算单元状态不 变,各连线上的权值可通过学习来修改;第二阶段是工作期,此时各连接权固定,计算 单元状态变化,以达到某种稳定状态。 从作用效果看,前馈网络主要是函数映射,可用于模式识别和函数逼近。反馈网络 按对能量函数的极小点的利用来分类有两种:第一类是能量函数的所有极小点都起作 用,这一类主要用作各种联想存储器;第二类只利用全局极小点,它主要用于求解最优 化问题。 §2 蠓虫分类问题与多层前馈网络 2.1 蠓虫分类问题 蠓虫分类问题可概括叙述如下:生物学家试图对两种蠓虫(Af 与 Apf)进行鉴别, 依据的资料是触角和翅膀的长度,已经测得了 9 支 Af 和 6 支 Apf 的数据如下: Af: (1.24,1.27),(1.36,1.74),(1.38,1.64),(1.38,1.82),(1.38,1.90),(1.40,1.70), (1.48,1.82),(1.54,1.82),(1.56,2.08). Apf: (1.14,1.82),(1.18,1.96),(1.20,1.86),(1.26,2.00),(1.28,2.00),(1.30,1.96). 现在的问题是: (i)根据如上资料,如何制定一种方法,正确地区分两类蠓虫。 (ii)对触角和翼长分别为(1.24,1.80),(1.28,1.84)与(1.40,2.04)的 3 个标本,用所得 到的方法加以识别。 (iii)设 Af 是宝贵的传粉益虫,Apf 是某疾病的载体,是否应该修改分类方法。 如上的问题是有代表性的,它的特点是要求依据已知资料(9 支 Af 的数据和 6 支 Apf 的数据)制定一种分类方法,类别是已经给定的(Af 或 Apf)。今后,我们将 9 支

Af及6支Apf的数据集合称之为学习样本。 为解上述问透,考忠一个其结构如下图所示的人工神经网络 0 激活函数由 1 ()= 图中曼下面 1+exp(-av) ,即 不的 一层 用以品 中的 包 理月 的选取 进行了讨论 有 试验来次定我的例中只 个就足 「层称为输出层 ,或许是最好的途径 在我 用以输出与每一组输 数据相对应的分类信息.任何一个中间层单元接受所有输入单元传来的信号,并把处理 后的结果传向每一个输出单元,供输出层再次加工,同层的神经元彼此不相联接,输入 与输出单元之间也没有直接联接。这样,除了神经元的形式定义外,我们又给出了网络 结构。有些文献将这样的网络称为两层前传网络,称为两层的理由是,只有中间层及输 出层的单元才对信号进行处理:输入层的单元对输入数据没有任何加工,故不计算在层 数之 了叙述上的方便,此处引人如下记号上的约定 令5表示 个确定的已知样品转 号,在蠓虫问题中,s=1,2,.,15,分别表示学习样本中的15个样品:当将第3个样 品的原始数据输入网络时,相应的输出单元状态记为O(1=1,2),隐单元状态记为 HU=12,3),输入单元取值记为(化=1,2)。请注意,此处下标1,j,k依次对应于 输出层、中间层及输入层。在这一约定下,从中间层到输出层的权记为,从输入层 到中间层的权记为亚:·如果”,亚:均己给定,那么,对应于任何一组确定的输入 (,),网络中所有单元的取值不难确定。事实上,对样品s而言,隐单元广的输入 是 形=∑平k月 (5) 相应的输出状态是 H=p(i)=p(∑币) (6) 由此,输出单元i所接收到的迭加信号是 -233
-233- Af 及 6 支 Apf 的数据集合称之为学习样本。 2.2 多层前馈网络 为解决上述问题,考虑一个其结构如下图所示的人工神经网络, 激活函数由 1 exp( ) 1 ( ) v v α ϕ + − = 来决定。图中最下面单元,即由•所示的一层称为输入层,用以输入已知测量值。在 我们的例子中,它只需包括两个单元,一个用以输入触角长度,一个用以输入翅膀长度。 中间一层称为处理层或隐单元层,单元个数适当选取,对于它的选取方法,有一些文献 进行了讨论,但通过试验来决定,或许是最好的途径。在我们的例子中,取三个就足够 了。最上面一层称为输出层,在我们的例子中只包含二个单元,用以输出与每一组输入 数据相对应的分类信息.任何一个中间层单元接受所有输入单元传来的信号,并把处理 后的结果传向每一个输出单元,供输出层再次加工,同层的神经元彼此不相联接,输入 与输出单元之间也没有直接联接。这样,除了神经元的形式定义外,我们又给出了网络 结构。有些文献将这样的网络称为两层前传网络,称为两层的理由是,只有中间层及输 出层的单元才对信号进行处理;输入层的单元对输入数据没有任何加工,故不计算在层 数之内。 为了叙述上的方便,此处引人如下记号上的约定:令 s 表示一个确定的已知样品标 号,在蠓虫问题中, s = 1,2,L,15,分别表示学习样本中的 15 个样品;当将第 s 个样 品的原始数据输入网络时,相应的输出单元状态记为O (i = 1,2) s i ,隐单元状态记为 H ( j = 1,2,3) s j ,输入单元取值记为 I (k = 1,2) s k 。请注意,此处下标i, j,k 依次对应于 输出层、中间层及输入层。在这一约定下,从中间层到输出层的权记为 wij ,从输入层 到中间层的权记为 wjk 。如果 wij , wjk 均已给定,那么,对应于任何一组确定的输入 ( , ) 1 2 s s I I ,网络中所有单元的取值不难确定。事实上,对样品 s 而言,隐单元 j 的输入 是 ∑= = 2 k 1 s jk k s j h w I (5) 相应的输出状态是 ∑= = = 2 1 ( ) ( ) k s jk k s j s j H ϕ h ϕ w I (6) 由此,输出单元i 所接收到的迭加信号是

龙=∑w,H;=∑w,p(∑而I) (7) 网络的最终输出是 O=h)=p(∑w,H)=(∑w,p(∑wk/)》 (8) 这里,没有考虑阔值,正如前面已经说明的那样,这一点是无关紧要的。还应指出的是, 对于任何一组确定的输入,输出是所有权{w,亚}的函数。 如果我们能够选定一组适当的权值{w,币},使得对应于学习样本中任何一组A 样品的输入(I,I),输出(O,O)=(1,0),对应于Apf的输入数据,输出为(0,1), 那么蠓虫分类问题实际上就解决了。因为,对于任何一个未知类别的样品,只要将其触 角及翅膀长度输入网络,视其输出模式靠近(1,0)亦或(0,1),就可能判断其归属。当然, 2.3向后传播算法 对于一个多层网络,如何求得一组恰当的权值,使网络具有特定的功能,在很长 段时间内,曾经是使研究工作者感到困难的一个问题,直到1985年,美国加州大学的 个研究小组提出了所谓向后传播算法(Back-Propagation),使问题有了重大进展,这 一算法也是促成人工神经网络研究迅猛发展的一 个原因。下面就来介绍这一算法。 如前所述,我们希望对应于学习样本中Af样品的输出是(1,O),对应于Apf的输出 是(0,),这样的输出称之为理想输出。实际上要精确地作到这一点是不可能的,只能 希望实际输出尽可能地接近理想输出。为清楚起见,把对应于样品S的理想输出记为 T,那么 E0w)=ΣT-0) (9) E(W)=∑IT-p(,p20川 (10) 易知,对每一个变量W,或币而言,这是一个连续可微的非线性函数,为了求得其极 小点与极小值,最为方便的就是使用最速下降法。最速下降法是一种迭代算法,为求出 E(W)的(局部)极小,它从一个任取的初始点。出发,计算在W。点的负梯度方向 一VE(W。),这是函数在该点下降最快的方向:只要E(W。)≠0,就可沿该方向移动 一小段距离,达到一个新的点用=。-NE(W。),刀是一个参数,只要n足够小, 定能保证E(W)<E(W)。不断重复这一过程,一定能达到E的一个(局部)极小点。 就本质而言,这就是B即算法的全部内容,然而,对人工神经网络问题而言,这一算法 的具体形式是非常重要的,下面我们就来给出这一形式表达。 对于隐单元到输出单元的权”,而言,最速下降法给出的每一步的修正量是 -234-
-234- ∑ ∑∑ = == = = 3 1 3 1 2 1 ( ) j jk s ij jk k s ij j s i h w H w ϕ w I (7) 网络的最终输出是 ( ) ( ) ( ( )) 3 1 2 1 3 1 ∑ ∑ ∑ = = = = = = j k s ij jk k j s ij j s i s i O ϕ h ϕ w H ϕ w ϕ w I (8) 这里,没有考虑阈值,正如前面已经说明的那样,这一点是无关紧要的。还应指出的是, 对于任何一组确定的输入,输出是所有权{ , } wij wjk 的函数。 如果我们能够选定一组适当的权值{ , } wij wjk ,使得对应于学习样本中任何一组 Af 样品的输入( , ) 1 2 s s I I ,输出( , ) (1,0) 1 2 = s s O O ,对应于 Apf 的输入数据,输出为(0,1) , 那么蠓虫分类问题实际上就解决了。因为,对于任何一个未知类别的样品,只要将其触 角及翅膀长度输入网络,视其输出模式靠近(1,0) 亦或(0,1) ,就可能判断其归属。当然, 有可能出现介于中间无法判断的情况。现在的问题是,如何找到一组适当的权值,实现 上面所设想的网络功能。 2.3 向后传播算法 对于一个多层网络,如何求得一组恰当的权值,使网络具有特定的功能,在很长一 段时间内,曾经是使研究工作者感到困难的一个问题,直到 1985 年,美国加州大学的 一个研究小组提出了所谓向后传播算法(Back-Propagation),使问题有了重大进展,这 一算法也是促成人工神经网络研究迅猛发展的一个原因。下面就来介绍这一算法。 如前所述,我们希望对应于学习样本中 Af 样品的输出是(1,0) ,对应于 Apf 的输出 是(0,1) ,这样的输出称之为理想输出。实际上要精确地作到这一点是不可能的,只能 希望实际输出尽可能地接近理想输出。为清楚起见,把对应于样品 s 的理想输出记为 { } s Ti ,那么 = ∑ − i s s i s E W Ti O , 2 ( ) 2 1 ( ) (9) 度量了在一组给定的权下,实际输出与理想输出的差异,由此,寻找一组恰当的权的问 题,自然地归结为求适当W 的值,使 E(W ) 达到极小的问题。将式(8)代入(9),有 ∑ ∑∑ = = = − s jk i s ij jk k s i E W T w w I , 2 3 1 2 1 [ ( ( ))] 2 1 ( ) ϕ ϕ (10) 易知,对每一个变量 wij 或 wij 而言,这是一个连续可微的非线性函数,为了求得其极 小点与极小值,最为方便的就是使用最速下降法。最速下降法是一种迭代算法,为求出 E(W ) 的(局部)极小,它从一个任取的初始点W0 出发,计算在W0 点的负梯度方向 — ( ) ∇E W0 ,这是函数在该点下降最快的方向;只要∇E(W0 ) ≠ 0 ,就可沿该方向移动 一小段距离,达到一个新的点 ( ) W1 = W0 −η∇E W0 ,η 是一个参数,只要η 足够小, 定能保证 ( ) ( ) E W1 < E W0 。不断重复这一过程,一定能达到 E 的一个(局部)极小点。 就本质而言,这就是 BP 算法的全部内容,然而,对人工神经网络问题而言,这一算法 的具体形式是非常重要的,下面我们就来给出这一形式表达。 对于隐单元到输出单元的权 wij 而言,最速下降法给出的每一步的修正量是