
Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material 方差分析的基本思想 方差分析的依据是建立在变差平方和具有加和性的 基础上的。因此,如果用变差平方和来表征测定猪 果的总变差,那么总变差的平方和就等于各变异因 素形成的变差平方和的总和。 方差分析的基本思想,就是将总变差分解为各构成 部分之和,然后对它们作统计检验。总变差: SS=∑∑(X,-)2 i=1i=1 其中m为试验水平数,n为重复次数,自由度vT= mn-1=W-1 振华制 数理统计在化学中的应用
李 振 华 制 数理统计在化学中的应用 造 方差分析的基本思想 ◼ 方差分析的依据是建立在变差平方和具有加和性的 基础上的。因此,如果用变差平方和来表征测定结 果的总变差,那么总变差的平方和就等于各变异因 素形成的变差平方和的总和。 ◼ 方差分析的基本思想,就是将总变差分解为各构成 部分之和,然后对它们作统计检验。总变差: 其中m为试验水平数,n为重复次数,自由度vT = mn – 1 = N – 1 2 1 1 ( ) m n T ij i j SS X X = = = −

Center for Theoretical Chemical Physics Laboratory of molecular Catalysis innovative material 9 条件变差(组间方差) 每一组的测定平怕值和总平怕值差值的平方和再乘 以重复次数 SS4=n(,-)} i1 自由度vA=m-1 李振华 数理统计在化学中的应用 造
李 振 华 制 数理统计在化学中的应用 造 条件变差(组间方差) ◼ 每一组的测定平均值和总平均值差值的平方和再乘 以重复次数: 自由度vA = m – 1 2 1 ( ) m A i i SS n X X = = −

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 试验误差(组内方差) ■各组内的每次测定值和组内平怕值差值的平方和: 177 SS=∑∑(X,-,)》月 i=1j=1 自由度ye=m(n-1)=N-m 李振华制 数理统计在化学中的应用
李 振 华 制 数理统计在化学中的应用 造 试验误差(组内方差) ◼ 各组内的每次测定值和组内平均值差值的平方和: 自由度ve = m(n – 1) = N – m 2 1 1 ( ) m n e ij i i j SS X X = = = −

Center for Theoretical Chemical Physics Laboratory of molecular Catalysis innovative material 总变差的分解 5S4=n2(区,-X2 5S.=∑∑(X,-x,) 1= i=1 j=1 SS,=∑∑(X,-x=∑∑(X,-,)+(,-X i- =∑2(X,-)2+∑∑(,-+2∑∑(X,-X,x,-) i=1j=1 i=1 i=l i=1 i=l 22X,-+(x-X+2(,-x,-,) i=1j=1 i=1 i=1 SS,=∑∑(X,-X,)+22(元,-X i=1 i=1 i=l =SS4+SS。 李振华 数理统计在化学中的应用 造
李 振 华 制 数理统计在化学中的应用 造 总变差的分解 2 1 ( ) m A i i SS n X X = = − 2 2 1 1 1 1 2 2 1 1 1 1 1 1 2 2 1 1 1 1 1 1 ( ) [( ) ( )] ( ) ( )] 2 ( )( ) ( ) ( ) 2 ( ) ( ) m n m n T ij ij i i i i i j m n m n m n ij i i ij i i i j i j i j m n m n m n ij i i i ij i i j i j i j SS X X X X X X X X X X X X X X X X X X X X X X = = = = = = = = = = = = = = = = = − = − + − = − + − + − − = − + − + − − 2 2 1 1 1 1 ( ) ( )] m n m n T ij i i i j i j A e SS X X X X SS SS = = = = = − + − = + 2 1 1 ( ) m n e ij i i j SS X X = = = −
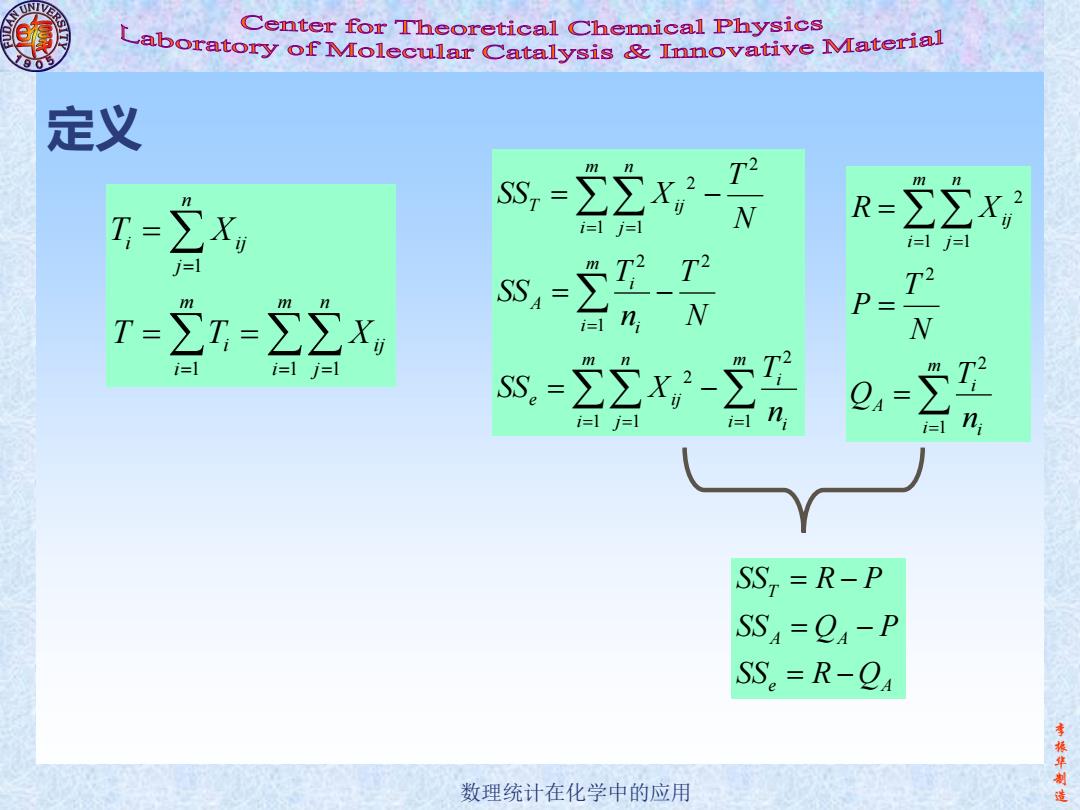
Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 定义 n I=∑x, i=1 j=1 N R= ∑∑x, i=1 i=l r-,=22x, s,- 2_ P= i=l n N i=1i= 拉网 4= i=1 j=1 i=l 得 SS,=R-P SS=O4-P SS。=R-Qa 数理统计在化学中的应用 李振华制造
李 振 华 制 数理统计在化学中的应用 造 定义 1 1 1 1 n i ij j m m n i ij i i j T X T T X = = = = = = = 2 2 1 1 2 2 1 2 2 1 1 1 m n T ij i j m i A i i m n m i e ij i j i i T SS X N T T SS n N T SS X n = = = = = = = − = − = − 2 1 1 2 2 1 m n ij i j m i A i i R X T P N T Q n = = = = = = T A A e A SS R P SS Q P SS R Q = − = − = −