
第三章! 实验数据的参数估计
数理统计在化学中的应用 第三章 实验数据的参数估计

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis&Inovative Material $3.1.2:期笔值的算规时 1.E(x)=lim =u (3-1) n D(x)=E[(x-u)2] (3-2) 2.E(a)=lim na a (3-3) n n D(a=E[(a-a)2]=0 (3-4) 3.E(ax)=a E(x) (3-5) D(ax)=a2 D(x) (3-6) 4.E(∑x)=∑E(x)=u (3-7) D(∑x,)=∑D(x)=nD(x)=no2 (3-8) 振华制 数理统计在化学中的应用
李 振 华 制 数理统计在化学中的应用 造 $3.1.2: 期望值的运算规则 2 1. ( ) lim (3-1) ( ) [( - ) ] (3- 2) 2. ( ) lim x E x n D x E x a na E a a n n 2 2 (3-3) ( ) [( - ) ] 0 (3- 4) 3. ( ) ( ) (3-5) ( ) ( ) D a E a a E ax a E x D ax a D x 2 (3-6) 4. ( ) ( ) (3-7) ( ) ( ) ( ) (3-8) i i E x E x n D x D x n D x n
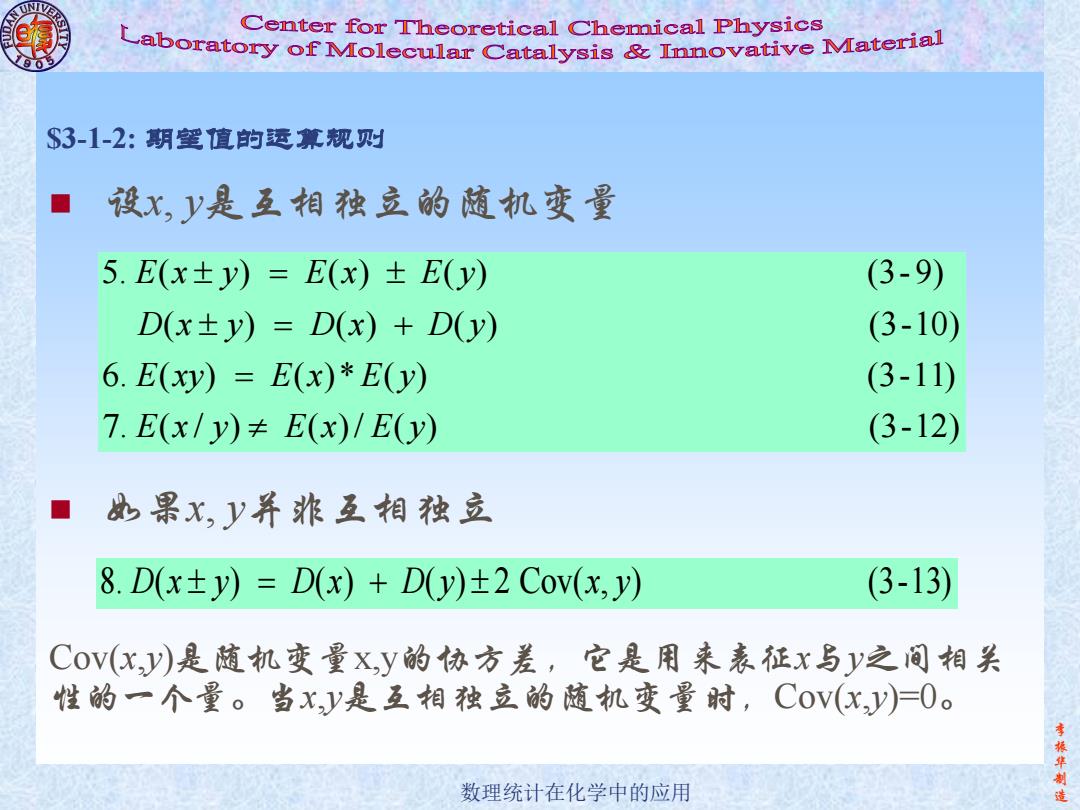
Center for Theoretical Chemical Physics poratory of molecular Catalysis innovative mater S3-1-2:期望值的透算规对 设x,y是互相独立的随机变量 5.E(x±y)=E(x)±E(y) (3-9) D(x±y)=D(x)+D(y) (3-10) 6.E(xy)=E(x)*E(y) (3-11) 7.E(x/y)≠E(x)/E(y) (3-12) 如果x,y并非互相独立 8.D(x±y)=D(x)+D(y)±2Cov(x,y) (3-13) CoV(x,y)是随机变量X,y的依方差,它是用来表征x与y之间相关 性的一个量。当x,y是互相独立的随机变量时,C0V(x)=0。 振华 数理统计在化学中的应用 造
李 振 华 制 数理统计在化学中的应用 造 $3-1-2: 期望值的运算规则 5. ( ) ( ) ( ) (3-9) ( ) ( ) ( ) (3-10) 6. ( ) ( )* ( ) E x y E x E y D x y D x D y E xy E x E y (3-11) 7. ( / ) ( ) / ( ) E x y E x E y (3-12) 设x, y是互相独立的随机变量 如果x, y并非互相独立 8. ( ) ( ) ( ) 2 Cov( , ) D x y D x D y x y (3-13) Cov(x,y)是随机变量x,y的协方差,它是用来表征x与y之间相关 性的一个量。当x,y是互相独立的随机变量时,Cov(x,y)=0

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 90 $3.1.3:几个重要的关系 62 D(ax)a2 D(x) D) n Dx=X)-Σ列-∑D刻 nD(x)=D( 1 n n n 李振华 数理统计在化学中的应用 造
李 振 华 制 数理统计在化学中的应用 造 $3.1.3: 几个重要的关系 2 D x( ) = n 2 2 2 2 1 1 ( ) ( ) ( ) ( ) 1 ( ) ( ) x D x D D x D x n n n D x nD x n n n 2 D ax a D x ( ) ( )

e Center for Theoretical Chemical Physics FMolecular Catalysis&及Innov分 学生分布 z X-u o/√n T= X-a SIn 李振华 数理统计在化学中的应用 造
李 振 华 制 数理统计在化学中的应用 造 学生分布 / X n T S n / Xn Z n