
例3.2.11 设m(t为正弦信号,进行100%的幅度调制,求 此时的调制效率。 解:依题意可设(t)=Am cos @mt 而100%调制就是A,=|m()max的调制,即A,=Am 因此 m2(0 2 2 m2(t) n AM 33.3% A+m2(t) 3 可见,正弦波做100%幅度调制时,调制效率仅为33.3%。 综上所述,AM信号的总功率包括载波功率和边带功率两部 分。只有边带功率才与调制信号有关。也就是说,载波分量 不携带信息,所以,调制效率低是AM调制的一个最大缺点。 《通信原理课件》
《通信原理课件》

5、调制信号为随机信号时已调信号的频谱特性 前面讨论了调制信号为确知信号时已调信号的频谱。在 一 般情况下,调制信号常常是随机信号,如语音信号。此 时,已调信号的频谱特性必须用功率谱密度来表示。 在通信系统中,我们所遇到的调制信号通常被认为是具 有各态历经性的宽平稳随机过程。这里假设(t)是均值为 零、具有各态历经性的平稳随机过程,其统计平均与时间 平均是相同的。由2.7节知,AM已调信号是一非平稳随机 过程,其功率谱密度为其自相关函数时间平均值的傅里叶 变换。 AM已调信号的自相关函数为 RAM(t,t+=E[SaM (t)SaM (t+] (3.2-9) 《通信原理课件》
《通信原理课件》

将(3.2-2)代入上式,并对其求时间平均 (cR(r)cos (3.2-10) 2 对式(3.2-10)进行傅里叶变换,可得已调信号的功率谱密 度为SDsB(o) Pw(a=风e-)+@+a】+a-a+(o+a】 (3.2-11) 2 上式中P(o)为调制信号的功率谱密度。 由功率谱密度可以求出已调信号的平均功率 Pw=∫Pr(odo-2+A (3.2-12) 其中 R=了ao-a)+aa+a】o-式 (3.2-13) 《通信原理课件》
《通信原理课件》

P(-0)+P.(+.o.(oM )(3.2-14) 比较式(3.2-13)和式(3.2-6)以及式(3.2-14)和式(3.2-7) 可见,在调制信号为确知信号和随机信号两种情况下,分别 求出的已调信号功率表达式是相同的。考虑到本章模拟通信 系统的抗噪声能力是由信号平均功率和噪声平均功率之比 (信噪比)来度量。因此,为了后面分析问题的简便,我们 均假设调制信号(基带信号)为确知信号。 《通信原理课件》
《通信原理课件》 2 1 1 1 [ ( ) ( )] ( ) 2 4 4 1 ( ) 2 P P P d P d m m c m c m m t − − = − + + = = (3.2-14) 比较式(3.2-13)和式(3.2-6)以及式(3.2-14)和式(3.2-7) 可见,在调制信号为确知信号和随机信号两种情况下,分别 求出的已调信号功率表达式是相同的。考虑到本章模拟通信 系统的抗噪声能力是由信号平均功率和噪声平均功率之比 (信噪比)来度量。因此,为了后面分析问题的简便,我们 均假设调制信号(基带信号)为确知信号
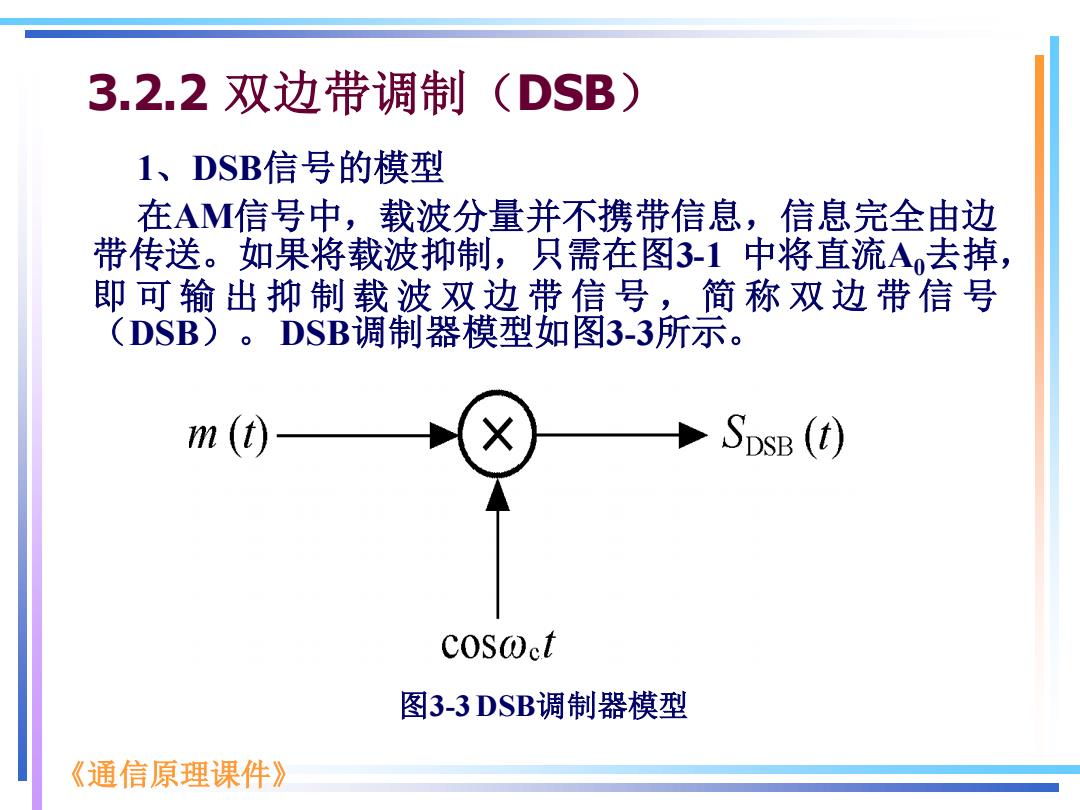
3.2.2双边带调制(DSB) 1、DSB信号的模型 在AM信号中,载波分量并不携带信息,信息完全由边 带传送。如果将载波抑制,只需在图3-1中将直流A去掉, 即可输出抑制载波双边带信号,简称双边带信号 (DSB)。DSB调制器模型如图3-3所示。 m (t) SDSB (t) coS@ct 图3-3DSB调制器模型 《通信原理课件》
《通信原理课件》 3.2.2 双边带调制(DSB) 1、DSB信号的模型 在AM信号中,载波分量并不携带信息,信息完全由边 带传送。如果将载波抑制,只需在图3-1 中将直流A0去掉, 即 可 输 出 抑 制 载 波 双 边 带 信 号 , 简 称 双 边 带 信 号 (DSB)。 DSB调制器模型如图3-3所示。 图3-3 DSB调制器模型