
2、AM信号的时域表达 由图3-1可得AM的时域表达式为 SaM (t)=[A+m(t)]cos(@t+) (3.2-2)》 为了分析问题的方便,令00,这样假设并不影响我们 讨论的一般性。 3、调制信号为确知信号时AM信号的频谱特性 虽然实际模拟基带信号(①是随机的,但我们还是从简单入 手,先考虑(①)是确知信号时AM信号的傅氏频谱,然后再分 析()是随机信号时调幅信号的功率谱密度。 由式(3.2-2)可知 San (t)=[A.+m(t)]cos @t =Ao cos @t+m(t)cos @t 《通信原理课件》
《通信原理课件》

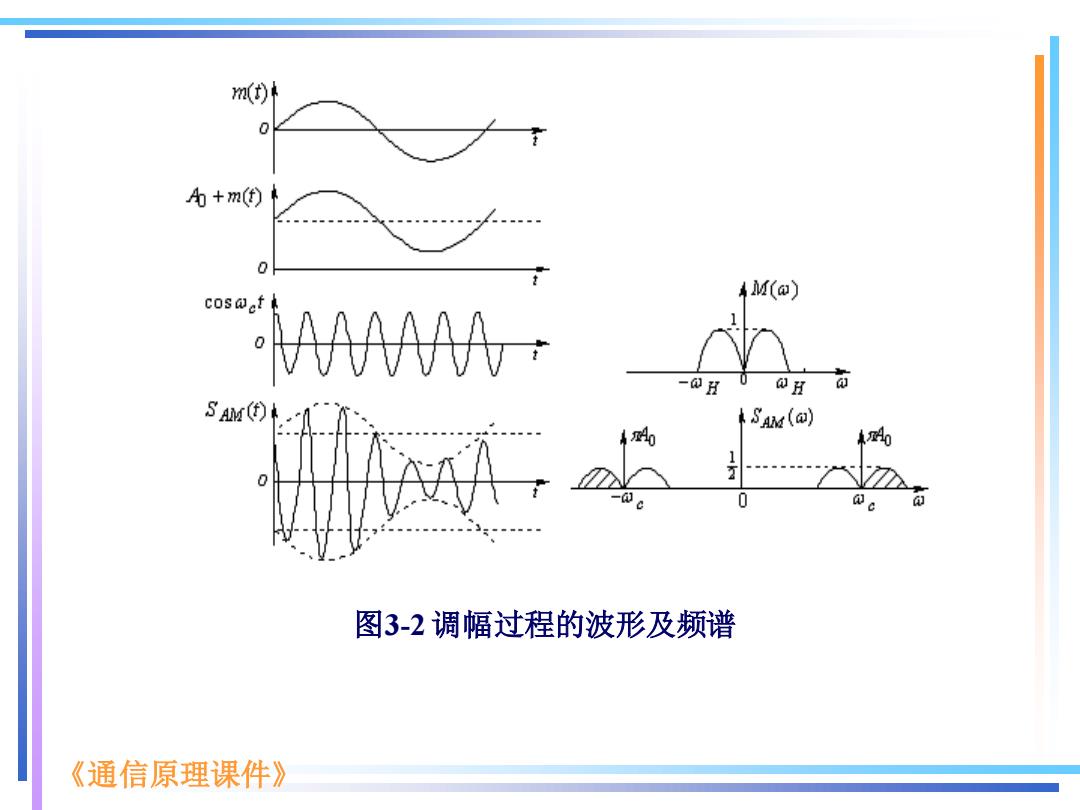
设m(①的频谱为M(w),由傅氏变换的理论可得已调信 号SAM()的频谱SAM(w)为 SAM(@)=6o-,)+60+,J+与M@-m)+Mω+】 (3.2-3) 图3-2所示为AM的波形和相应的频谱图 由图3-2可以看出,第一:AM波的频谱与基带信号的频谱呈 线性关系,只是将基带信号的频谱搬移到处,并没有产生新 的频率成分,因此AM调制属于线性调制;第二:AM信号波 形的包络与基带信号成正比,所以AM信号的解调既可采用 相干解调,也可采用非相干解调(包络检波)。第三:AM的 频谱中含有载频和上、下两个边带,无论是上边带还是下边 带,都含有原调制信号的完整信息,故已调波的带宽为原基 带信号带宽的两倍,即 BAM =2fH (3.2-4) 上式中,「为调制信号的最高频率。 《通信原理课件》
《通信原理课件》
m(t) 0 角+m(① 0 AM(@) MAAAA 一0H 0H S AM(f SAM(@) 0 c 图3-2调幅过程的波形及频谱 《通信原理课件》
《通信原理课件》 图3-2 调幅过程的波形及频谱

4、AM信号的功率分配与调制效率 幅度调制(AM)信号在1电阻上的平均功率应等于SA() 的均方值。当m()为确知信号时,SA()的均方值即为其平 方的时间平均,即 Pau sh (t) =[A,+m()]2c0s20.() (3.2-5) =A cos2@.t+m(t)cos'@1+2m(1)Ap cos'@t 前面已假设调制信号没有直流分量,即m⑩=0,而且()是 与载被无关的较为缓慢变化的信号。 所以 PAM= 6 .m20) 2 2 Pe+Pm 《通信原理课件》
《通信原理课件》

6 式中P。= 为不携带信息的载波功率 (3.2-6) 2 Pm m2(0 为携带信息的边带功率 (3.2-7) 2 可见,AM调幅波的平均功率由不携带信息的载波功率与 携带信息的边带功率两部分组成。所以涉及到调制效率的 概念。 定义边带功率Pm与PAM的比值为调制效率,记为?w。即 m2(t 1AM (3.2-8) PAM A6+m2(t) 显然,AM信号的调制效率总是小于1。 《通信原理课件》
《通信原理课件》