《电路》课程教学资源（课后课件）有例题_第13章 非正弦周期

Ikm锯齿波的振幅频谱图21元SDUNi1-元-?3元1T/24元-T/2000l 2030 401 50lQ邵资锯齿波的傅里叶级数展并为i(t) = 21cos(の;t-900)cos(2it+900) +2元1cos(30t-900)c0s(40,t+900) + ..3S外传！G今后若无说明，均指振幅频谱11

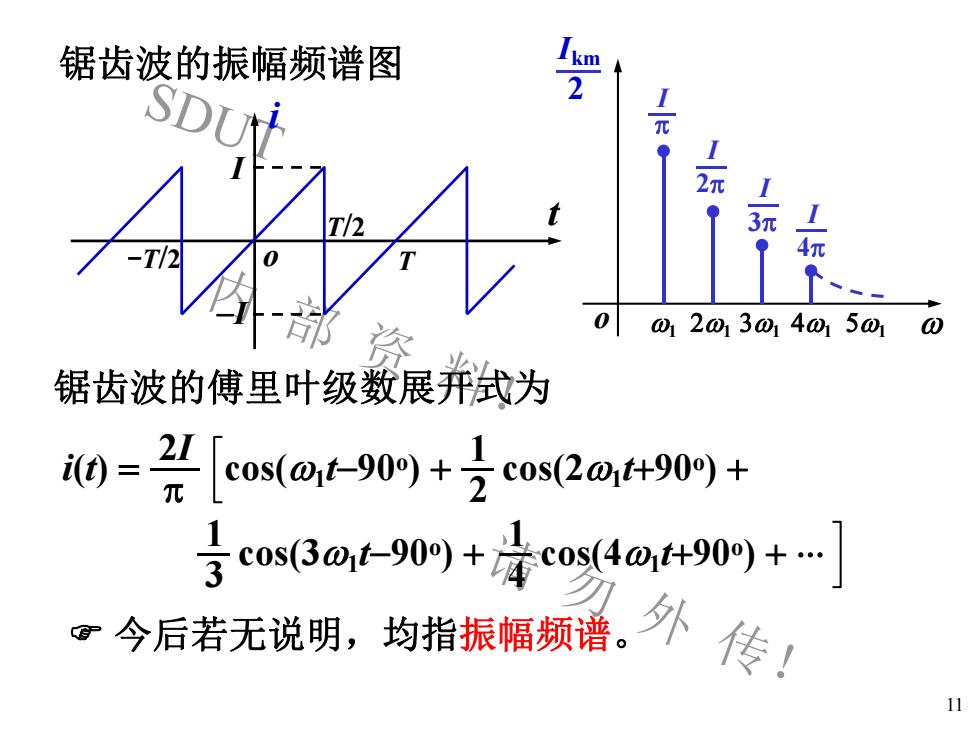
SDUT 内 部 资 料！ 请 勿 外 传！ 11 锯齿波的振幅频谱图  今后若无说明，均指振幅频谱。 i o t I-I T/2 -T/2 T i(t) = p 2I cos(1 t-90 o) + 2 1 cos(21 t+90 o) + 3 1 cos(31 t-90 o) + 4 1 cos(41 t+90 o) +  锯齿波的傅里叶级数展开式为 o 1 21 31 41 51  Ikm 2 I p I 2p I 3p I 4p

例：求下图方波的傅里叶级数展开式及频谱。UTti(t)T/21T内部资料！2元元ot请勿外传！12

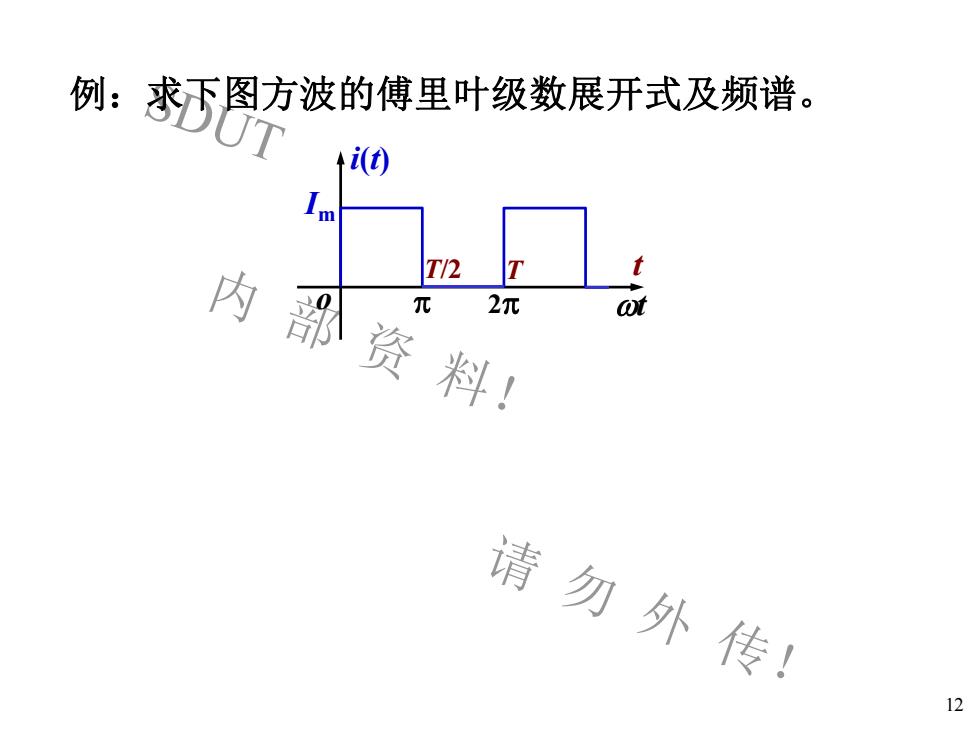
SDUT 内 部 资 料！ 请 勿 外 传！ 12 例：求下图方波的傅里叶级数展开式及频谱。 o t i(t) T/2 Im T p 2p t

例：求下图方波的傅里叶级数展开式及频谱SDUTi(t)0≤t<≤T/2m11T/2≤t≤ TtT/2T02元元ot部[a,cos(kot) + b,sin(koit)f(t) ao+解：(1)展开式T/210Imdt:直流分量：i(t)dtao=2T-2元1元cos(kan) d(an)=基波、讠谐波分量：ak=·元元Im cos(kot)d(ot)sin(kot)0元k元013

SDUT 内 部 资 料！ 请 勿 外 p 传！ 1 1 1 13 例：求下图方波的傅里叶级数展开式及频谱。 (1)展开式 i(t) = Im ， 0≤t ≤ T/2 0 ， T/2 ≤ t ≤ T o t i(t) T/2 Im T p 2p t a0 = T ∫0 i(t)dt T = T ∫ 0 Im dt T/2 = 2 Im 直流分量: 基波、谐波分量: f(t) = a0+∑[akcos(k1 t) + bksin(k1 t)] k=1 ∞ ak = ∫ 0 Im cos(kt)d(t) p = Im kp sin(kt) 0 p = 0 解: p ∫0 i(t)cos(kt) d(t)= 1 2p

ak =0a,=SDUT2元Ti(t) sin(kot) d(ot)Im sin(kot) d(ot)bk=元爪010内部、0k为偶数[1-cos(k元)]资21mk元k为奇数院8>代入 ,f(t)=ao+[axcos(kot) + bksin(kot)]k=121m得 i(t)sin5ot +...)sin3ot:sinot +-23元V卜传！14

SDUT 内 部 资 料！ 请 勿 外 传！ 14 bk = p ∫ 0 i(t) sin(kt) d(t) 2p 1 = p ∫0 Im sin(kt) d(t) p 1 = 0 k 为偶数 kp 2Im k 为奇数 = Im kp [1-cos(kp)] i(t) = 2 Im (sint + 3 1 + 2Im p sin3t + 5 1 sin5t +.) f(t) = a0+∑ [akcos(kt) + bksin(kt)] k=1 ∞ 代入 得 0 2 0 = ak = I a m

1m21m11(2)频谱sin5ot + ...sin3ot +i(t) :sinot +1523元 1m= 0aoa221m(k为奇数)21k元m(k为奇数)2Xk元Lbk-900相位d=areta资料！21mpk4相位频谱幅度频谱元1ko 30 50 701请131刃37-900ko传！?3000507015

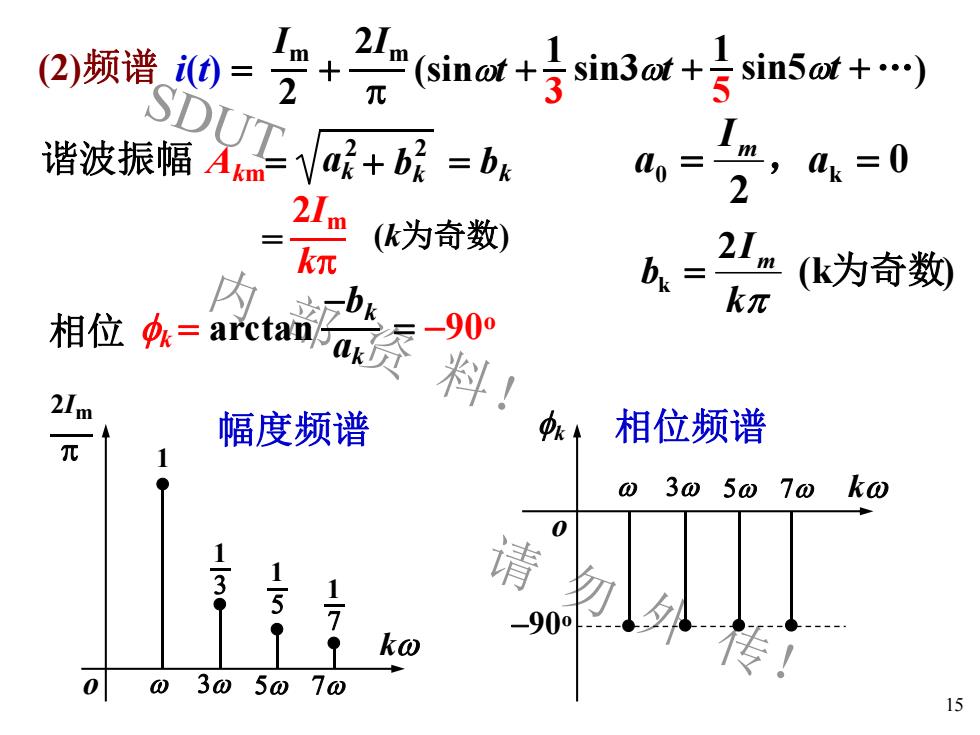
SDUT 内 部 资 料！ 请 勿 外 传！ 15 幅度频谱 相位频谱 1 3 2Im p o k  3 5 7 1 1 5 1 7 k o  3 5 7 k -90 o k = arctan ak -bk = -90 o Akm = ak 2 + bk 2 谐波振幅 = bk (2)频谱 0 2 0 = ak = I a m ， (k ) 2 k 为奇数 kp I b m kp = (k为奇数) 2Im = 相位 i(t) = 2 Im (sint + 3 1 + 2Im p sin3t + 5 1 sin5t +.)