《电路》课程教学资源（课后课件）有例题_第13章 非正弦周期

211m1分析sin5ot +...sin3ot -sSUTsinot-352元i(t)i(t)ot取到5次谐波的情况理论上，一个收敛的傅里叶级数要直流分量取无穷多项，才能准确代表原函数。基波分量三次谐波*实用中！根据展开式的收敛速度和误差要求敢前几项，高次谐五次谐波波可以忽略。16

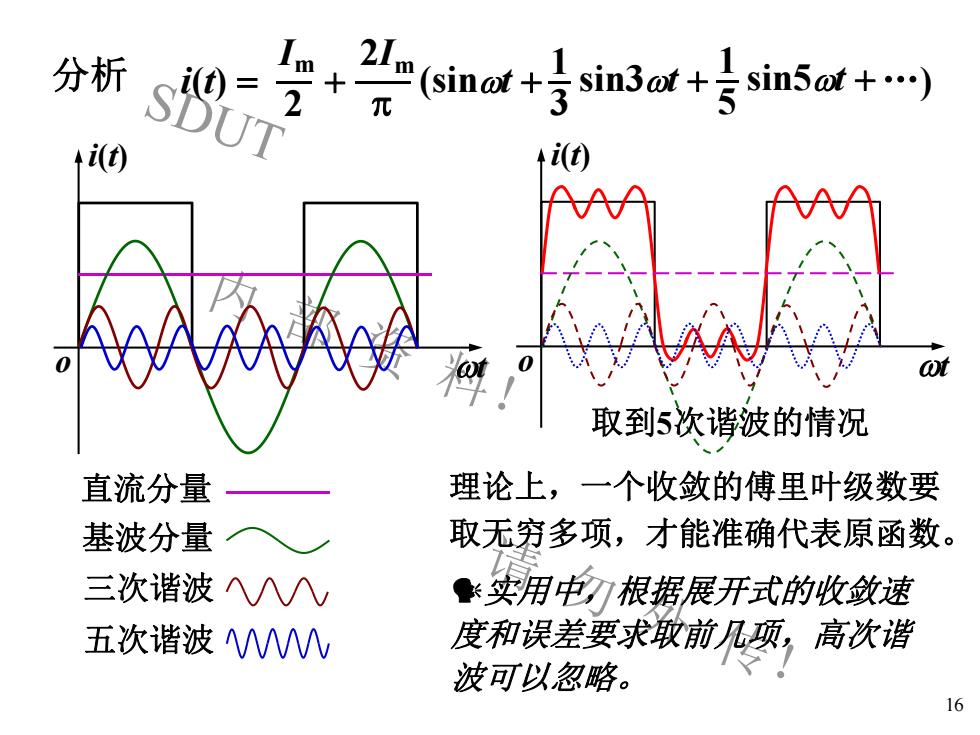
SDUT 内 部 资 料！ 请 勿 外 传！ 16 o t i(t) i(t) = 2 Im (sint + 3 1 + 2Im p sin3t + 5 1 sin5t +.) 基波分量 三次谐波 五次谐波 直流分量 o t i(t) 取到5次谐波的情况 实用中，根据展开式的收敛速 度和误差要求取前几项，高次谐 波可以忽略。 理论上，一个收敛的傅里叶级数要 取无穷多项，才能准确代表原函数。 分析

$13-3有效值、平均值和平均功率5回忆兰角函数的性质(k为整数,下同)①sin、cos在一个周期③正交性质(kq)内的积分为0;?2元coskot sinqot d(ot) =0?2元0roskh(a资！02元coskot cosqot d(ot) =0②sin2、cos2在一个周0期内的积分为元；2元sinkot sinqot d(ot) =0?2元请勿外传！cos2kot d(ot) = 元-17

SDUT 内 部 资 料！ 请 勿 外 传！ 17 §13-3 有效值、平均值和平均功率 ①sin、cos在一个周期 内的积分为0； 回忆三角函数的性质 ∫ 0 2p coskt d(t) = 0 ∫ 0 2p cos 2kt d(t) = p (k为整数,下同) ③正交性质 (k≠q) ∫0 2p coskt sinqt d(t) =0 ∫ 0 2p coskt cosqt d(t) =0 ∫ 0 2p sinkt sinqt d(t) =0 ②sin2 、cos 2 在一个周 期内的积分为p；

1.有效值周期量的有效值等于其瞬时值的方均根值，即SDUI8若 i(t)=l,+E Ikm cos(k)it +Φk)k=188i(t)2= I+21 Z Ikmcos(koit+Φk)+[ Z Ikmcos(koit+Φ)3k=1K则I=料！i(t)d08-/F),(1h+21,2/mcos(kol1+0-/2Z Ikmcos(ka,t+Φk)1)dtk=1k=1请上安报号中的积分安可以分糖求外，传！18

SDUT 内 部 资 料！ 请 勿 外 传！ 1 18 1.有效值 若 i(t) = I0 +S k=1 ∞ Ikm cos(k1 t +k) i(t) 2= I0 2+2I0S k=1 ∞ Ikmcos(k1 t+k)+[ k=1 S ∞ Ikmcos(k1 t+k)] 2 周期量的有效值等于其瞬时值的方均根值，即 则 I = T ∫ T i2(t)dt 0 T ∫ 0 T dt = 1 {I0 2+2I0S k=1 ∞ Ikmcos(k1 t+k)+[ k=1 S ∞ Ikmcos(k1 t+k)] 2} 上式根号中的积分式可以分解为：