
2.信息熵(Entropy) 预期能得到的平均信息量,I(P)的数学期望值。 对于M个灰阶:P;i=1,2,.,M M M 熵H=∑pI(p,)=-∑p,log2A 例1,当P;=1/4,i=1,2,3,4 H=2 当P1=1/2,P2=1/4,P3=P4=1/8 H=1.75 数字图像处要 ■■
2.信息熵(Entropy) 预期能得到的平均信息量,I(Pi )的数学期望值 。 对于M个灰阶: Pi i= 1,2,…., M = = = • = M i 1 M i 1 熵 H ( ) - log2 i p i i i p I p p 例1, 当Pi = 1/4 , i= 1,2,3,4 H = 2 当P1 = 1/2, P2 = 1/4, P3 = P4 = 1/8 H = 1.75
例2,二值图象,x:=0,1 0值概率:p 1值概率:1-p 1 H=plog2+(1-p)log20-) H 1 H~p变化关系可以发现, 当p=0.5时熵最大。 1.0 0.5 1 p 教字图像处要 ■■■■
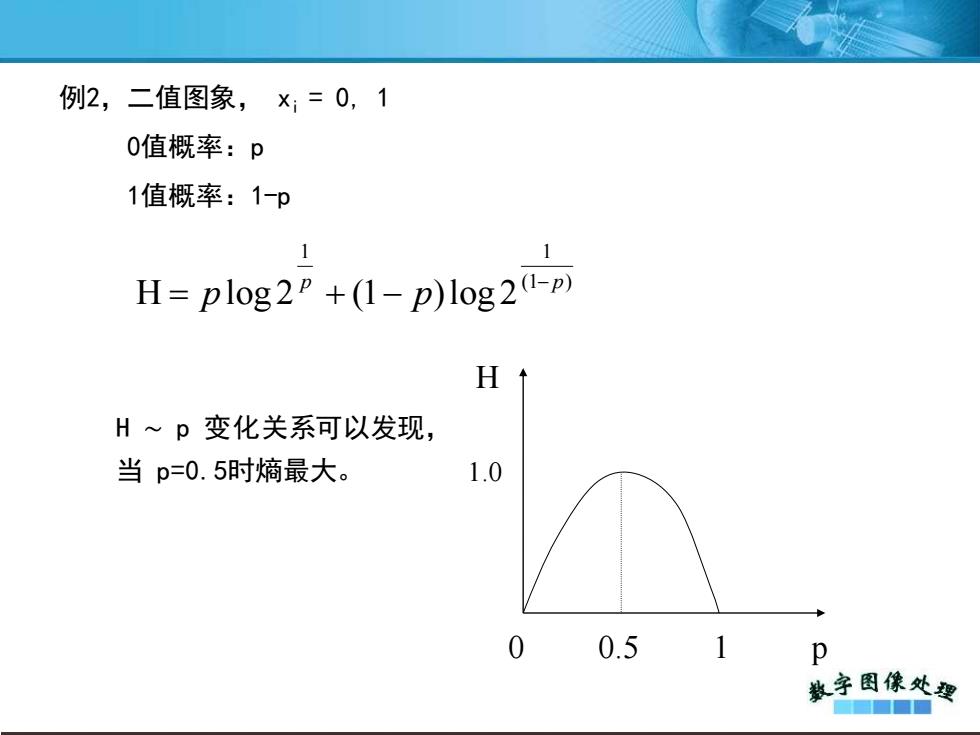
例2,二值图象, xi = 0, 1 0值概率:p 1值概率:1-p (1 ) 1 1 H log 2 (1 )log 2 p p p p − = + − H ∼ p 变化关系可以发现, 当 p=0.5时熵最大。 0 0.5 1 p H 1.0