
Social Choice Procedure 3: The Hare System At this stage we have lists that are at least one candidate shorter than that with which we started Now,we simply repeat the same process for the revised list. The procedure stops when either some candidate is on top of at least half of the (shortened)lists,or when all the remaining candidates occur at the top of exactly the same number of lists (in which case this set of candidates is declared to be the social choice set)
At this stage we have lists that are at least one candidate shorter than that with which we started. Now, we simply repeat the same process for the revised list. The procedure stops when either some candidate is on top of at least half of the (shortened) lists, or when all the remaining candidates occur at the top of exactly the same number of lists (in which case this set of candidates is declared to be the social choice set). Social Choice Procedure 3: The Hare System

students Choice 18 12 10 9 4 2 1st Choice A B C D E E 2nd Choice D E B C B 3rd Choice E D E E 4th Choice C C D B C B 5th Choice B A A A A A Since there are 55 students,at least 28 are needed for a majority. Notice that no candidate is on top of at least 28 of the lists,we therefore delete the candidate which is on top of the fewest lists. Delete Candidate E
A D E B C 10 A B E C D 9 A C D E B 12 2nd Choice D B C 3rd Choice E D D 4th Choice C C B 5th Choice B A A 1 A E E st Choice 18 4 2 students Choice Since there are 55 students, at least 28 are needed for a majority. Notice that no candidate is on top of at least 28 of the lists, we therefore delete the candidate which is on top of the fewest lists. Delete Candidate E !

students Choice 18 12 10 9 4 2 1st Choice A B C D B C 2nd Choice D D B C D D 3rd Choice C C D B B 4th Choice B A A A A A AB CD 1816128 Again no candidate is on top of at least 28 of the lists, we therefore delete the candidate which is on top of the fewest lists. Delete Candidate D
A D B C 10 A B C D 9 A C D B 12 2nd Choice D D D 3rd Choice C C B 4th Choice B A A 1st Choice A B C 18 4 2 students Choice Again no candidate is on top of at least 28 of the lists, we therefore delete the candidate which is on top of the fewest lists. Delete Candidate D ! A B C D 18 16 12 8
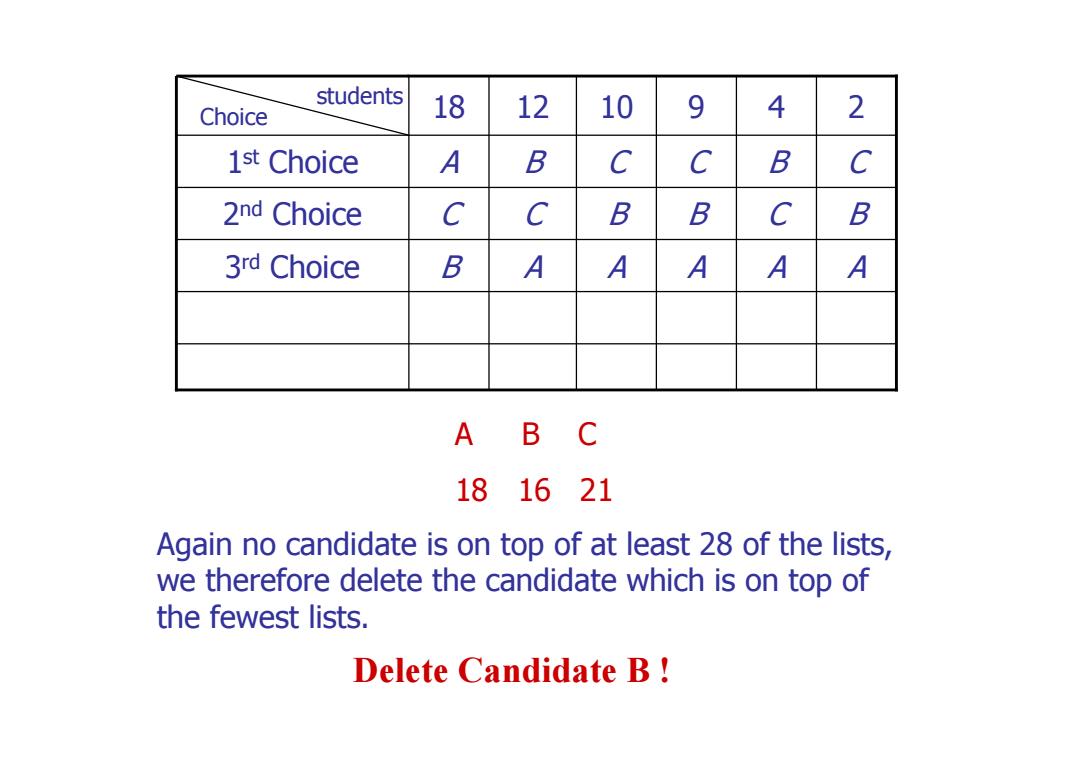
students Choice 18 12 10 9 4 2 1st Choice A B C C B C 2nd Choice C C B B C B 3rd Choice B A A A B C 181621 Again no candidate is on top of at least 28 of the lists, we therefore delete the candidate which is on top of the fewest lists. Delete Candidate B!
A B C 10 A B C 9 A C B 12 2nd Choice C C B 3rd Choice B A A 1st Choice A B C 18 4 2 students Choice Again no candidate is on top of at least 28 of the lists, we therefore delete the candidate which is on top of the fewest lists. Delete Candidate B ! A B C 18 16 21
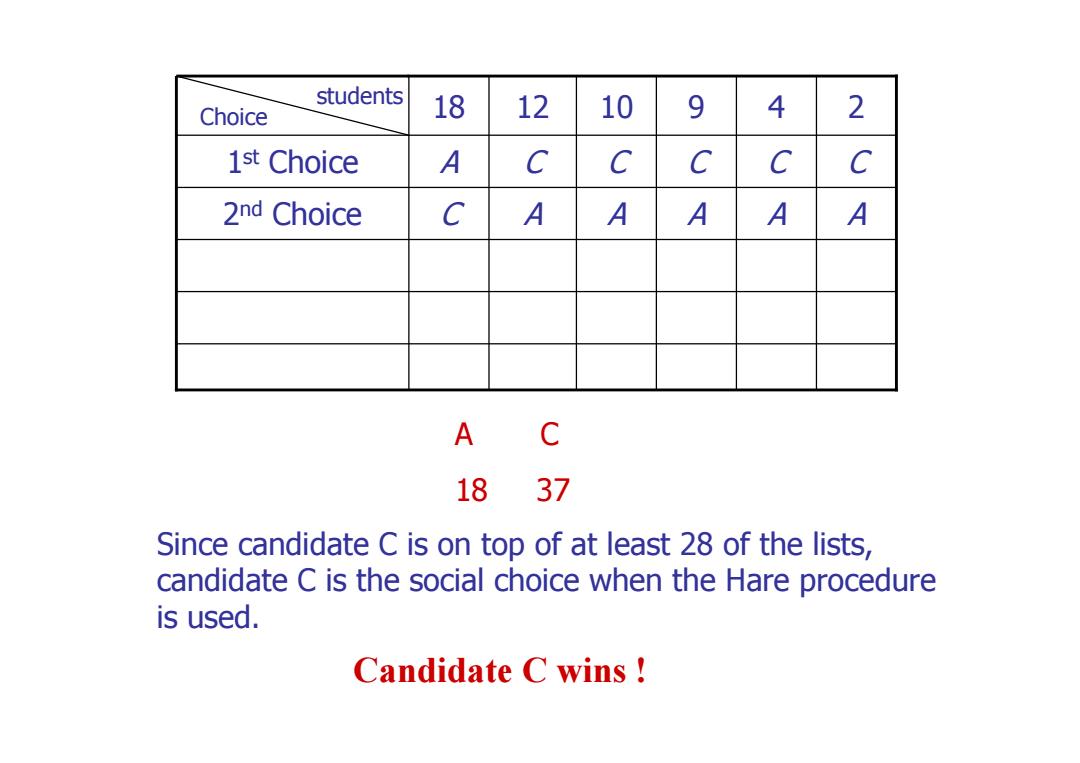
students Choice 18 12 10 9 4 2 1st Choice A C C C C 2nd Choice C AA AA A AC 1837 Since candidate C is on top of at least 28 of the lists, candidate C is the social choice when the Hare procedure is used. Candidate C wins
A C 10 A C 9 A C 12 2nd Choice C A A 1st Choice A C C 18 4 2 students Choice Since candidate C is on top of at least 28 of the lists, candidate C is the social choice when the Hare procedure is used. Candidate C wins ! A C 18 37