5.2一阶电路和二阶电路的频率响应 二、二阶电路 二阶带通举例 ◆H(Go 1/3 wo(jw) H(jw)=Ho wo 幅频的最大值发生在ω处 幅频特性 Ho H(jo)= ω,称为中心角频率。 1+Q 0_0g 00 π/2 相频特性o)=-arctan 000 G π/2
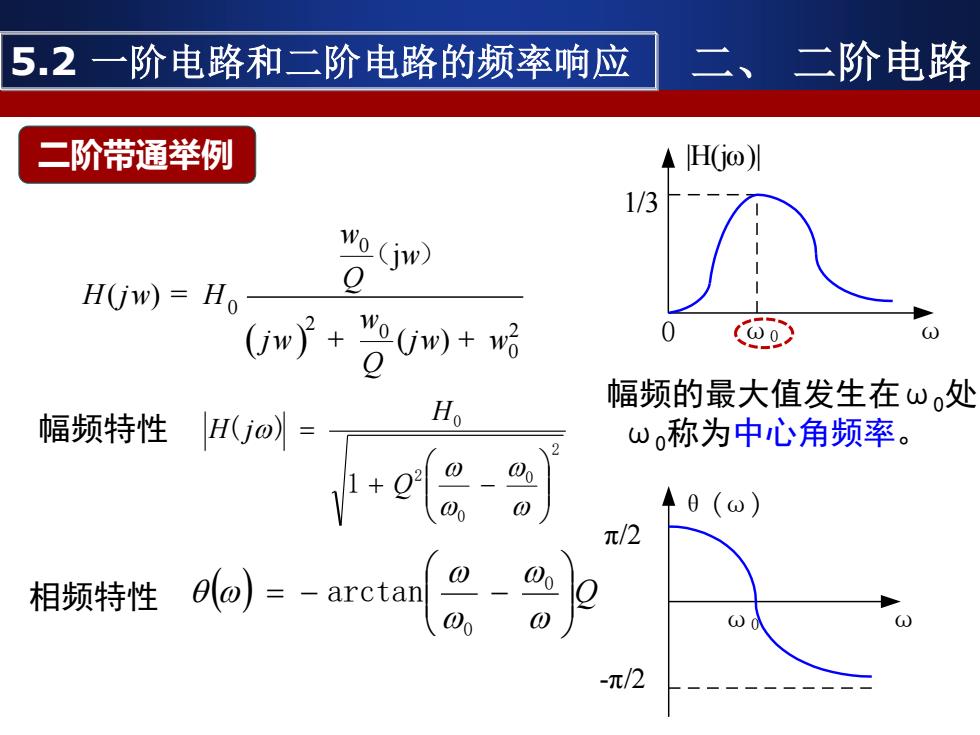
幅频特性 2 0 0 2 0 1 ( ) + − = Q H H j ω0 ω θ(ω) π/2 -π/2 5.2 一阶电路和二阶电路的频率响应 二、 二阶电路 ( ) Q = − − 0 0 相频特性 arctan 二阶带通举例 0 ω0 ω 1/3 |H(jω)| 幅频的最大值发生在ω0处, ω0称为中心角频率。 ( ) 0 0 2 0 2 0 j ( ) ( ) Q H j H j j Q w w w w w w w = + + ( )
5.2一阶电路和二阶电路的频率响应 二、二阶电路 当H(jω)|下降到其最大值的0.707倍时,对 ◆HGo)川 应的频率称为截止频率,用ωc1、 wc2表示。 1/3 H(jo) 1 1 H max 1+02 0c_ 00 @c 00c1000c2 G @C _- 1 +1 0c2= 00 20 20 00 20 20 通频带 ωc1w〈ωc2的频率范围为通带。通带的宽度称为带宽或通频带, 用B表示。 B=0C2-0C1= 00 (rad/s) 或B (H2)
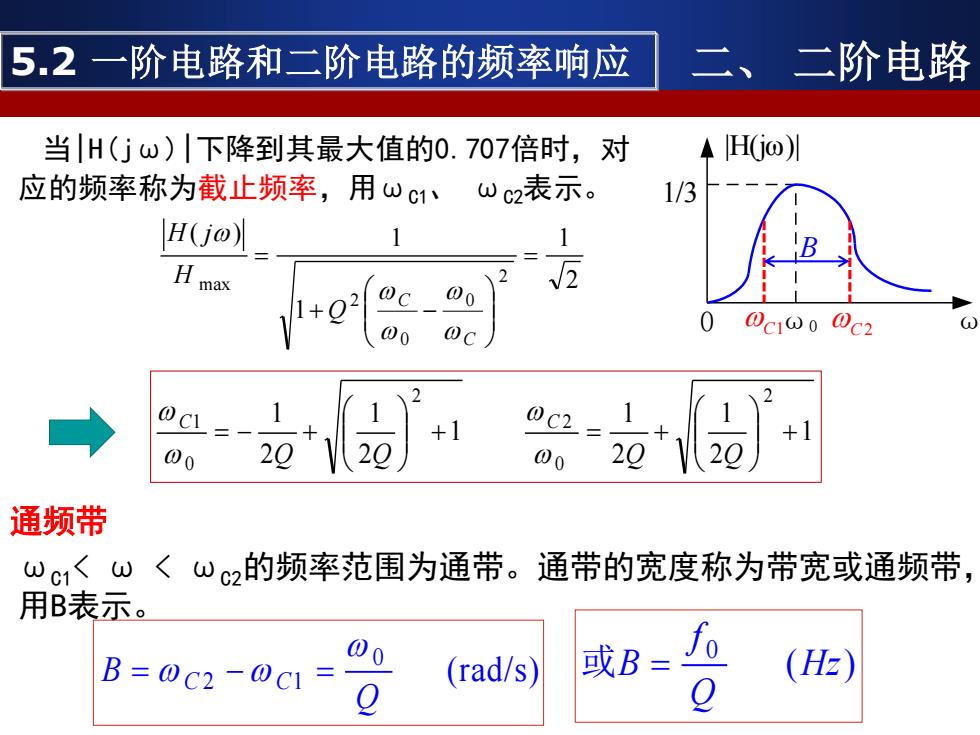
通频带 当|H(jω)|下降到其最大值的0.707倍时,对 应的频率称为截止频率,用ωC1、 ωC2表示。 2 1 1 ( ) 1 2 0 0 2 max = + − = C C Q H H j ωC1< ω < ωC2的频率范围为通带。通带的宽度称为带宽或通频带, 用B表示。 (rad/s) 0 2 1 Q B C C = − = ( ) 0 Hz Q f 或B = 5.2 一阶电路和二阶电路的频率响应 二、 二阶电路 0 ω0 ω 1/3 |H(jω)| C1 C2 B 1 2 1 2 1 1 2 1 2 1 2 0 2 2 0 1 + + = + = − + Q Q Q Q C C

5.2一阶电路和二阶电路的频率响应 二、二阶电路 二阶带阻举例 joC 3 joC 例3如图双T电路是一个带阻电路。若以U, 1 为激励,以U,2为响应,求电压比函 1/R 数H(j0)=U2/心1,并分析其频率特性。①心, 2/R0卡jo2C 节点法 节点2:(joC+1/R)02-joCU3-(1/R)04=0 节点3:(joC+j0C+2/R)U,-joCU,-joCU2=0 节点4:(Ujo2C+1/R+1VR)U4-(1/R)U1-(1/R)U,=0
例3 如图双T电路是一个带阻电路。若以 为激励,以 为响应,求电压比函 数 ,并分析其频率特性。 节点法 U1 +− U2 +− C R C 2CR R 2 U1 2 1 H j U U ( ) = U2 节点2: 节点3: 节点4: 2 3 4 ( 1 ) (1 ) 0 j C R U j CU R U + − − = 3 1 2 ( 2 ) 0 j C j C R U j CU j CU + + − − = U1 +− U2 +− j C 1 R j C j C 2 1 2 3 4 1 R 2 R 4 1 2 ( 2 1 1 ) (1 ) (1 ) 0 j C R R U R U R U + + − − = 5.2 一阶电路和二阶电路的频率响应 二、 二阶电路 二阶带阻举例