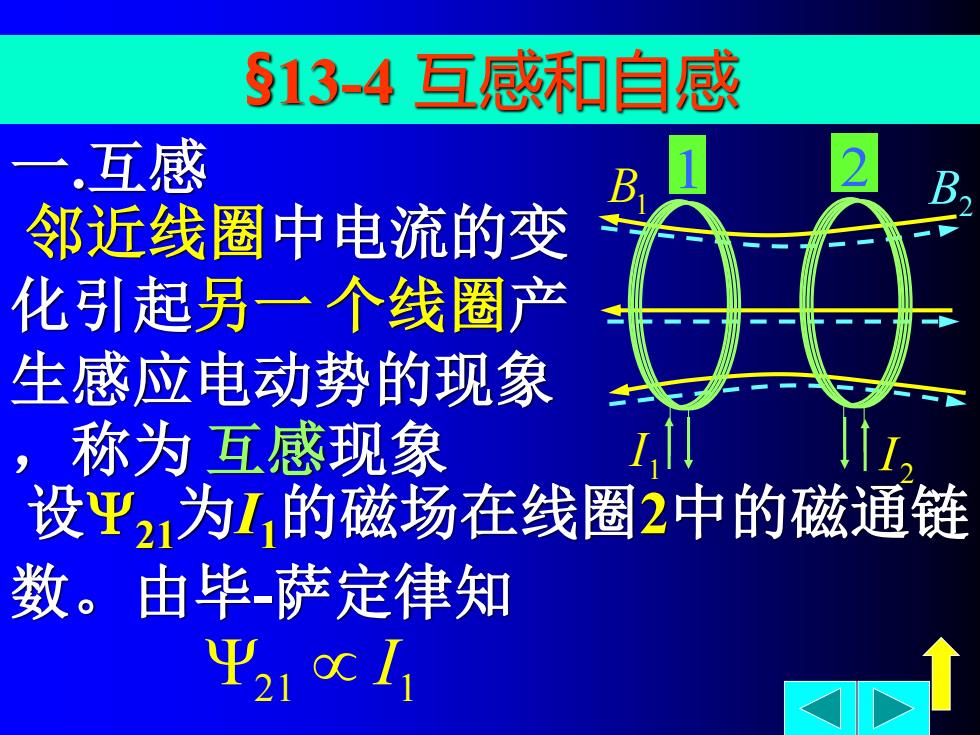
§13-4互感和自感 一互感 邻近线圈中电流的变 化引起另一个线圈产 生感应电动势的现象 称为互感现象 设Ψ21为1,的磁场在线圈2中的磁通链 数。由毕萨定律知 Ψ21
一 .互感 邻近线圈中电流的变 化引起另一 个线圈产 生感应电动势的现象 ,称为 互感现象 B1 B2 1 I 2 I 1 2 §13-4 互感和自感 设21为I1的磁场在线圈2中的磁通链 数。由毕-萨定律知 21 1 I

Y2 =M2I, M21: 线圈1对线圈2的互感系数 当I变化时,线圈2中的互感电动势 2= Y2-M2 dt 同理 €1= Y2=-M2 dt d M12: 线圈2对线圈1的互感系数
21 21 1 = M I M21:线圈1对线圈2的互感系数 当I1变化时,线圈2中的互感电动势 dt d 2 1 2 = − dt dI M 1 = − 2 1 同理 dt d 1 2 1 = − dt dI M 2 = − 1 2 M12:线圈2对线圈1的互感系数

可证M21=M2=M M:两回路间的互感系数,简称互感 单位:亨利H 说明 M与线圈的几何形状、匝数、相对 位置以及周围磁介质的磁导率有关 M的大小反映出两线圈间相互产生 感应电动势的能力
可证 M21 = M12= M M:两回路间的互感系数,简称互感 说明 :M与线圈的几何形状、匝数、相对 位置以及周围磁介质的磁导率有关 单位:亨利(H) M的大小反映出两线圈间相互产生 感应电动势的能力

[例⑧]半径为R的长直磁介质棒上,分 别绕有长为lN匝)和l,N,匝)的两个 螺线管.口由此特例证明M12=M21=M; 当螺线管1中的电流变化率为d亚/dt时 ,求螺线管2中的互感电动势 解:设螺线管1中通有电流I, ∴.B=un1
[例8]半径为R的长直磁介质棒上,分 别绕有长为l1 (N1匝)和l2 (N2匝)的两个 螺线管. 由此特例证明M12 =M21 =M; 当螺线管1中的电流变化率为dI1 /dt时 ,求螺线管2中的互感电动势 1 l 2 l 解: 设螺线管1中通有电流I1 1 1 1 B = n I 1 1 1 I l N =

通过螺线管2的磁通链数为 P21=NBS= LN N27R2I Z 又设螺线管2中通有电流I2,则 B2=Wn212=W
通过螺线管2的磁通链数为 21 = N2 B1 S 1 1 2 1 2 l N N R I = 1 2 1 2 1 I M = 1 2 1 2 l N N R = = n1 n2 V2 又设螺线管2中通有电流I2,则 2 2 2 B = n I 2 2 2 I l N =