
第十三章电磁感应 §13-1电磁感应的基本定律 一、电磁感应现象 当穿过一个闭合导体回路所包围的面积内的磁通量发生变化时,在导体回路中就会 产生电流,这种现象称为电磁感应现象(1831年)。 二、楞次定律(1833年) (纯电阻)闭合回路中产生的感应电流具有确定的方向,它总是使感应电流所产生 的通过回路面积的磁通量,去补偿或反抗引起感应电流的磁通量的变化。 或:感应电流的效果总是反抗引起感应电流的原因。 这里:“效果”可以理解为感应电流激发的磁场,也可以理解为因感应电流出现而引起 的机械作用。“原因”既可以指磁通量的变化,也可指引起磁通量变化的相对运动或回 路的形变。 ▲实质:感应电流取楞次定律所述的方向,是能量守恒和转化定律的必然结果。 例题:楞次定律是能量守恒所必需的。换句话说,如果电磁感应的规律正好与楞次定律 相反,则能量守恒定律不成立。试用简单例子加以说明。 三、法拉第电磁感应定律 导体回路中感应电动势£,的大小与穿过回路的磁通量的变化率心成正比。 d dt 或e=-K dt 对于国际单位制: K=1 dΦ 8,=- (适用于单匝导线组成的回路)
第十三章 电磁感应 §13-1 电磁感应的基本定律 一、电磁感应现象 当穿过一个闭合导体回路所包围的面积内的磁通量发生变化时,在导体回路中就会 产生电流,这种现象称为电磁感应现象(1831 年)。 二、楞次定律(1833 年) (纯电阻)闭合回路中产生的感应电流具有确定的方向,它总是使感应电流所产生 的通过回路面积的磁通量,去补偿或反抗引起感应电流的磁通量的变化。 或:感应电流的效果总是反抗引起感应电流的原因。 这里:“效果”可以理解为感应电流激发的磁场,也可以理解为因感应电流出现而引起 的机械作用。“原因”既可以指磁通量的变化,也可指引起磁通量变化的相对运动或回 路的形变。 ▲ 实质:感应电流取楞次定律所述的方向,是能量守恒和转化定律的必然结果。 例题:楞次定律是能量守恒所必需的。换句话说,如果电磁感应的规律正好与楞次定律 相反,则能量守恒定律不成立。试用简单例子加以说明。 三、法拉第电磁感应定律 导体回路中感应电动势 i 的大小与穿过回路的磁通量的变化率 d dt 成正比。 i dΦ ε dt 或 i dΦ ε dt = −K 对于国际单位制: K=1 i dΦ ε dt = − (适用于单匝导线组成的回路)

对于多匝线圈串联,每匝的磁通分别为中,中2,“,中 dt dt dt =-m+0,+.0,) 平=④,+中,++Φ、叫做磁通匝链数或全磁通。 若中,相同,均为中,则平=N中 dt ▲感应电动势的方向问题: 规定: 【,回路的正方向→确定ε的正负 2、曲面法线的正方向→确定Φ的正方向方可满足法拉第定律 3、与的关系满足右手法则 如果闭合电路的电阻为R, 当1=1o,中=中;1=4,Φ=中,通过回路中任一截面的感应电量(迁移的电量) ★q=1h=-元=最o。-o,) 例题: 如图,环形螺线管n=5000匝/米, 安=-20安培秒,截面S=2x10米,在环上 再绕一线圈A,N=5匝,R=2.0欧姆 求:1、A中6,及1, 2、2秒内通过A的电量q 解:环内的B≈4l,通过A的D=S
对于多匝线圈串联,每匝的磁通分别为 1 2 , , , N 1 2 N i d d d dt dt dt = − − − − 1 2 ( ) N d dt d dt = − + + = − = + + + 1 2 N 叫做磁通匝链数或全磁通。 若 i 相同,均为 ,则 = N , i d dΦ ε dt dt N = − = − ▲ 感应电动势的方向问题: 规定: 方可满足法拉第定律 与 的关系满足右手法则 曲面法线 的正方向 确定 的正方向 回路 → → 3、 L n 2、 n 1 的正方向 确定 的正负 、 L 如果闭合电路的电阻为 R, 1 i d I R dt = − 当 0 0 1 1 t t t t = = = = , ; , ,通过回路中任一截面的感应电量(迁移的电量) ★ 1 1 0 0 0 1 1 1 ( ) t i t q I dt d R R = = − = − 例题: 如 图 , 环 形 螺 线 管 n=5000 匝 / 米 , 20 / dI dt = − 安培 秒 ,截面 3 2 S 2 10− = 米 。在环上 再绕一线圈 A,N=5 匝, R=2.0 欧姆 求:1、A 中 i 及 i I 2、2 秒内通过 A 的电量 q 解:环内的 B nI 0 ,通过 A 的 0 = nIS

5-小水盟4s图-126r伏特 1=126×10=6.30×10安培 2 9=∫1,dh=6.30x10×2.0=126x103库仑 §13-2在磁场中运动的导线内感应电动势(动性电动势) 一、动生电动势 D=B.S=BII' 59品)=m →8,=Bw方向可由楞次定律得 到(从b指向a) 二、对动生电动势的解释 由金属电子理论: ∫F.=9×B=-ep×B F,=gE=-eE [F.=evB→向下 E=eE→向上 当eE=eBE=B,这时,。-y=El,即因 洛仑兹力作用的结果 6,=E=B与前面结果完全一致。 ▲以上说法与洛仑兹力不作功是否相矛盾呢?不矛盾。以下说明: 总洛仑兹力为:F=-(位+)×B,它与合成速度下+n垂直,不做功 然而分力,于=-(下×B)对电子做正功,形成动生电动势。而另一分力,F=-(下+)×B, 它沿-下方向,做负功。可以证明两功代数和为零,证明如下: F(下+)=0总功率为零
3 0 1.26 10 i d dI N nNS dt dt − = = = 伏特 3 1.26 10 4 6.30 10 2 i I − − = = 安培 2 1 4 3 6.30 10 2.0 1.26 10 t i t q I dt − − = = = 库仑 §13-2 在磁场中运动的导线内感应电动势(动生电动势) 一、动生电动势 = = B S Bll dl v dt = ( ) i d d dl Bll Bl dt dt dt = = = = i Blv 方向可由楞次定律得 到(从 b 指向 a) 二、对动生电动势的解释 由金属电子理论: m e F qv B ev B F qE eE = = − = = − m e F evB F eE = → = → 向下 向上 当 eE evB E vB = = , ,这时, a b v v El − = ,即因 洛仑兹力作用的结果 i = = El lvB 与前面结果完全一致。 ▲ 以上说法与洛仑兹力不作功是否相矛盾呢?不矛盾。以下说明: 总洛仑兹力为: F e v u B = − + ( ) ,它与合成速度 v u + 垂直,不做功。 然而分力, f e v B = − ( ) 对电子做正功,形成动生电动势。而另一分力, F e v u B = − + ( ) , 它沿 −v 方向,做负功。可以证明两功代数和为零,证明如下: F v u + = ( ) 0 总功率为零

F=了+ 代入上式并展开,子下+子+子+子.=0 因为子下=0,”.i=0 fn+了p=0或fi=-立 因此,洛仑兹力作用并不提供能量,而只是传递能量。 补充:导体在恒定磁场中运动时,动生电动势: ab=[(xB).dl 6>0,则。<4,:6b<0,则u,>4。 或s=∮,(×B)dl 例题:已知铜棒长L,在匀强磁场B中沿逆 时针方向绕轴以角速度旋转 1、 求铜棒中感生电动势的大小和方向 2、若是半径为L的铜盘绕圆心旋转,求中 心与边缘之间的电势差 解:1、在距0为1处取dl小段,速度v=ol ds,=-Bvdl=-Boldl (下×B)方向为从A->0 各小段的ds,的指向都是一样的, ∴e=-Bol=-BaL 5,的指向是从A到0的 :.Uo-U=BoL 另解:计算铜棒在单位时间所切割的磁感应线数来计算动生电动势 设△r内转过△0角度, AΦ=B.1L-LA8=1B 2、若是铜盘,可以看成是无数根并联的铜棒组成,结果同上。 例题:[程守诛普通物理学第四版p220.14 31如图, 1 )质量为M,长度为1的金属 棒b从静止开始沿倾斜的绝缘框架下滑,设磁场B竖直向上,求棒内的动生时势与时 间的函数关系,忽略摩擦。(2)如果金属棒b是沿光滑的金属框架下滑,结果有何不
F f f = + 代入上式并展开, f v f u f v f u + + + = 0 因为 f v f u = = 0, 0 f u f v + = 0 或 f u f v = − 因此,洛仑兹力作用并不提供能量,而只是传递能量。 补充:导体在恒定磁场中运动时,动生电动势: ( ) b ab a = v B dl 0, ab b u 则ua ; 0, ab b u 则ua 或 ( ) L = v B dl 例题:已知铜棒长 L,在匀强磁场 B 中沿逆 时针方向绕轴以角速度 旋转。 1、求铜棒中感生电动势的大小和方向 2、若是半径为 L 的铜盘绕圆心旋转,求中 心与边缘之间的电势差 解:1、在距 O 为 l 处取 dl 小段,速度 v =l , d Bvdl B ldl i = − = − , (v B) 方向为从 A->O 各小段的 d i 的指向都是一样的, 2 0 2 1 B ldl B L l i = − = − i 的指向是从 A 到 O 的 2 2 1 UO −U A = BL 另解:计算铜棒在单位时间所切割的磁感应线数来计算动生电动势。 设 t 内转过 角度, 2 2 1 2 1 = B L L = BL 2、若是铜盘,可以看成是无数根并联的铜棒组成,结果同上。 例题:[程守洙 普通物理学第四版 p220.14-13]如图,(1)质量为 M,长度为 l 的金属 棒 ab 从静止开始沿倾斜的绝缘框架下滑,设磁场 B 竖直向上,求棒内的动生时势与时 间的函数关系,忽略摩擦。(2)如果金属棒 ab 是沿光滑的金属框架下滑,结果有何不
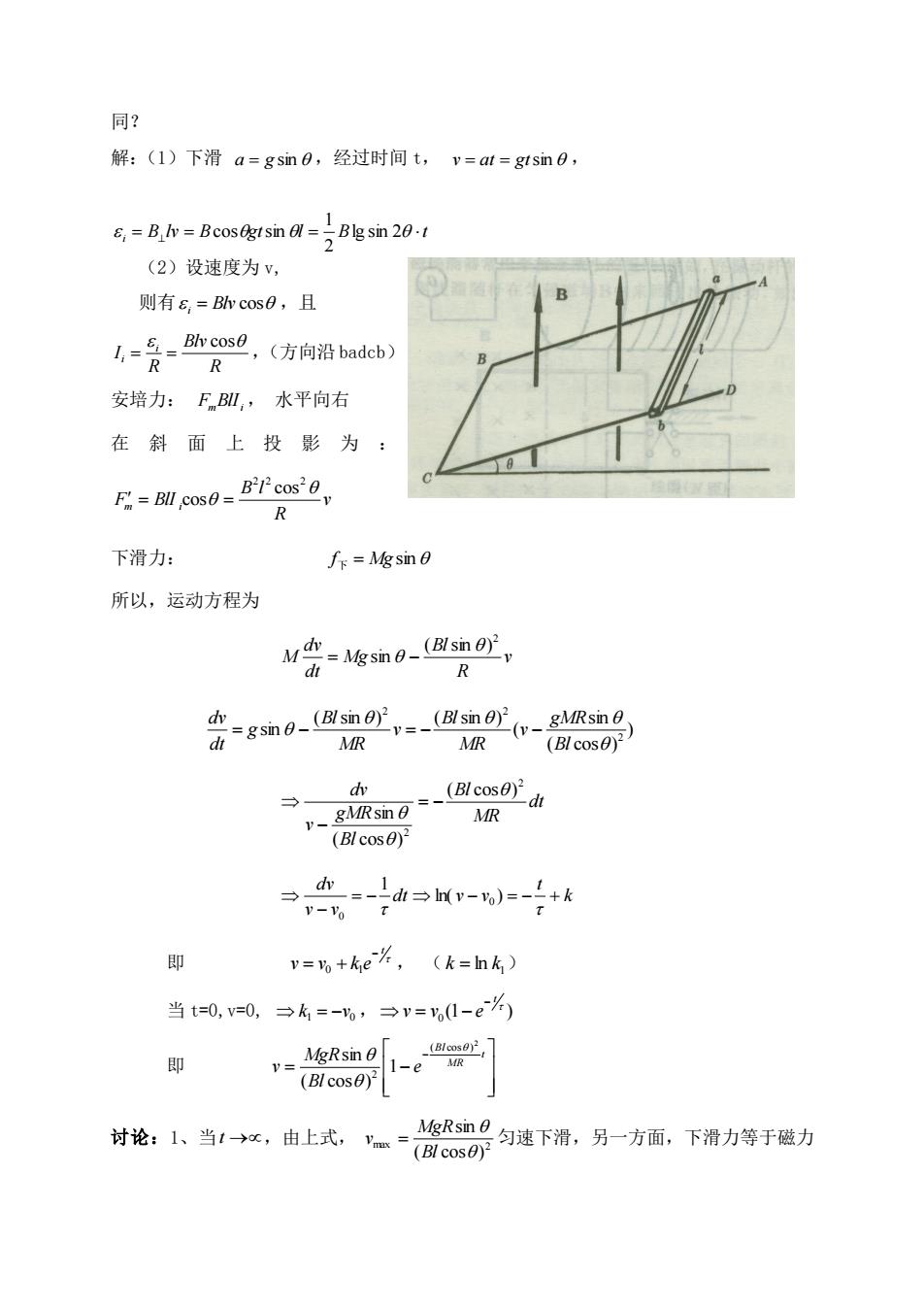
同? 解:(1)下滑a=gsin0,经过时间t,v=at=gtsin0 Bcosrn (2)设速度为v, 则有G,=B弥cos8,且 -是-卧9,(方向沿b) R 安培力:FB即,水平向右 在斜面上投影为: B c0s0 cos 0 R 下滑力: f:=Mgsin 0 所以,运动方程为 M密峻s如0圆阳, R -(v gMRsin MR MR (Bl cos0) (c 小 R v=肠+ke片,(k=nk) 当t=0,=0,→k=-,→v=w1-e%) 即 MgRsin 0 v=(Bicos0) 1-e R 时论:1、当,由上式一匀下滑,另一方,下滑力等于装力
同? 解:(1)下滑 a = g sin ,经过时间 t, v = at = gtsin , B lv B gt l B t i = = = ⊥ lg sin 2 2 1 cos sin (2)设速度为 v, 则有 i = Blv cos ,且 R Blv R I i i cos = = ,(方向沿 badcb) 安培力: FmBlIi , 水平向右 在 斜 面 上 投 影 为 : v R B l F BlI m i 2 2 2 cos = cos = 下滑力: f下 = Mg sin 所以,运动方程为 v R Bl Mg dt dv M 2 ( sin ) sin = − ) ( cos ) sin ( ( sin ) ( sin ) sin 2 2 2 Bl gMR v MR Bl v MR Bl g dt dv = − = − − dt MR Bl Bl gMR v dv 2 2 ( cos ) ( cos ) sin = − − k t dt v v v v dv = − − = − + − ln( ) 1 0 0 即 t v v k e − = 0 + 1 , ( 1 k = ln k ) 当 t=0,v=0, 1 0 k = −v , (1 ) 0 t v v e − = − 即 = − − t MR Bl e Bl MgR v 2 ( cos ) 2 1 ( cos ) sin 讨论:1、当 t → ,由上式, max 2 ( cos ) sin Bl MgR v = 匀速下滑,另一方面,下滑力等于磁力