电子科技大学：《贝叶斯学习与随机矩阵及在无线通信中的应用 BI-RM-AWC》课程教学资源（课件讲稿）06 Non-asymptotic Analysis for Large Random Matrix

6.1 Non-asymptotic Analysis:Concentration inequality Taking logarithms on both sides of equation,yields log,[ec]-log20s E[C]slogee where inequality (a)is derived via Jensens inequality. For logee,we can get unm含 12

12 Taking logarithms on both sides of equation, yields 6.1 Non-asymptotic Analysis: Concentration inequality   ( ) 2 2 2 log log log a C C     e C e −        where inequality (a) is derived via Jensens inequality. For , we can get 2 log C   e   ( ) ( ) 2 † 2 2 0 ! log log det log ! r i n t C r t i t t n n n e n n i i =                  = + =           −   I HH 

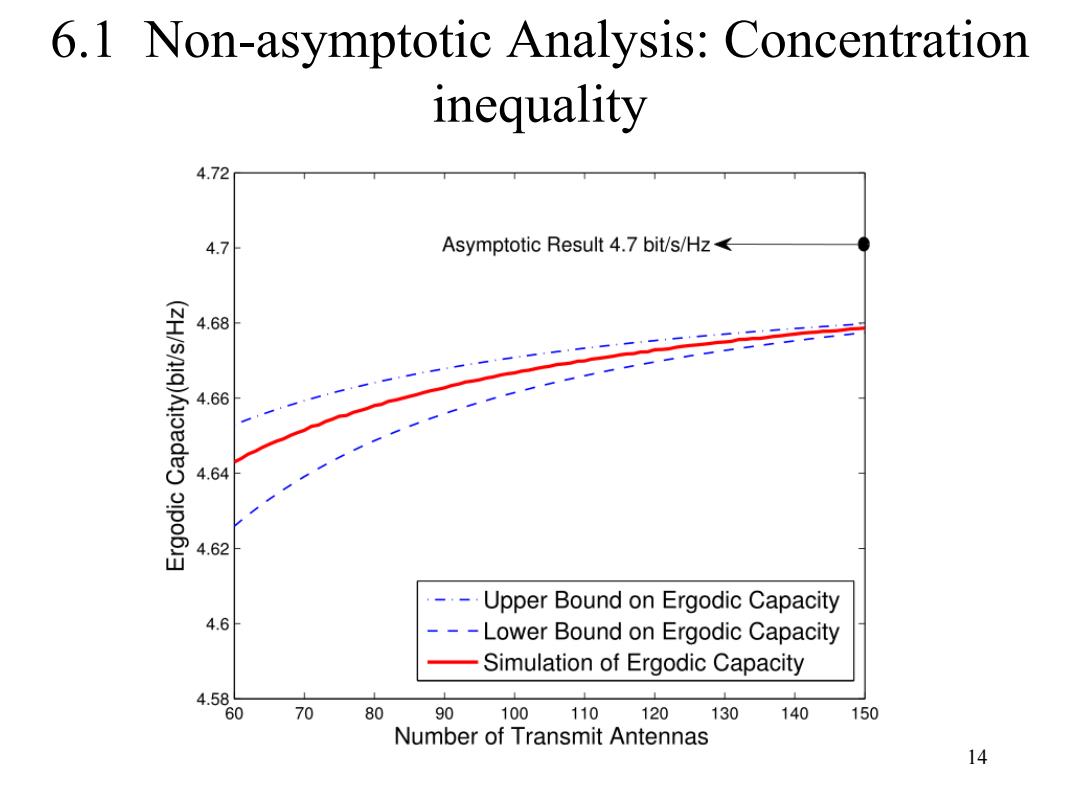
6.1 Non-asymptotic Analysis:Concentration inequality Hence,the upper and lower bounds on ergodic capacity is derived log2 T1g0s©sg:之7}2 We can see that he gap between the upper and lower bounds on ergodic capacity is log20.As the number of transmit antennas n, increases,the upper and lower bounds on ergodic capacity become tighter.If n,goes to infinity,the gap log2=0. 13

13 Hence, the upper and lower bounds on ergodic capacity is derived 6.1 Non-asymptotic Analysis: Concentration inequality ( ) ( )   ( ) ( ) 2 2 2 0 0 ! ! log log log ! ! r r i i n n t t r r t t i i t t n n n n C i i n i n i = =                       −        − −   We can see that he gap between the upper and lower bounds on ergodic capacity is log2ω. As the number of transmit antennas nt increases, the upper and lower bounds on ergodic capacity become tighter. If nt goes to infinity, the gap log2ω = 0

6.1 Non-asymptotic Analysis:Concentration inequality 4.72 4.7 Asymptotic Result 4.7 bit/s/Hz< 4.68 4.66 4.64 4.62 -Upper Bound on Ergodic Capacity 4.6 --Lower Bound on Ergodic Capacity -Simulation of Ergodic Capacity 4.5 60 70 80 90 100 110 120 130 140 150 Number of Transmit Antennas 14

14 6.1 Non-asymptotic Analysis: Concentration inequality

6.1 Non-asymptotic Analysis:Concentration inequality Moreover,concentration inequality of MIMO capacity can be written as tn, pC-B[C]>s2e 20t p{[C]-t<C<[C]+}≥2e2d kpPL Furthermore,replace t with we can get the instantaneous satisfies n qgc<0g 2L o1-2sn[“g】 15

15 6.1 Non-asymptotic Analysis: Concentration inequality Moreover, concentration inequality of MIMO capacity can be written as           2 2 2 2 2 2 2 2 t t t n L t n L p C C t e p C t C C t e −  −  −   −   +  Furthermore, replace t with , we can get the instantaneous satisfies 1/2 1/4 t k L n      1/2 1/2 1/4 1/4 t t k L k L C C C n n   −   + with probability at least 2 1/2 1 2exp 2 t   k n − −   

6.1 Non-asymptotic Analysis:Concentration inequality However,in massive MIMO,due to the large number of antennas, it is very hard to obtain ergodic capacity.But,we can use the bounds on the ergodic capacity to derive the statistical bounds for the instantaneous capacity,i.e.the instantaneous satisfies ko" 1og2 o 1.og,o5C's tog,) 1/4 1/4 n, wth probability at least 16

16 6.1 Non-asymptotic Analysis: Concentration inequality However, in massive MIMO, due to the large number of antennas, it is very hard to obtain ergodic capacity. But, we can use the bounds on the ergodic capacity to derive the statistical bounds for the instantaneous capacity, i.e. the instantaneous satisfies ( ) ( ) ( ) ( ) 1/2 1/2 2 2 2 1/4 1/4 0 0 ! ! log log log ! ! r r i i n n t t r r t t i i t t t t n n n n k L k L C = = i i n i n n i n                         − −    +     − −   with probability at least 2 1/2 1 2exp 2 t   k n − −   