
6.1 Non-asymptotic Analysis:Concentration inequality For convenience,we define the probability that the instantaneous capacity falls within the bounds as falling-in probability.From the bounds on instantsaneous capacity,we can observe that: 1).the falling-in probability will increase as the number of transmit antennas n,increase; 2).the bounds on instantaneous capacity will converge to ergodic capacity as the number of transmit antennas n,increase.Therefore, we can conclude that,as the number of transmit antennas n, increases,the randomness of instantaneous capacity gradually vanishes. 17
17 For convenience, we define the probability that the instantaneous capacity falls within the bounds as falling-in probability. From the bounds on instantsaneous capacity, we can observe that: 1). the falling-in probability will increase as the number of transmit antennas nt increase; 2). the bounds on instantaneous capacity will converge to ergodic capacity as the number of transmit antennas nt increase. Therefore, we can conclude that, as the number of transmit antennas nt increases, the randomness of instantaneous capacity gradually vanishes. 6.1 Non-asymptotic Analysis: Concentration inequality
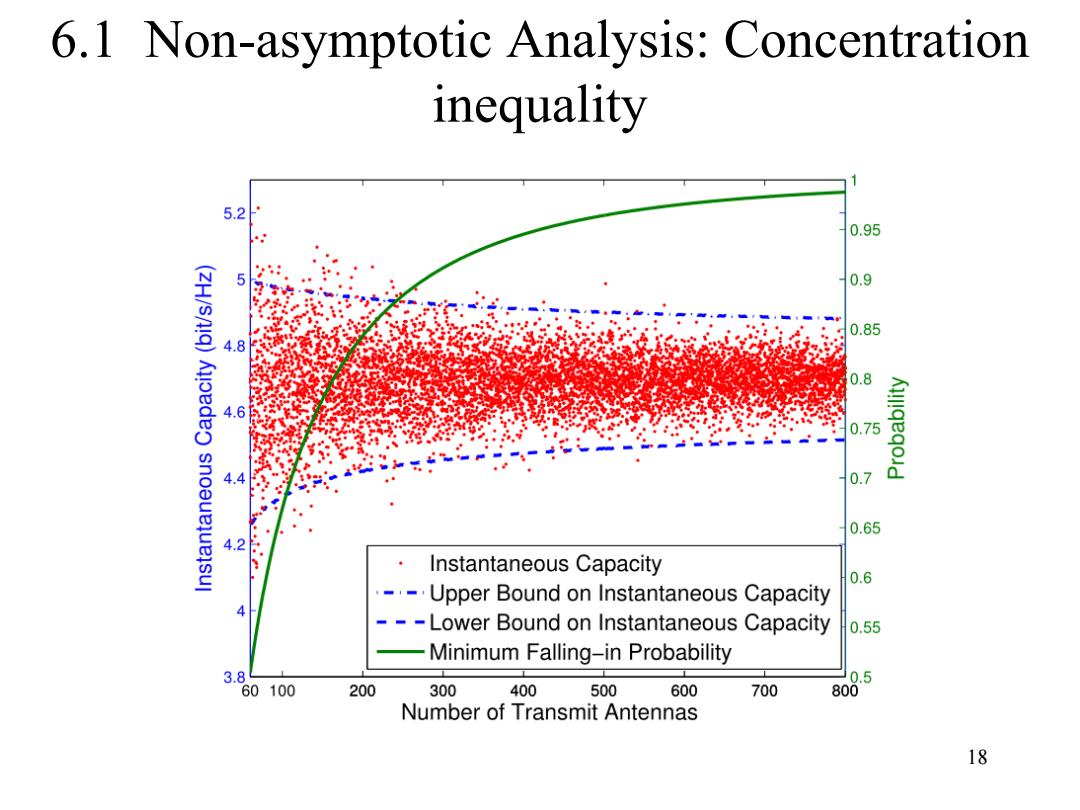
6.1 Non-asymptotic Analysis:Concentration inequality 5.2 0.95 0.9 0.85 0.75 0.7 0.65 2 Instantaneous Capacity 0.6 -Upper Bound on Instantaneous Capacity --Lower Bound on Instantaneous Capacity 0.55 Minimum Falling-in Probability 3. 0.5 60 100 200 300 400 500 600 700 80 Number of Transmit Antennas 18
18 6.1 Non-asymptotic Analysis: Concentration inequality