
多项式类的运动规律 一般形式 S=c+c1p+C2p2+c303+Λ+Cnp” 从动件的运动规律 v=0(C,+2c2p+3c30+A+ncnp"-) a=@(2c2 +6c0++n(n-I)c,p") 16
一般形式 多项式类的运动规律 从 = + + + + + n n 3 3 2 0 1 2 s c c ϕ c ϕ c ϕ Λ c ϕ 从 动件 的 从 = + + + + − ( ) 2 2 n 1 n 2 1 2 3 0 1 2 3 n v ω c 2c ϕ 3c ϕ nc ϕ ϕ ϕ ϕ ϕ Λ 的 运 动 的 = + + + − − ( ( ) ) n 2 2 3 n 2 a ω 2c 6c ϕ Λ n n 1 c ϕ 动 规律 16
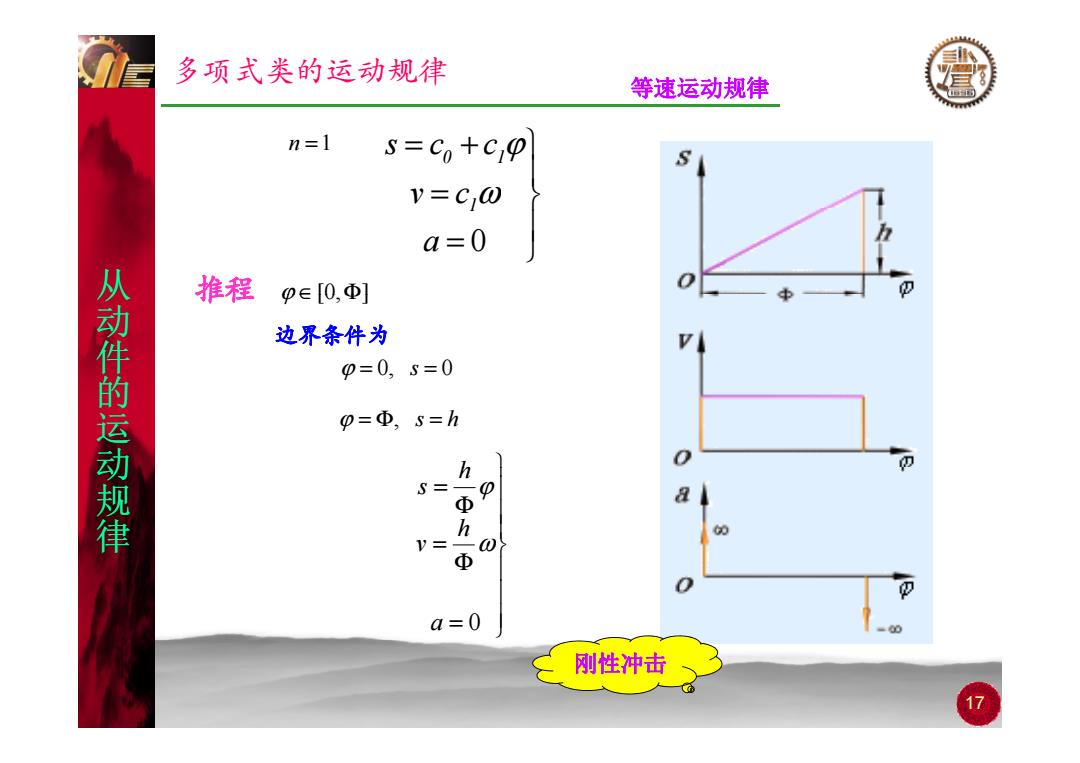
多项式类的运动规律 等速运动规律 n=1 s=Co+cp V=C,0 a=0 推程 pe[0,Φ] 从动件的运动规律 边界条件为 p=0,5=0 p=Φ,s=h h S Φ h Φ a=0 =00 刚性冲击 17
多项式类的运动规律 等速运动规律 = = + v c s c c 1 0 1 ω n = 1 ϕ 从 推程 ϕ ∈[0 Φ] a = 0 1 从 动件 的 从 推程 ϕ ∈[0,Φ] 边界条件为 的 ϕ = 0, s = 0 运 动 的 h ϕ = Φ, s = h 动 规律 Φ = Φ = h v h s ω ϕ = Φ a 0 17 刚性冲击
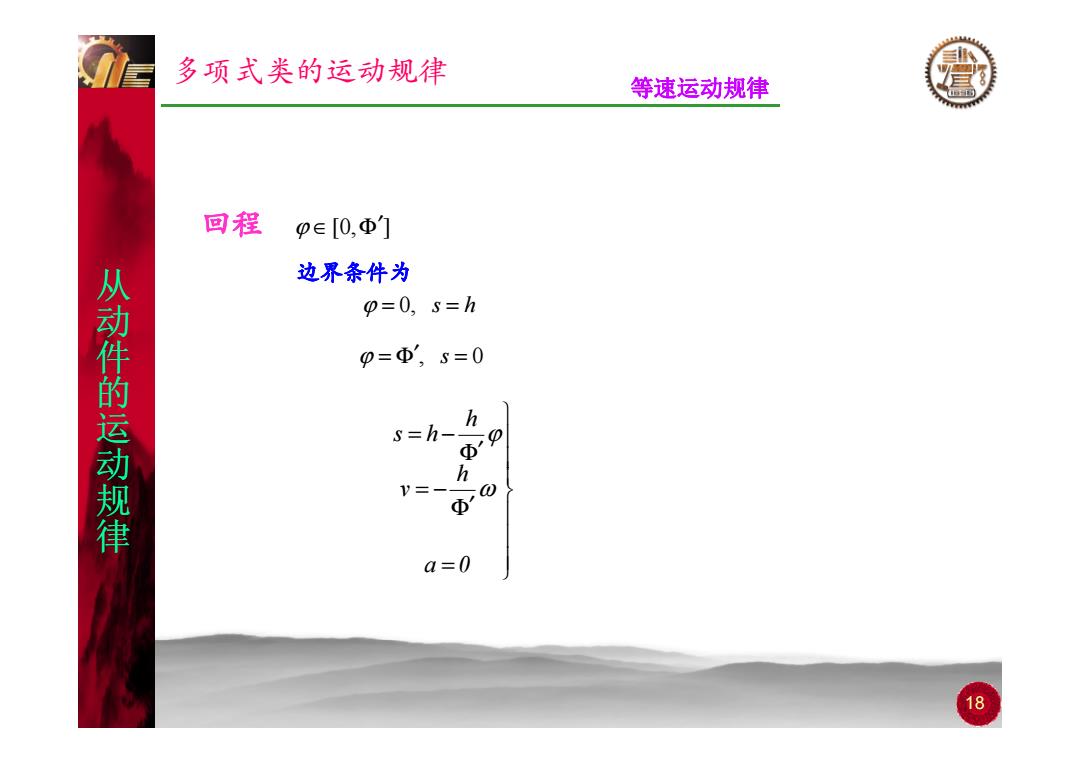
多项式类的运动规律 等速运动规律 回程 p∈[0,Φ] 边界条件为 =0,s=h 从动件的运动规律 p=Φ,s=0 h s=h h =0 18
多项式类的运动规律 等速运动规律 回程 ϕ ∈[0,Φ′] 从 边界条件为ϕ = 0, s = h ϕ = Φ′, s = 0 从 动件 的 从 Φ′ = −hh s h ϕ 的运 动 的 Φ′ = − h v ω 动 规律 a = 0 18
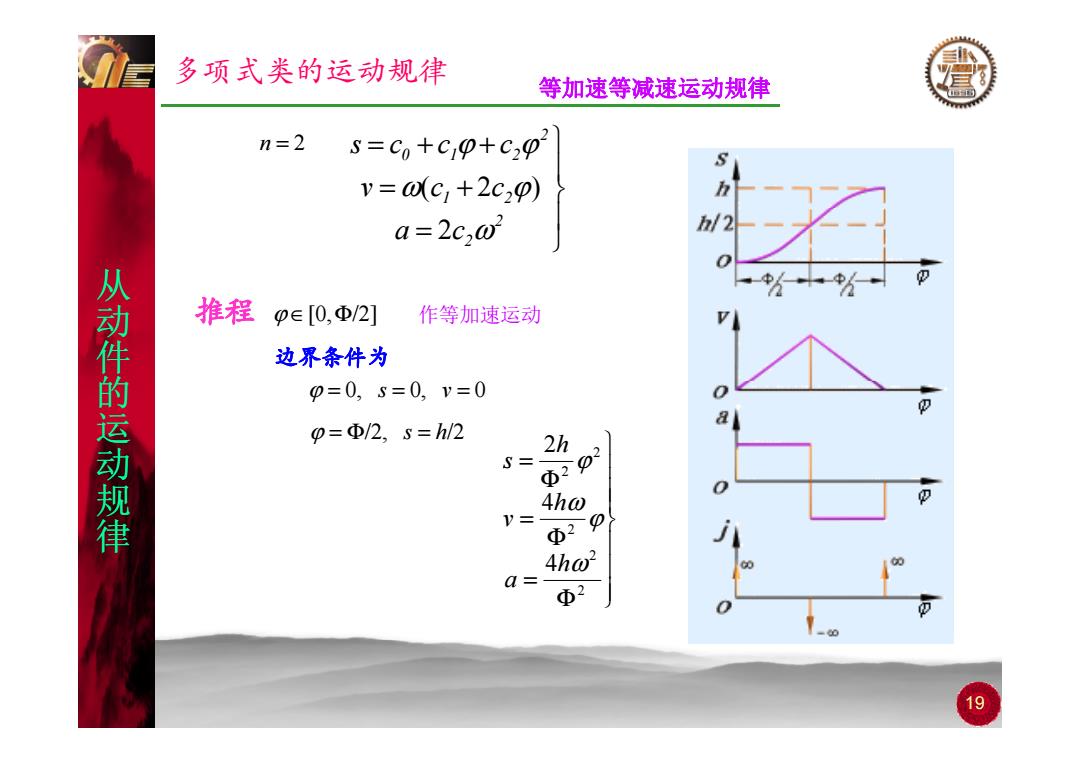
多项式类的运动规律 等加速等减速运动规律 n=2 S=Co+cp+c2 v=(C1+2C2p) a=2c2@ h/2 推程 p∈[0,Φ/2] 作等加速运动 从动件的运动规律 边界条件为 p=0,5=0,v=0 p=Φ/2,s=hl/2 2h S 4h@ V= Φ2 0 4ho2 Q= Φ2 19
多项式类的运动规律 等加速等减速运动规律 n = 2 = + = + + 1 2 2 0 1 2 v c c s c c c ω ϕ ϕ ϕ ( 2 ) 从 推程 = 2 2 a 2 c ω 从 动件 的 从 推程 ϕ ∈[0,Φ/2] 边界条件为 作等加速运动 的 运 动 的 ϕ = 0, s = 0, v = 0 ϕ = Φ/2, s = h/2 = 2 2 2 ϕ h s 动 规律 Φ = Φ 2 2 2 4 ϕ ω ϕ h h v s Φ = 2 2 4 h ω a 19

多项式类的运动规律 等加速等减速运动规律 n=2 S=co+co+c v=(C1+2C2p) a=2c,@ h/2 p∈[Φ/2,Φ] 作等减速运动 从动件的运动规律 边界条件为 p=Φ/2,s=hl/2,v=2h/Φ p=Φ,s=h,v=0 2h s=h- Φ2 Φ-p)2 4h@ 1= Φ2 (Φ-p) 4h02 Q= Φ2 柔性冲击 20
多项式类的运动规律 等加速等减速运动规律 n = 2 = + = + + 1 2 2 0 1 2 v c c s c c c ω ϕ ϕ ϕ ( 2 ) 从 ϕ ∈[Φ/2 Φ] 作等减速运动 = 2 2 a 2 c ω 从 动件 的 从 ϕ ∈[Φ/2, Φ] 边界条件为 ϕ = Φ/2, s = h/2, v = 2 h ω/ Φ 作等减速运动 的 运 动 的 ϕ = Φ, s = h, v = 0 2 h 动 规律 Φ − Φ = Φ − Φ = − 2 2 2 ( ) 4 ( ) 2 ϕ ω ϕ h v h s h Φ = − Φ 2 2 2 4 ( ) ω ϕ h a 20 柔性冲击