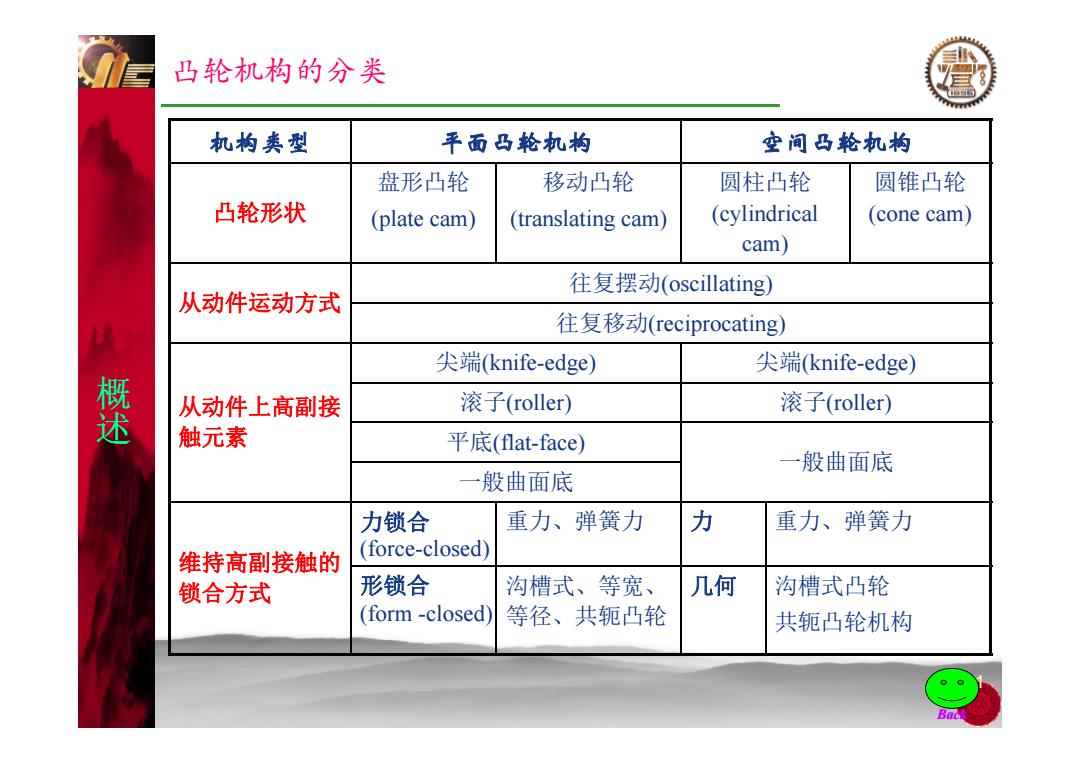
凸轮机构的分类 机构类型 平面马轮机构 空间马轮机构 盘形凸轮 移动凸轮 圆柱凸轮 圆锥凸轮 凸轮形状 (plate cam) (translating cam) (cylindrical (cone cam) cam) 往复摆动(oscillating) 从动件运动方式 往复移动(reciprocating) 尖端(knife-edge) 尖端(knife-edge) 槩 从动件上高副接 滚子(roller) 滚子(roller) 触元素 平底(flat-face) 一般曲面底 一 般曲面底 力锁合 重力、弹簧力 力 重力、弹簧力 维持高副接触的 (force-closed) 锁合方式 形锁合 沟槽式、等宽、 几何 沟槽式凸轮 (form-closed) 等径、共轭凸轮 共轭凸轮机构 Bac
凸轮机构的分类 机构类型 平面凸轮机构 空间凸轮机构 凸轮形状 盘形凸轮 移动凸轮 圆柱凸轮 ( li d i l 圆锥凸轮 凸轮形状 ( ) (plate cam) (translating cam) (cylindrical cam) (cone cam) 从动件运动方式 往复摆动(oscillating) 概 从动件运动方式 ( g) 往复移动(reciprocating) 概 尖端(knife-edge) 尖端(knife-edge) 述 从动件上高副接 触元素 滚子(roller) 滚子(roller) 平底(flat-face) 一般曲面底 一般曲面底 维持高副接触的 力锁合 (force-closed) 重力、弹簧力 力 重力、弹簧力 维持高副接触的 锁合方式 (force closed) 形锁合 (form -closed) 沟槽式、等宽、 等径、共轭凸轮 几何 沟槽式凸轮 共轭凸轮机构 11 Back
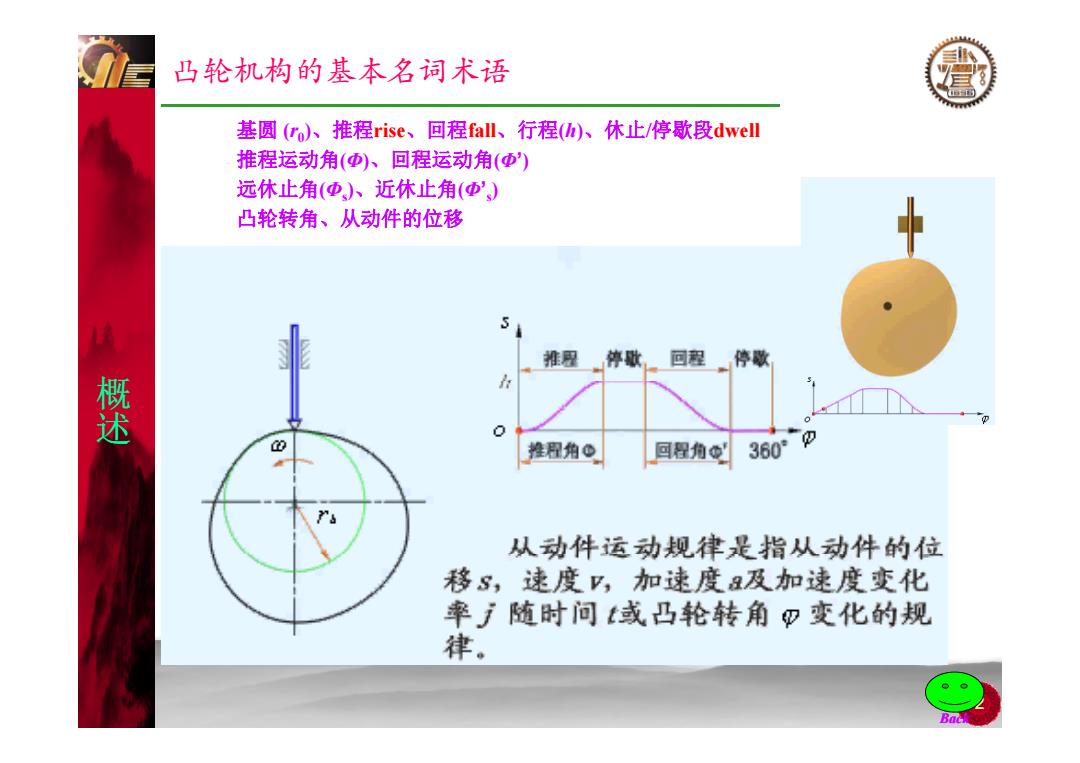
凸轮机构的基本名词术语 基圆(r)、推程rise、回程fall、行程()、休止/停歇段dwel 推程运动角()、回程运动角(Φ) 远休止角(Φ,)、近休止角(Φ) 凸轮转角、从动件的位移 推 回程停数 蟋 推程角© 回程角 360° 从动件运动规律是指从动件的位 移s,速度口,加速度a及加速度变化 率随时间或凸轮转角四变化的规 律。 Bac
凸轮机构的基本名词术语 基圆 ( r 0 )、推程rise、回程fall、行程 ( h )、休止/停歇段dwell 推程运动角 ( Φ )、回程运动角 ( Φ’) 远休止角 ( Φs)、近休止角 ( Φ’s) 凸轮转角、从动件的位移 概 述 12 Back
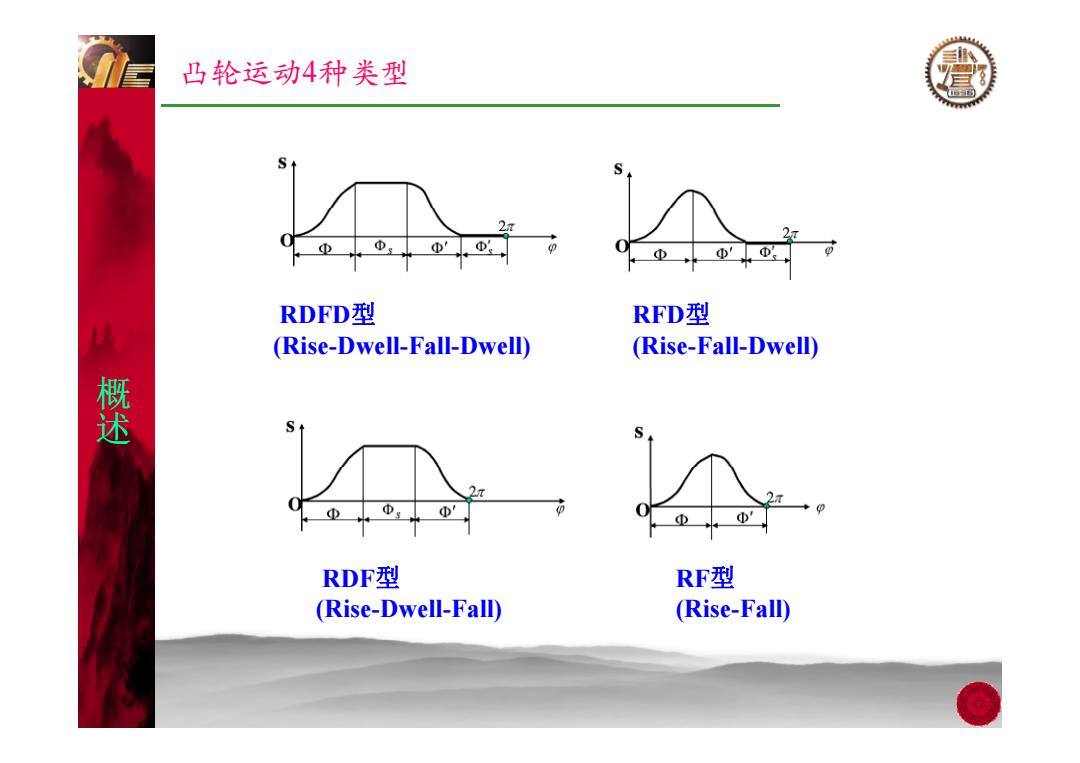
凸轮运动4种类型 2 Φ'Φ RDFD型 RFD型 (Rise-Dwell-Fall-Dwell) (Rise-Fall-Dwell) 攀 2 Φ Φ RDF型 RF型 (Rise-Dwell-Fall) (Rise-Fall)
凸轮运动4种类型 概 RDFD型 (Rise-Dwell-Fall-Dwell) RFD型 (Rise-Fall-Dwell) 概 述 RF型 (Rise-Fall) RDF型 (Rise-Dwell-Fall)

凸轮设计过程 1.从动件运动设计 根据凸轮机构指定的升程、回程及停歇要求, 设计从动件时序图,确定从动件运动规律 2. 凸轮机构选型 从动件运动设计 根据机构运动要求,选择适用的凸轮与从动 件类型 考虑几何尺寸限制、环境及成本要求 蟋 凸轮机构选型 3.机构参数设计 确定凸轮机构参数(基圆、最大压力角、滚 子半径/平底宽度等) 机构参数设计 4.凸轮廓线求解 利用图解法或解析法设计凸轮廓线 凸轮廓线求解 5.机构性能分析校核 分析凸轮机构的压力角、曲率半径、尺寸约 束等 机构性能校核
凸轮设计过程 1. 从动件运动设计 根据凸轮机构指定的升程、回程及停歇要求, 设计从动件时序图 确定从动件 动规律 设计从动件时序图,确定从动件运动规律 2. 凸轮机构选型 根据机构运动要求 选择适用的凸轮与从动 从动件运动设计 根据机构运动要求,选择适用的凸轮与从动 件类型 考虑几何尺寸限制、环境及成本要求 概 凸轮机构选型 3. 机构参数设计 确定凸轮机构参数(基圆、最大压力角、滚 凸轮机构选型 机构参数设计 概 述 子半径/平底宽度等) 4. 凸轮廓线求解 机构参数设计 利用图解法或解析法设计凸轮廓线 5. 机构性能分析校核 凸轮廓线求解 分析凸轮机构的压力角、曲率半径、尺寸约 束等 机构性能校核
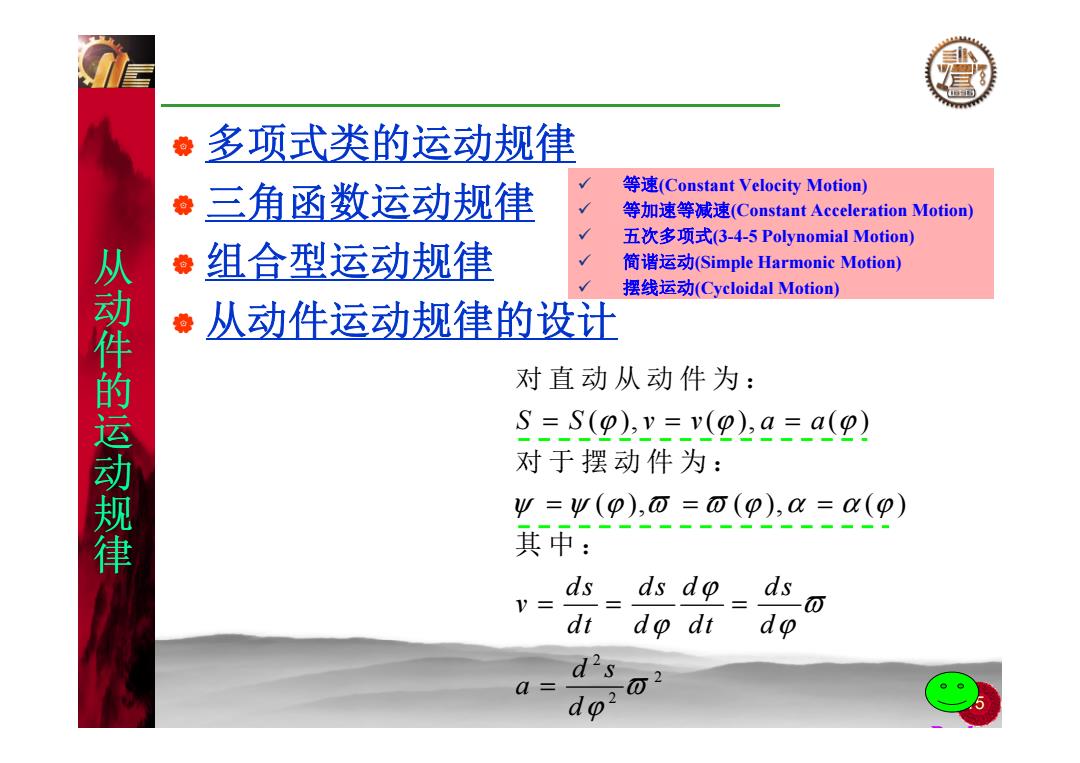
多项式类的运动规律 三角函数运动规律 等速(Constant Velocity Motion) 等加速等减速(Constant Acceleration Motion) 五次多项式(3-4-5 Polynomial Motion) ·组合型运动规律 简谐运动(Simple Harmonic Motion) 摆线运动(Cycloidal Motion) 从动件的运动规律 从动件运动规律的设计 对直动从动件为: S=S(p).v-v(o)a=a(g) 对于摆动件为: Ψ=Ψ(p),而=而(p),=x(p) 其中: ds ds do ds V= dt do dt do d2s a 2 do 5
多项式类的运动规律 三角函数运动规律 等速(Constant Velocity Motion) 等加速等减速(Constant Acceleration Motion) 从 动 三角函数运动规律 组合型运动规律 等加速等减速(Constant Acceleration Motion) 五次多项式(3-4-5 Polynomial Motion) 简谐运动(Simple Harmonic Motion) 动 摆线 运 动(C ycloidal Motion) 件 的 动 从动件运动规律的设计 对直动从动件为: 摆线 动(y ) 的 运 动 的 S S vv aa === ( ), ( ), ( ) ϕϕ ϕ 对直动从动件为: 动 对于摆动件为: 规 律 动 ψ ψϕ === ( ), ( ), ( ) ϖ ϖ ϕ α α ϕ 对于摆动件为: 其中: 律 ds ds d ds v dt d dt d ϕ ϖ ϕ ϕ == = 其中: 15 B k 2 2 2 d s a d ϖ ϕ =