1理想介质中的均匀平面波 。固定某个时刻t=t E,=E cos((ot-kz+po) E1=to ·可见在此时刻场的大小沿之方向正弦分布,相位随之 增加连续滞后。 11
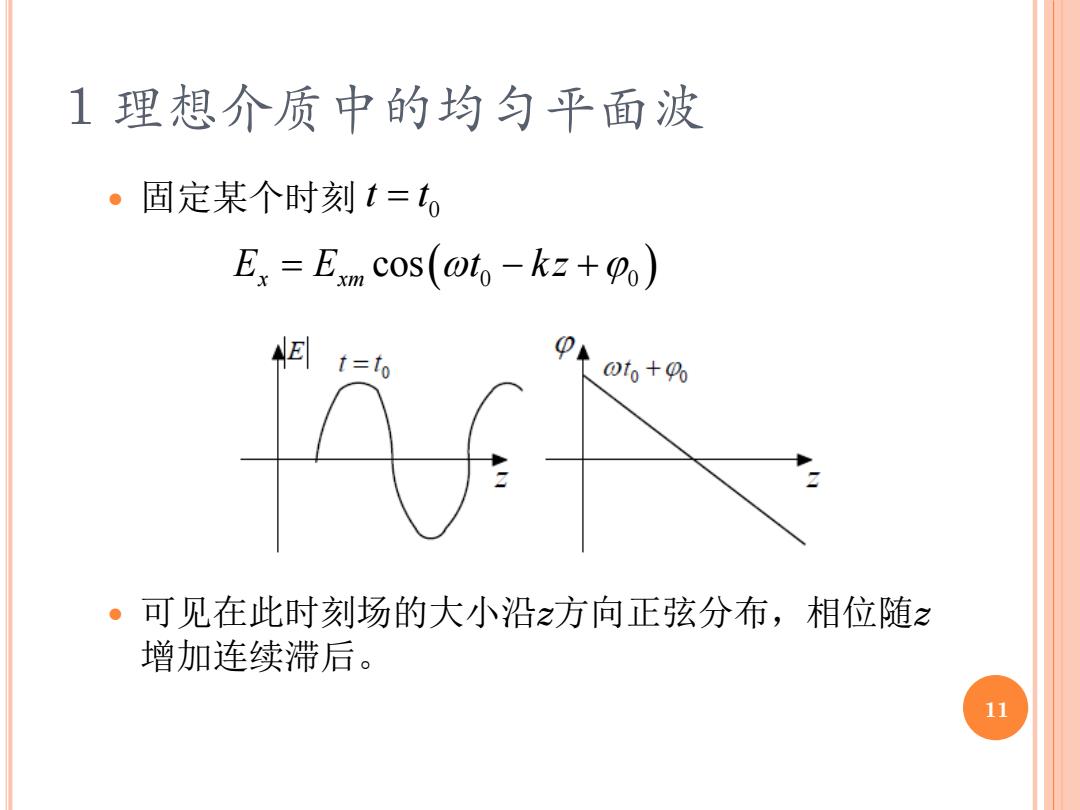
1 理想介质中的均匀平面波 固定某个时刻 可见在此时刻场的大小沿z方向正弦分布,相位随z 增加连续滞后。 0 t t = E E t k z x xm = − + cos( 0 0 ) 11

1理想介质中的均匀平面波 。相速、波长和相移常数 ·相速—等相位面移动的速度。 0t-kz+p=C或0t1-k31+p=0t2-k22+90 dz o 1 dt k ue ·波长:波在一个周期内传播的距离。 VT= 九= 12
1 理想介质中的均匀平面波 相速、波长和相移常数 相速——等相位面移动的速度。 波长:波在一个周期内传播的距离。 0 t k z C − + = 1 1 0 2 2 0 或 t k z t k z − + = − + 1 p d z v dt k = = = p p v v T f = = 12

1理想介质中的均匀平面波 相移常数:由相位的表达式,飞表示在传播方向上经 过单位距离相位的变化量,故称为相移常数。 0 k=0√u8= 2π 可见k又表示相位变化2π时,经过的波长的个数,故 又称波数。 13
1 理想介质中的均匀平面波 相移常数:由相位的表达式, 表示在传播方向上经 过单位距离相位的变化量,故称为相移常数。 可见 又表示相位变化 时,经过的波长的个数,故 又称波数。 2 p k v f = = = =k k 2 13

1理想介质中的均匀平面波 。能量密度与能流 H =门 E,=Em cos(ot-kz+g) H,=Ecos(of-kz+a,) B:D-3c 14
1 理想介质中的均匀平面波 能量密度与能流 ∵ ∴ x y E H = x y E H = E E t k z x xm = − + cos( 0 ) cos( 0 ) xm y E H t k z = − + 1 1 2 2 2 w E D E e x = = 1 1 2 2 2 w B H H m y = = 14

1理想介质中的均匀平面波 .co =Wm w=w。+wm=EE=H3 ·均匀平面波的电场能量密度和磁场能量密度相等。 S=E×i=a,E×a,H,=aEH,=anH (*) 15
1 理想介质中的均匀平面波 ∴ 均匀平面波的电场能量密度和磁场能量密度相等。 ( ) 2 2 1 1 1 2 2 2 2 w H H H w e y y y m = = = = 2 2 w w w E H e m x y = + = = 2 x x y y z x y z y S E H a E a H a E H a H = = = = (*) 15