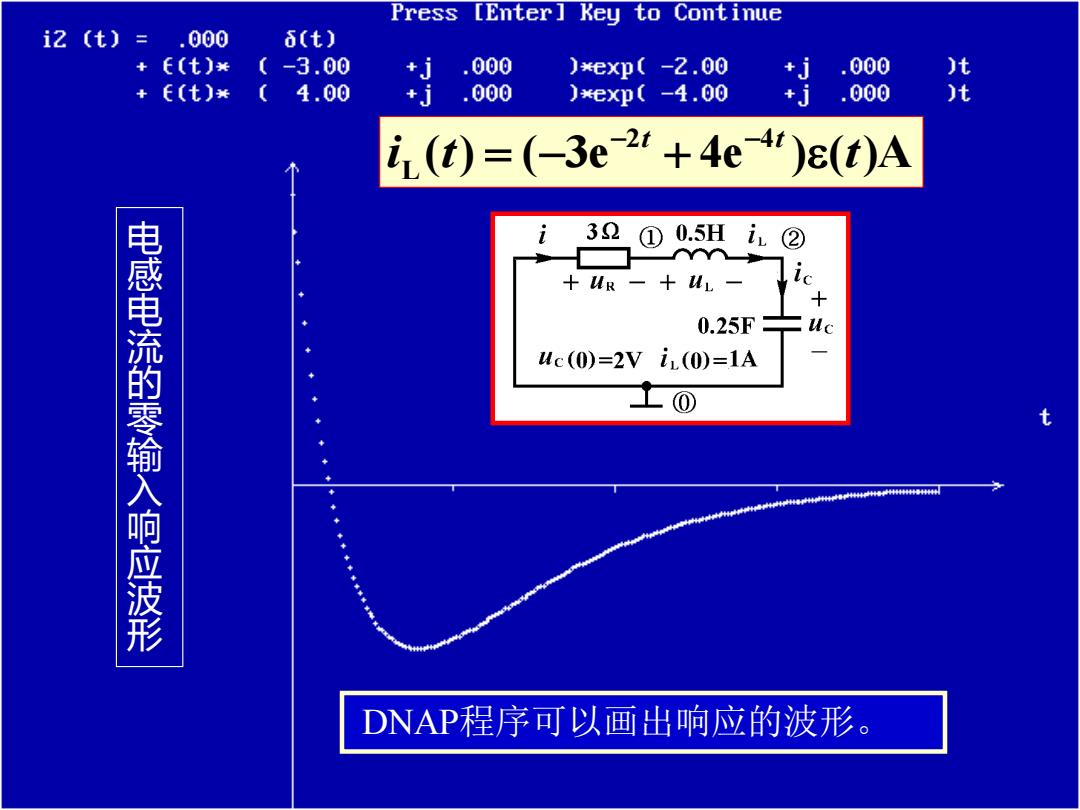
Press [Enter]Key to Continue i2〔t)=.000 (t) E(t)* (-3.00 +j .000 )exp(-2.00 .000 + E(t)* 4.00 +j .000 )exp(-4.00 +j .000 是 i(t))=(-3e2r+4e4“)e(t)A 32 ① 0.5HiL② +R-+L一 ic 电感电流的零输入响应波形 + 0.25F= uc uc(0)=2ViL(0)=1A DNAP程序可以画出响应的波形
DNAP程序可以画出响应的波形。 ( ) ( 3 e 4 e ) ( )A 2 4 Li t t t t = − + − − 电感电流的零输入响应波形

三、临界情况 当= 时,电路的固有频率,S2为两个相同的实 数s,=S,=s。齐次微分方程的解答具有下面的形式 uc(t)=K e +K,te" (9-8) 式中的两个常数K,,K由初始条件i(0)和4c(0)确定。 令式(9-5)中的0得到 uc(0)=K (9-9)
三、临界情况 当 时,电路的固有频率s1 , s2为两个相同的实 数s1 =s2 =s 。齐次微分方程的解答具有下面的形式 C L R = 2 ( ) e e (9 8) C = 1 + 2 − s t s t u t K K t 式中的两个常数K1,K2由初始条件iL (0)和uC (0) 确定。 令式(9-5)中的t=0得到 (0) (9 9) uC = K1 −

对式(9-5)求导,再令得到 duc() =0=K1S+K2= (0) (9-10 dt 联立求解以上两个方程,可以得到 K1=uc(0) K,= 2-S1uc(0) C 将K,K的计算结果,代入式(9-8)得到电容电压 的零输入响应,再利用KCL方程和电容的VCR可以得到电 感电流的零输入响应
联立求解以上两个方程,可以得到 (0) (0) (0) 1 C L 2 1 C s u C i K K u = − = 将 K1 , K2的计算结果,代入式(9-8)得到电容电压 的零输入响应,再利用KCL方程和电容的VCR可以得到电 感电流的零输入响应。 对式(9-5)求导,再令得到 (9 10) (0) d d ( ) L 0 1 2 C = = + = − C i K s K t u t t
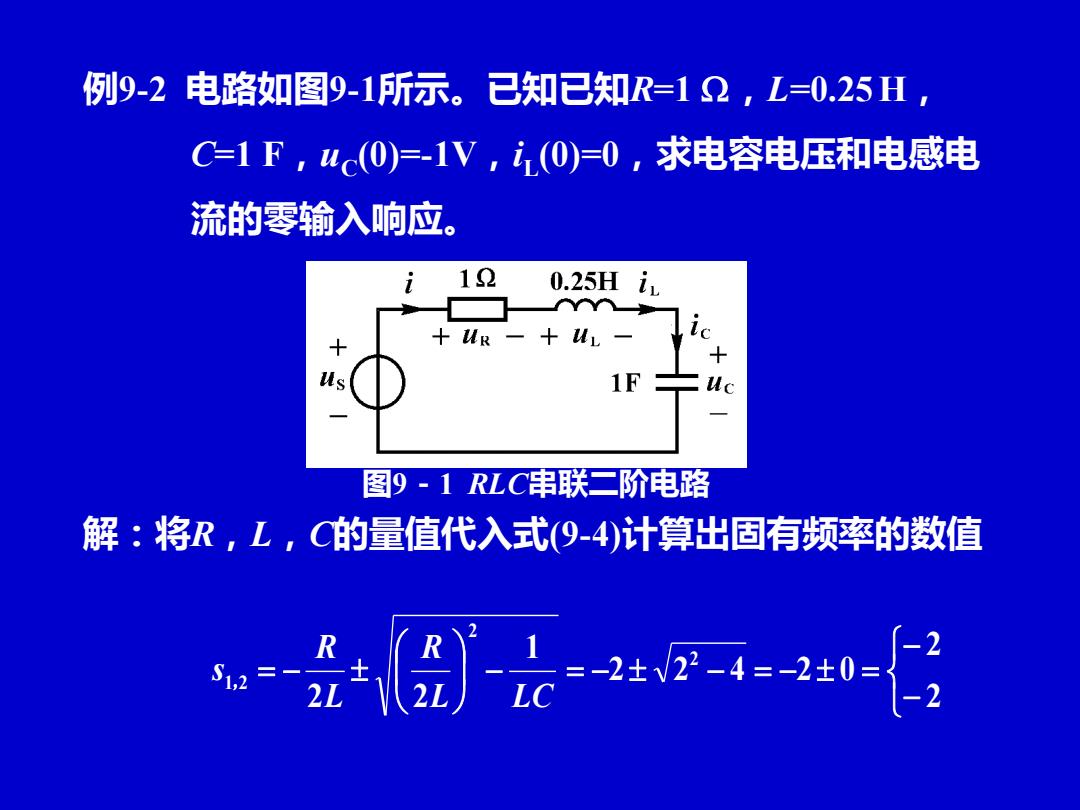
例9-2电路如图9-1所示。已知已知R=12,L=0.25H, C=1F,uc0)=-1V,i(0)=0,求电容电压和电感电 流的零输入响应。 12 0.25Hi 1F 图9-1RLC串联二阶电路 解:将R,L,C的量值代入式(9-4)计算出固有频率的数值 R 1,2
例9-2 电路如图9-1所示。已知已知R=1 ,L=0.25 H, C=1 F,uC (0)=-1V,iL (0)=0,求电容电压和电感电 流的零输入响应。 − − − = − − = − = = − 2 2 2 2 4 2 0 1 2 2 2 2 1 2 L LC R L R s , 解:将R,L,C的量值代入式(9-4)计算出固有频率的数值 图9-1 RLC串联二阶电路

将两个相等的固有频率、=S2=-2代入式(9-8)得到 u(t)=Kje +K,te2 (t≥0) 利用电容电压的初始值4。(0)=-1V和电感电流的初始值 (0)=0得到以下两个方程 uc(0)=K,=-1 @=-2K,+K,=40=0 dt
利用电容电压的初始值uC (0)=-1V和电感电流的初始值 iL (0)=0得到以下两个方程 0 (0) 2 d d ( ) (0) 1 L 0 1 2 C C 1 = − + = = = = − = C i K K t u t u K t 将两个相等的固有频率s1 =s2 =-2 代入式(9-8)得到 ( ) e e ( 0) 2 2 2 c = 1 + − − u t K K t t t t