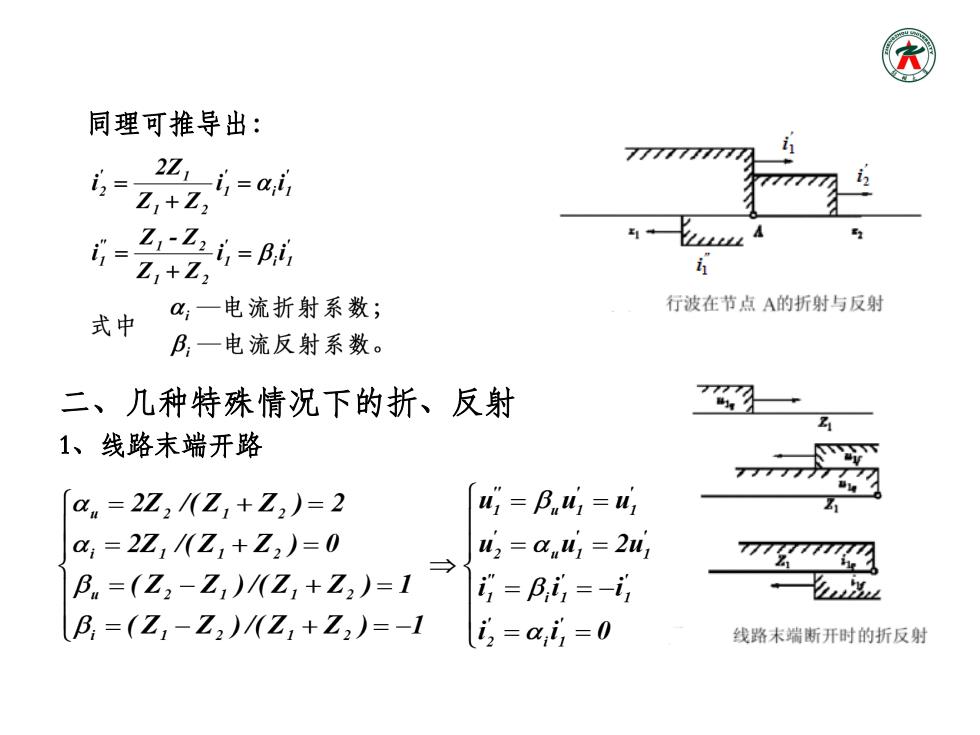
同理可推导出: 7777777777 i2= 2Z1i,=ari 777 Z1+Z2 或=Z:i=B赋 Z1+Z2 ☑一电流折射系数; 行波在节点A的折射与反射 式中 B一电流反射系数。 二、几种特殊情况下的折、反射 Z 1、线路末端开路 am=2Z2(Z,+Z2)=2 41=阝n4=4 a=2Z1/八Z,+Z2)=0 u2=an41=241 R.=(2,-Z,Z,+Z)=1→G=所=式 B=(Z,-Z2)/八Z,+Z2)=-1 3=a,i=0 线路末端断开时的折反射
同理可推导出: 二、几种特殊情况下的折、反射 1、线路末端开路

2、线路末端短路 an=2Z2(Z1+Z2)=0 41=Bn41=-41 a,=2Z1八Z,+Z2)=2 42=an41=0 B,=Z,-Z,)1Z,+Z=-1 =B,i= B:=(Z,-Z2)/八Z,+Z2)=1 =a,i=2 线路末端短路时的折反射 3、线路末端接负载电阻R(R=Z1) 7777 相当于Z2=Z1,此时a=1,B=0; 因此42=47,41=0。 线路末端接有电阻R 通讯领域称为匹配
2、线路末端短路 3、线路末端接负载电阻R(R=Z1) 通讯领域称为匹配 线路末端接有电阻R
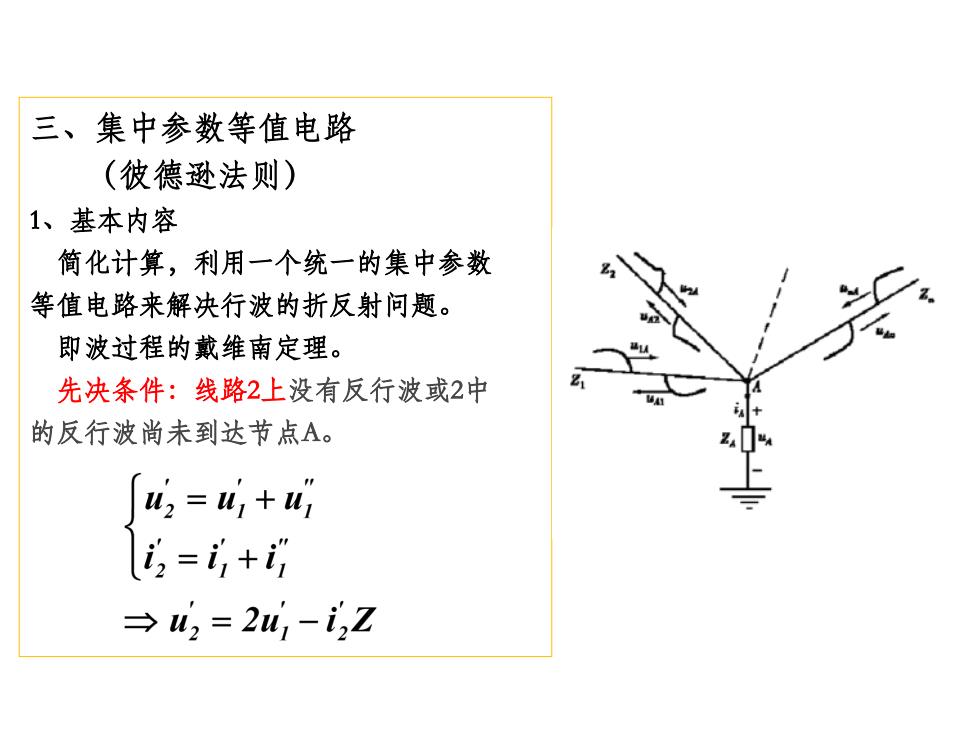
三、集中参数等值电路 (彼德逊法则) 1、基本内容 简化计算,利用一个统一的集中参数 等值电路来解决行波的折反射问题。 即波过程的戴维南定理。 先决条件:线路2上没有反行波或2中 的反行波尚未到达节点A。 42=4,+4 i,=i,+访 →2=2w1-i2Z
三、集中参数等值电路 (彼德逊法则) 1、基本内容 简化计算,利用一个统一的集中参数 等值电路来解决行波的折反射问题。 即波过程的戴维南定理。 先决条件:线路2上没有反行波或2中 的反行波尚未到达节点A
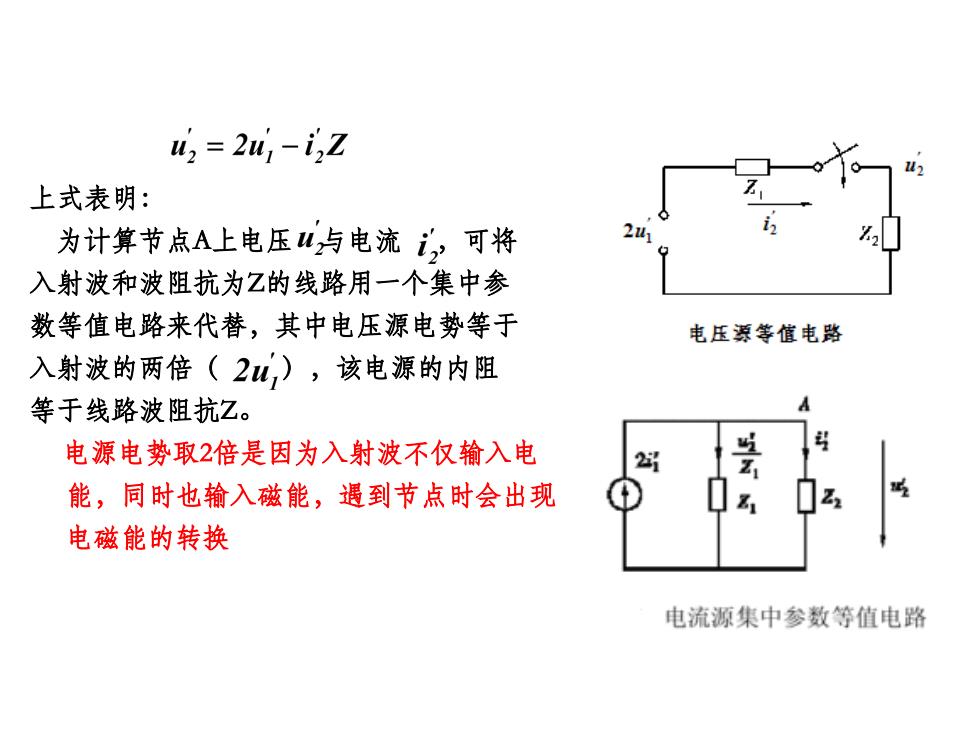
2=2u,-i2Z 上式表明: 为计算节点A上电压4与电流i,)可将 入射波和波阻抗为Z的线路用一个集中参 数等值电路来代替,其中电压源电势等于 电压源等值电路 入射波的两倍(2山),该电源的内阻 等于线路波阻抗乙。 电源电势取2倍是因为入射波不仅输入电 3 能,同时也输入磁能,遇到节点时会出现 电磁能的转换 电流源集中参数等值电路
上式表明: 为计算节点A上电压 与电流 ,可将 入射波和波阻抗为Z的线路用一个集中参 数等值电路来代替,其中电压源电势等于 入射波的两倍( ),该电源的内阻 等于线路波阻抗Z。 电源电势取2倍是因为入射波不仅输入电 能,同时也输入磁能,遇到节点时会出现 电磁能的转换
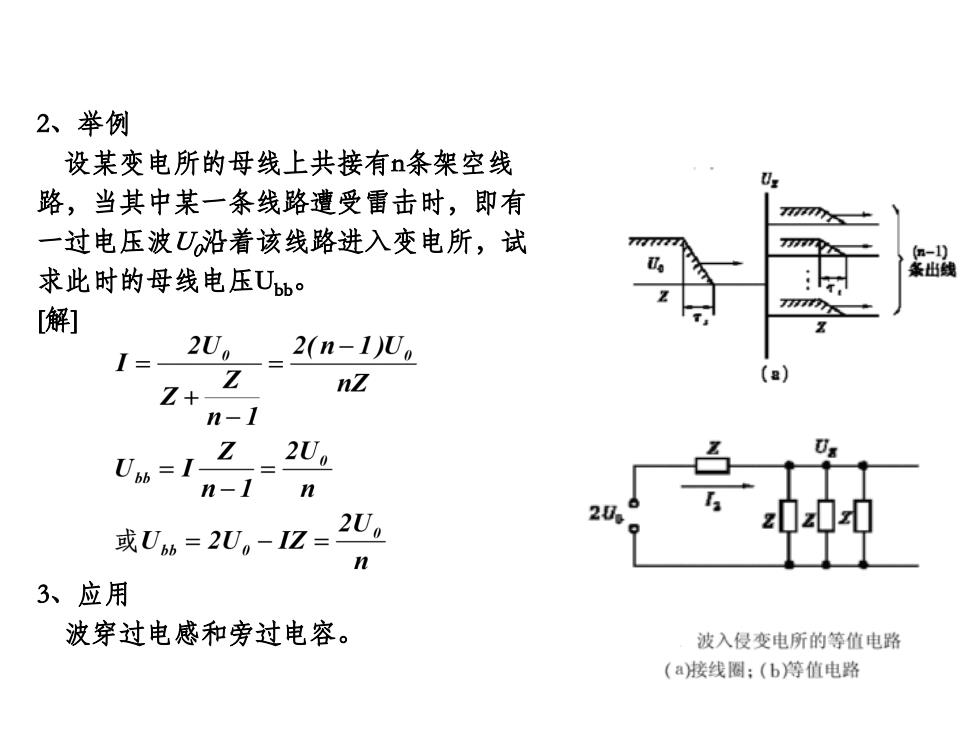
2、举例 设某变电所的母线上共接有n条架空线 路,当其中某一条线路遭受雷击时,即有 一过电压波U沿着该线路进入变电所,试 a77 a-) 求此时的母线电压Ubb 条出线 [解] rのs I= 2U。_2(n-1)Un Z nZ n-1 U=12=2U n-I n 或U=2U,-1z=2U。 20 n 3、应用 波穿过电感和旁过电容。 波入侵变电所的等值电路 (a接线圈:(b)等值电路
2、举例 设某变电所的母线上共接有n条架空线 路,当其中某一条线路遭受雷击时,即有 一过电压波U0沿着该线路进入变电所,试 求此时的母线电压Ubb。 [解] 3、应用 波穿过电感和旁过电容