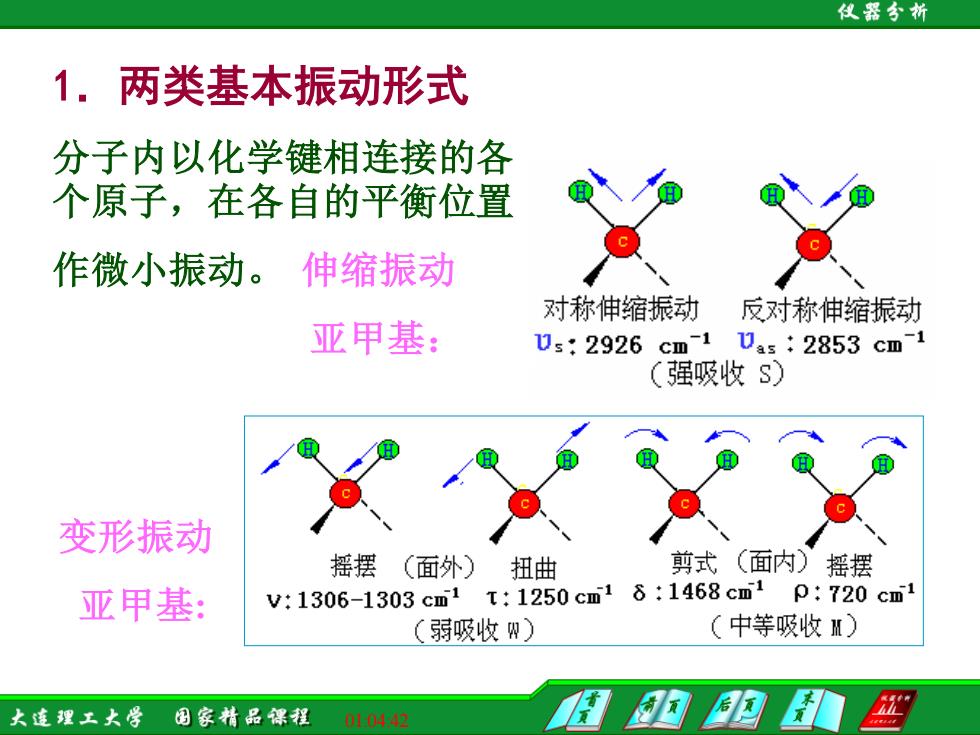
仪器令析 1.两类基本振动形式 分子内以化学键相连接的各 个原子,在各自的平衡位置 作微小振动。伸缩振动 对称伸缩振动 反对称伸缩振动 亚甲基: 0s:2926cm-1Uas:2853cm1 (强吸收S) 变形振动 摇摆(面外)扭曲 剪式(面内)摇摆 亚甲基: v:1306-1303cm1T:1250cm1δ:1468cm1p:720cm1 (弱吸收) (中等吸收M) 大连理王大学 国家精品裸程142
01:04:42 1.两类基本振动形式 分子内以化学键相连接的各 个原子,在各自的平衡位置 作微小振动。 伸缩振动 亚甲基: 变形振动 亚甲基:

仪器分析 二氧化碳的振动类型及振动频率 00-0-0-00-0-0⊙-0-0 对称伸缩 不对称伸缩 面内弯曲 面外弯曲 :1388cm1 .:2349cm 6:667cm1 y:667 cm- 图10-6 C0,分子的简正振动形式 C02分子: 四种振动类型,两个吸收峰。 (对称振动无红外活性<偶极矩没有变化>,两变 形振动吸收峰简并) 大连理王大学国家精品裸程 D10442
01:04:42 二氧化碳的振动类型及振动频率 图10-6 CO2分子: 四种振动类型,两个吸收峰。 (对称振动无红外活性<偶极矩没有变化>,两变 形振动吸收峰简并)

仪器多析 不同的基团有不同的振动频率。由经典力学可导出双 原子分子的分子振动方程式: 臣日 k为化学键的力常数(N/cm=mdyn/A) 4=(%+m,) 为基团中原子的折合质量 mm 因此,随着化学键强度增加,基团频率将增大;随着 基团原子折合质量增大,振动频率减少。 大连理王大学 国家精品裸程 0川442
01:04:42 不同的基团有不同的振动频率。由经典力学可导出双 原子分子的分子振动方程式: 1 2 1 2 ( ) m m m + m = k k c 1307 2 1 1 = = = k为化学键的力常数(N/cm = mdyn/Å) 为基团中原子的折合质量 因此,随着化学键强度增加,基团频率将增大;随着 基团原子折合质量增大,振动频率减少

仪器分析 a)影响基本振动跃迁的波数(或频率)的直接因 素为化学键力常数k和双原子折合质量μ k大,化学键的振动波数高,如 kc=c(2222cm-)>kcc(1667cm)>kc-c(1429cm1)(质 量相近) 质量μ大,化学键的振动波数低,如 μc-c(1430cm1)<μc-N(1330cm)<μc-o(1280cm )(力常数相近) 大连理工大学国家精品裸程 D10442
01:04:42 a)影响基本振动跃迁的波数(或频率)的直接因 素为化学键力常数k 和双原子折合质量 。 k大,化学键的振动波数高,如 kCC(2222cm-1)>kC=C(1667cm-1)>kC-C(1429cm-1)(质 量相近) 质量大,化学键的振动波数低,如 C-C(1430cm-1)< C-N(1330cm-1)< C-O(1280cm- 1)(力常数相近)

仪器令析 b)、经典力学导出的波数计算式为近似式。 因为振动能量变化是量子化的,同时分子 中各基团之间、化学键之间会相互影响, 因此,分子振动的波数还与分子结构(内 因)和所处的化学环境(外因)有关。 例如:C-H键基频振动的计算值为2920 cm1,而实测值为2915cm1 大连理工大学国家精品裸程 01442
01:04:42 b)、经典力学导出的波数计算式为近似式。 因为振动能量变化是量子化的,同时分子 中各基团之间、化学键之间会相互影响, 因此,分子振动的波数还与分子结构(内 因)和所处的化学环境(外因)有关。 例如:C-H键基频振动的计算值为2920 cm-1 ,而实测值为2915 cm-1