
信号与系统s1 GNALSA8rsT里Ms 5.一维信号与多维信号 信号可以表示为一个或多个变量的函数,称为一维 或多维函数。 本课程只研究一维信号,且自变量多为时间。 6.因果信号 若当t<0时f(t)=0,当t>0时f(t)卡0的 信号,称为因果信号。 而若t<0时f(t)>0,t≥0,f(t)=0的信号 称为反因果信号。 注意非因果信号指的是在时间零点之前有非零值
5.一维信号与多维信号 信号可以表示为一个或多个变量的函数,称为一维 或多维函数。 本课程只研究一维信号,且自变量多为时间。 6.因果信号 若当 t <0 时 f (t)=0, 当 t >0 时 f (t) ≠0的 信号,称为因果信号。 而若t <0 时 f (t)>0 ,t ≥ 0, f(t) =0的信号 称为反因果信号。 注意非因果信号指的是在时间零点之前有非零值
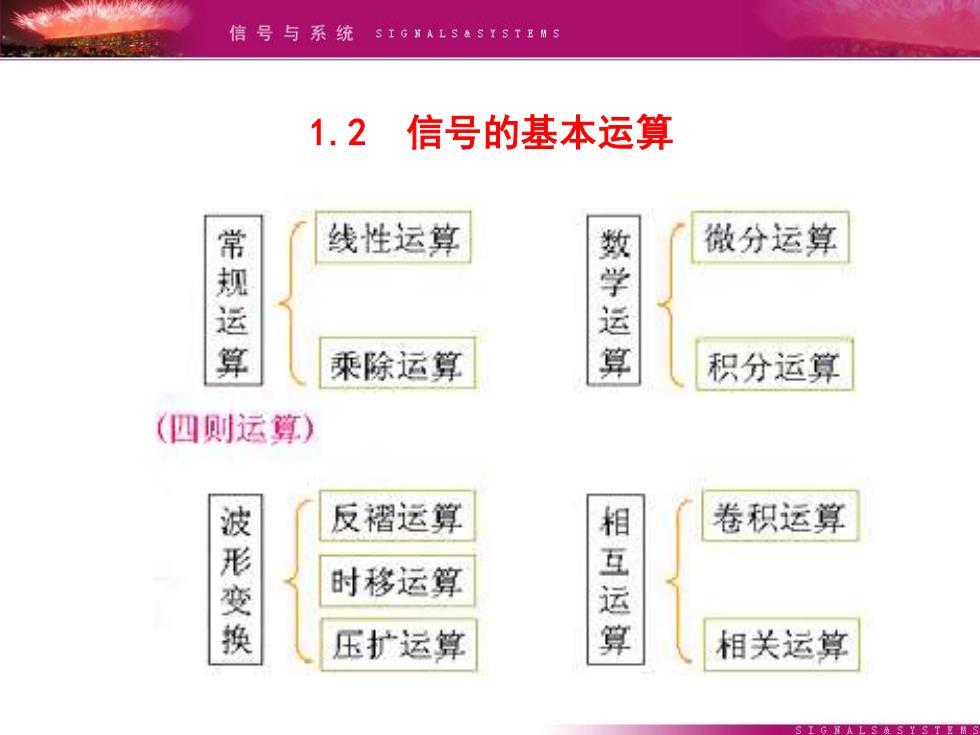
信号与系统s1GALS48r8TgMs 1.2信号的基本运算 线性运算 微分运算 常规运算 乘除运算 学运算 积分运算 (四则运算) 反褶运算 卷积运算 波形变换 相 时移运算 压扩运算 互运算 相关运算
1.2 信号的基本运算

信号与系统s1 G NALSASTST里Ms 一父信号的十、一、必运算 两信号f1()和f2()的相+、一、×指同一 时刻两信号之值对应相加减乘。如 ↑f() ↑f()+f2(t0) f()×f() S工GALS放SST2S
( ) 1 f t 1 0 1 t ( ) 2 f t 1 0 1 t ( ) ( ) 1 2 f t + f t 1 0 1 t 2 ( ) ( ) 1 2 f t f t 1 0 1 t 一、信号的+、-、×运算 两信号f1(·) 和f2 (·)的相+ 、-、×指同一 时刻两信号之值对应相加减乘。如

信号与系统s1GALS48r8TgMs 三、信号的时间变换运算 1.平移 将f(t)→f(t+t0).,f(k)→f(t+k0)称为对 信号f()的平移或移位。若t0(或k0)<0,则将f()右移; 否则左移。 lf(t+1) 1f(t-1) 0 f(t+to)将f(①超前 f(tto)将f①)延迟 时间to;即将f(t 时间to;即将f(t 的波形向左移动o 的波形向右移动to
f (t) 1 0 1 t f (t +1) 1 −1 0 t f (t −1) 1 0 1 2 t 二、信号的时间变换运算 1. 平移 将f (t) → f (t + t0) , f (k) → f (t + k0)称为对 信号f (·)的平移或移位。若t0 (或k0)< 0,则将f (·)右移; 否则左移。 f (t-t0)将 f (t) 延迟 时间 t0 ;即将 f (t) 的波形向右移动 t0 。 f (t+t0)将 f (t) 超前 时间 t0 ;即将 f (t) 的波形向左移动 t0

信号与系统s1 GNALSA8 YSTENS 2反转 将f(t)→f(-t),f(k)→f(-k)称 为对信号f()的反转或反折。从图形上看是将f() 以纵坐标为轴反转180。如 f(-t)
2. 反转 将f (t) → f (– t) , f (k) → f (– k) 称 为对信号f (·)的反转或反折。从图形上看是将f (·) 以纵坐标为轴反转180o。如 f (t) 1 0 1 t f (−t) −1 0 t