
1-2变形固体的基本假设 ↓变形固体(Deformable Body):在力的作用下,会发生 变形的固体。 变形固体的基本假设: 均匀假设(Uniformity) 连续假设(Continuity) 各向同性假设(Isotropy) 小变形假设(Small Deformation) ■变形Deformation):构件受力后,形状或尺寸发生的改变 ■弹性变形(Elastic Deformation):卸载时能够消失或恢复的变形 塑性变形Plastic Deformation):卸载时不能消失或恢复的变形
变形固体(Deformable Body) :在力的作用下,会发生 变形的固体。 变形固体的基本假设: 均匀假设 (Uniformity) 连续假设 (Continuity) 各向同性假设 (Isotropy) 小变形假设 (Small Deformation) 1-2 变形固体的基本假设 变形(Deformation) :构件受力后,形状或尺寸发生的改变 弹性变形(Elastic Deformation):卸载时能够消失或恢复的变形 塑性变形(Plastic Deformation):卸载时不能消失或恢复的变形

1-2变形固体的基本假设 理论力学和材料力学的区别 《理论力学》研究物体机械运动一般规律的学科 《材料力学》研究构件承受载荷能力的学科 理论力学 材料力学 学科分类: 一般力学 固体力学 研究对象: 刚体 变形体 研究内容: 力的平衡及运动规律 物体本身的变形等 力学效应: 力作用的外效应 力作用的内效应
理论力学和材料力学的区别 理论力学 材料力学 学科分类: 一般力学 固体力学 研究对象: 刚体 变形体 研究内容: 力的平衡及运动规律 物体本身的变形等 力学效应: 力作用的外效应 力作用的内效应 《理论力学》研究物体机械运动一般规律的学科 《材料力学》研究构件承受载荷能力的学科 1-2 变形固体的基本假设

1-3内力和应力 外力(External Force):作用在构件上的所有载荷和支座 反力。 外力按形式可以分为:集中力、集中力偶、分布力和分布 力偶。 外力按性质可以分为: 静载荷(Static Force):载荷由零缓慢增加,到达某值后保 持不变; 动载荷(Dynamic Force):引起构件加速度的突加载荷或冲 击载荷; 交变载荷(Alternating Force):随时间作周期变化的载荷
外力(External Force ):作用在构件上的所有载荷和支座 反力。 外力按形式可以分为:集中力、集中力偶、分布力和分布 力偶。 外力按性质可以分为: 静载荷(Static Force):载荷由零缓慢增加,到达某值后保 持不变; 动载荷(Dynamic Force):引起构件加速度的突加载荷或冲 击载荷; 交变载荷(Alternating Force):随时间作周期变化的载荷。 1-3 内力和应力

1-3内力和应力 内力nternal Force):在外力作用下,构件内各质点的相应 位置发生了变化,从而引起的各质点间相互作用力的改变量, 又称“附加内力”。 内力随外力的增加而增加,直至构件发生破坏 +截面法(Method of Section)是确定内力的一种方法; (1)一分为二(2)去一留一(3)平衡求解 ∑F=0R=F 内力在截面上是连续分布的,截面法只能确定截面上分布内 力的合力(或合力偶矩)
内力(Internal Force) :在外力作用下,构件内各质点的相应 位置发生了变化,从而引起的各质点间相互作用力的改变量, 又称“附加内力”。 内力随外力的增加而增加,直至构件发生破坏; 截面法(Method of Section)是确定内力的一种方法; (1)一分为二 (2)去一留一 (3)平衡求解 F F F FN N 0 Fx F F 1-3 内力和应力 内力在截面上是连续分布的,截面法只能确定截面上分布内 力的合力(或合力偶矩)
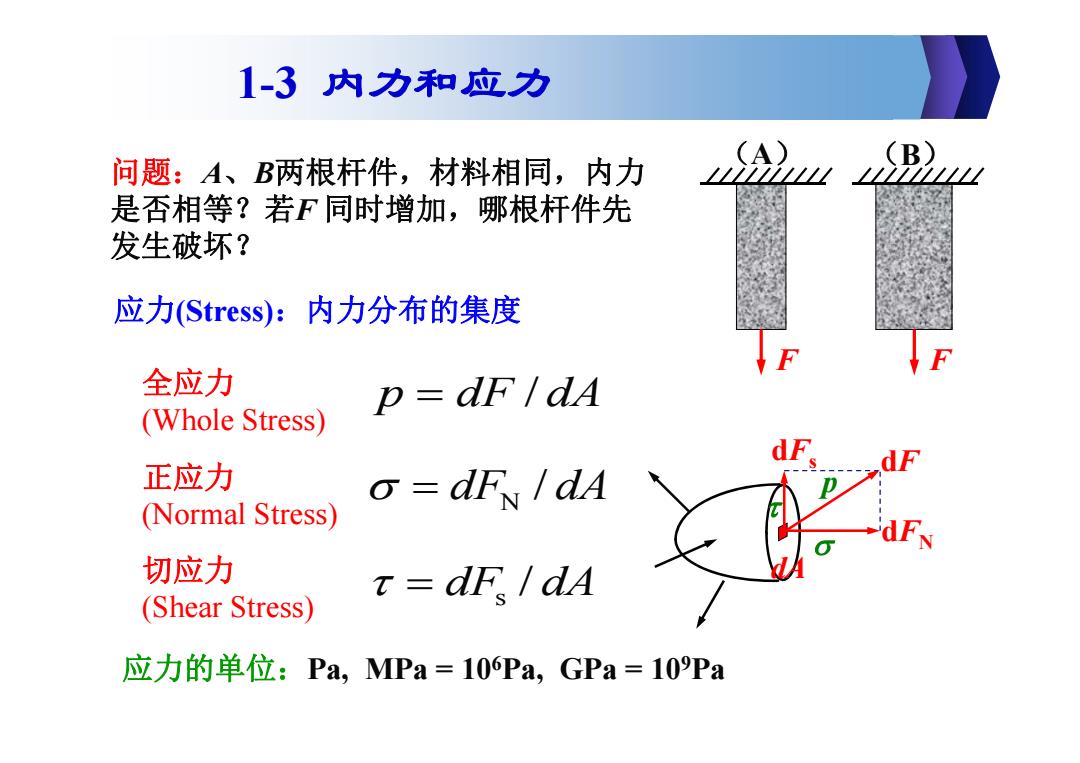
1-3内力和应力 问题:A、B两根杆件,材料相同,内力 A》uB2山 是否相等?若F同时增加,哪根杆件先 发生破坏? 应力(Stress):内力分布的集度 全应力 p=dF/dA (Whole Stress) 正应力 (Normal Stress) o=dFI dA 切应力 t=dF.I dA (Shear Stress) 应力的单位:Pa,MPa=10Pa,GPa=10Pa
问题:A、B两根杆件,材料相同,内力 是否相等?若F 同时增加,哪根杆件先 发生破坏? (A) (B) F F 应力(Stress):内力分布的集度 dA 全应力 (Whole Stress) p dF / dA 正应力 (Normal Stress) N dF dA / 切应力 (Shear Stress) s dF dA / 应力的单位:Pa, MPa = 106Pa, GPa = 109Pa 1-3 内力和应力 dF p dFs dFN