
3-1-1超定方程组 当m>n时,方程个数大于未知量个数,Ax=b的解可能不存在 记目标函数: J(z)≌‖Ax-b3 全易知:J)是关于x的二次函数,而且是凸函数 多因此,,是问题(31)的解当且仅当,是Jc)的稳定点,即满足 8J =0 ←→ATAx-Ab=0 如果A不是满秩,则A「A半正定,此时解不唯一 http://math.ecnu.edu.cn/-jypan 4/26
3-1-1 超定方程组 当 m > n 时, 方程个数大于未知量个数, Ax = b 的解可能不存在. 记目标函数: J(x) ≜ ∥Ax − b∥ 2 2 易知: J(x) 是关于 x 的二次函数, 而且是凸函数. 因此, x∗ 是问题 (3.1) 的解当且仅当 x∗ 是 J(x) 的稳定点, 即满足 ∂J ∂x = 0 ⇐⇒ A ⊺ Ax − A ⊺ b = 0 ✍ 如果 A 不是满秩, 则 A ⊺A 半正定, 此时解不唯一. http://math.ecnu.edu.cn/~jypan 4/26

3-1-2欠定方程组 当m<n时,方程个数小于未知量个数,存在无穷多个解(假定A满秩),是不适定问题 http://math.ecnu.edu.cn/-jypan 5/26
3-1-2 欠定方程组 当 m < n 时, 方程个数小于未知量个数, 存在无穷多个解 (假定 A 满秩), 是不适定问题. 这时我们通常寻求最小范数解, 于是原问题就转化为下面的 约束优化问题 min Ax=b 1 2 ∥x∥ 2 2 (3.2) 对应的 Lagrange 函数为 L(x, λ) = 1 2 ∥x∥ 2 2 + λ ⊺ (Ax − b), 其中 λ = [λ1, . . . , λm] ⊺ 是 Lagrange 乘子. 问题 (3.2) 的解就是 L(x, λ) 的鞍点, 即: ∂L ∂x = x + A ⊺ λ = 0, ∂L ∂λ = Ax − b = 0. 写成矩阵形式为 [ I A ⊺ A 0 ] [ x λ ] = [ 0 b ] . 如果 A 满秩则存在唯一解. http://math.ecnu.edu.cn/~jypan 5/26

3-1-2欠定方程组 当m<时,方程个数小于未知量个数,存在无穷多个解(假定A满秩),是不适定问题 花这时我们通常寻求最小范数解,于是原问题就转化为下面的约束优化问题 盟2暇 (3.2) 对应的Lagrange函数为 C(红,)=z吃+T(Ar-), 其中入=[A1,,入mJ「是Lagrange乘子.问题(3.2)的解就是C(z,的鞍点,即: ∂c ac =Ax-b=0. Ox =E+Aλ=0, ax 写成矩阵形式为 如果A满秩则存在唯一解 http://math.ecnu.edu.cn/-jyp 5/26
3-1-2 欠定方程组 当 m < n 时, 方程个数小于未知量个数, 存在无穷多个解 (假定 A 满秩), 是不适定问题. 这时我们通常寻求最小范数解, 于是原问题就转化为下面的 约束优化问题 min Ax=b 1 2 ∥x∥ 2 2 (3.2) 对应的 Lagrange 函数为 L(x, λ) = 1 2 ∥x∥ 2 2 + λ ⊺ (Ax − b), 其中 λ = [λ1, . . . , λm] ⊺ 是 Lagrange 乘子. 问题 (3.2) 的解就是 L(x, λ) 的鞍点, 即: ∂L ∂x = x + A ⊺ λ = 0, ∂L ∂λ = Ax − b = 0. 写成矩阵形式为 [ I A⊺ A 0 ] [x λ ] = [ 0 b ] . 如果 A 满秩则存在唯一解. http://math.ecnu.edu.cn/~jypan 5/26

本课程主要讨论超定问题 http://math.ecnu.edu.cn/-jypan 6/26
本课程主要讨论 超定问题 http://math.ecnu.edu.cn/~jypan 6/26
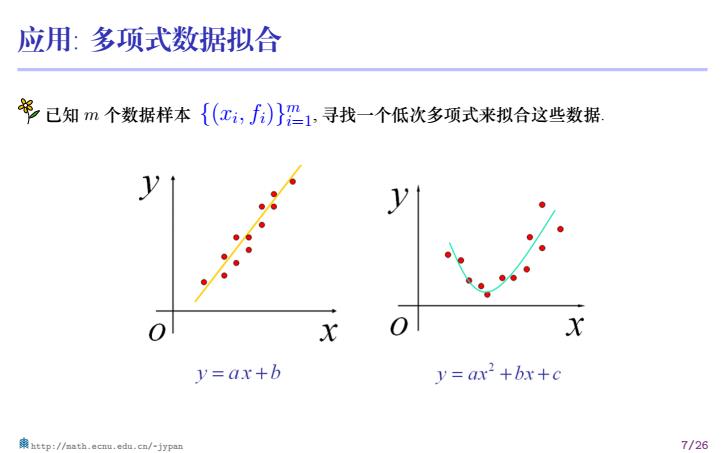
应用:多项式数据拟合 多已知m个数据样本{(x,f)}沿1,寻找一个低次多项式来拟合这些数据. X X y=ax+b y=ax2+bx+c http://nath.ecnu.edu.cn/-jypan 7/26
应用: 多项式数据拟合 已知 m 个数据样本 {(xi , fi)} m i=1, 寻找一个低次多项式来拟合这些数据. http://math.ecnu.edu.cn/~jypan 7/26