
数值分析 第二讲线性方程组的直接解法 扰动分析·解的改进 目录 2.1 Gauss消去法 2.2矩阵分解法 2.3扰动分析 AAYIAA 2.4解的改进* https://math.ecnu.edu.cn/-jypan/Teaching/NA 潘建瑜@MATH.ECNU
数值分析 第二讲 线性方程组的直接解法 扰动分析 • 解的改进 2.1 Gauss 消去法 2.2 矩阵分解法 2.3 扰动分析 2.4 解的改进 * 目录 https://math.ecnu.edu.cn/~jypan/Teaching/NA 潘建瑜 @MATH.ECNU

2-3|扰动分析 2.3扰动分析 2.3.1矩阵条件数 2.3.2条件数与扰动分析 https://math.ecnu.edu.cn/-jypan/Teaching/NA
2-3 扰动分析 2.3 扰动分析 2.3.1 矩阵条件数 2.3.2 条件数与扰动分析 https://math.ecnu.edu.cn/~jypan/Teaching/NA

2-3-1 矩阵条件数 为什么要考虑扰动分析 除了数据误差和截断误差外,在用计算机进行数值计算时,每次运算(加减乘除等)还会 产生舍入误差.对于大规模问题,实际运算次数往往非常巨大,因此直接分析舍入误差比 较复杂,而且得到的结果往往不一定能反映实际计算情况.当前一种比较实用的误差分 析方法是将舍入误差看作是对原始数据的扰动,即将其归结到数据误差中,这样就可以在 很大程度上简化误差分析过程.这种误差分析方法称为向后误差分析, 病态线性方程组/病态矩阵 考虑线性方程组Ax=b,如果A或b的微小变化(也称为扰动)会导致解的巨大变化,则 称此线性方程组是病态的,反之则是良态的 http://math.ecnu.edu.cn/-jypan 3/22
2-3-1 矩阵条件数 为什么要考虑扰动分析 除了数据误差和截断误差外, 在用计算机进行数值计算时, 每次运算 (加减乘除等) 还会 产生舍入误差. 对于大规模问题, 实际运算次数往往非常巨大, 因此直接分析舍入误差比 较复杂, 而且得到的结果往往不一定能反映实际计算情况. 当前一种比较实用的误差分 析方法是将舍入误差看作是对原始数据的扰动, 即将其归结到数据误差中, 这样就可以在 很大程度上简化误差分析过程. 这种误差分析方法称为向后误差分析. 病态线性方程组/病态矩阵 考虑线性方程组 Ax = b, 如果 A 或 b 的微小变化 (也称为 扰动) 会导致解的巨大变化, 则 称此线性方程组是 病态 的, 反之则是 良态 的. http://math.ecnu.edu.cn/~jypan 3/22

病态线性方程组举例 例考虑线性方程组Ax=b,其中A= →解为x= 20 http://math.ecnu.edu.cn/-jypan 4/22
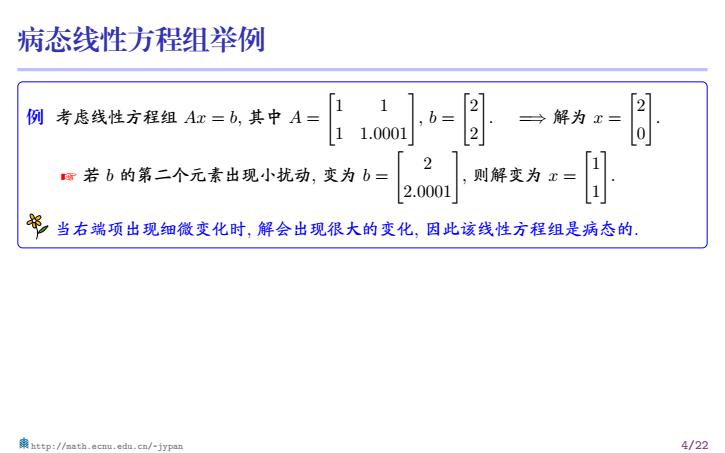
病态线性方程组举例 例 考虑线性方程组 Ax = b, 其中 A = [ 1 1 1 1.0001] , b = [ 2 2 ] . =⇒ 解为 x = [ 2 0 ] . Z 若 b 的第二个元素出现小扰动, 变为 b = [ 2 2.0001 ] , 则解变为 x = [ 1 1 ] . 当右端项出现细微变化时, 解会出现很大的变化, 因此该线性方程组是病态的. 怎样判断一个线性方程组是否病态? 对于线性方程组而言, 问题是否变态主要取决于 系数矩阵是否病态 . 判断一个矩阵是否病态的一个重要指标是 矩阵条件数 . http://math.ecnu.edu.cn/~jypan 4/22
病态线性方程组举例 1 例考虑线性方程组Ax=b,其中A= 1 ,b= 1 →解为x= 1.0001 22 20 都当右端项出现细微变化时,解会出现很大的变化,因此该线性方程组是病态的, http://nath.ecnu.edu.cn/-jypan 4/22
病态线性方程组举例 例 考虑线性方程组 Ax = b, 其中 A = [ 1 1 1 1.0001] , b = [ 2 2 ] . =⇒ 解为 x = [ 2 0 ] . Z 若 b 的第二个元素出现小扰动, 变为 b = [ 2 2.0001] , 则解变为 x = [ 1 1 ] . 当右端项出现细微变化时, 解会出现很大的变化, 因此该线性方程组是病态的. 怎样判断一个线性方程组是否病态? 对于线性方程组而言, 问题是否变态主要取决于 系数矩阵是否病态 . 判断一个矩阵是否病态的一个重要指标是 矩阵条件数 . http://math.ecnu.edu.cn/~jypan 4/22