电路的频率响应电路i(jo)i,(jo)线性[U,(j0)U,(jo)网络激励是电流源激励是电压源i,(jo)U,(jo)转移转移H(j@)福H(jo) :U,(jo)导纳阻抗i(jo)i,(ja)U,(jo)转移转移H(j@)=H(jの)=i(jo)电流比U,(jo)电压比返上回页下页
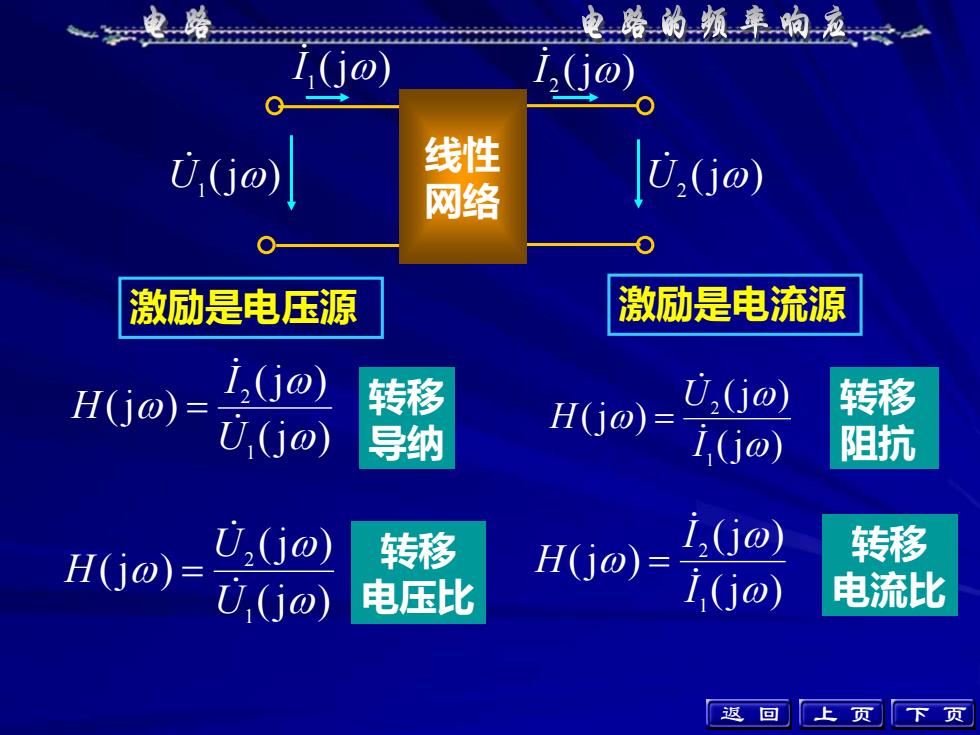
转移 导纳 转移 阻抗 转移 电压比 转移 电流比 激励是电压源 激励是电流源 (j ) U 1 线性 网络 (j ) U 2 (j ) I 1 (j ) I 2 (j ) (j ) (j ) 1 2 I U H = (j ) (j ) (j ) 1 2 U I H = (j ) (j ) (j ) 1 2 U U H = (j ) (j ) (j ) 1 2 I I H = 返 回 上 页 下 页

州电路电路的频率响应注意、输出①H(iの)与网络的结构、参数值有关,与输入、变量的类型以及端口对的相互位置有关,与输入,输出幅值无关。因此网络函数是网络性质的一种体现。是一个复数,它的频率特性分为两个部分:2) H(jの)I H(jの) ~ Q幅频特性模与频率的关系(j)~ 相频特性幅角与频率的关系网络函数可以用相量法中任一分析求解方法获得3返上回页下页
注意 H(j)与网络的结构、参数值有关,与输入、输出 变量的类型以及端口对的相互位置有关,与输入、 输出幅值无关。因此网络函数是网络性质的一种体 现。 H(j) 是一个复数,它的频率特性分为两个部分: 幅频特性 模与频率的关系 | H(j) |~ 相频特性 幅角与频率的关系 (j) ~ 网络函数可以用相量法中任一分析求解方法获得。 返 回 上 页 下 页
电路电路的频率响应例求图示电路的网络函数i,/Us和U,/Us10C十X厂2222转移导纳解列网孔方程解电流2i, /U,= 4-α° +j60(2+jo)i -2i, =U-2i, +(4+ j)l2 =0j20U,/0s=4-0 +j602Usi,= 4+(j0) +j60转移电压比返上回页下页
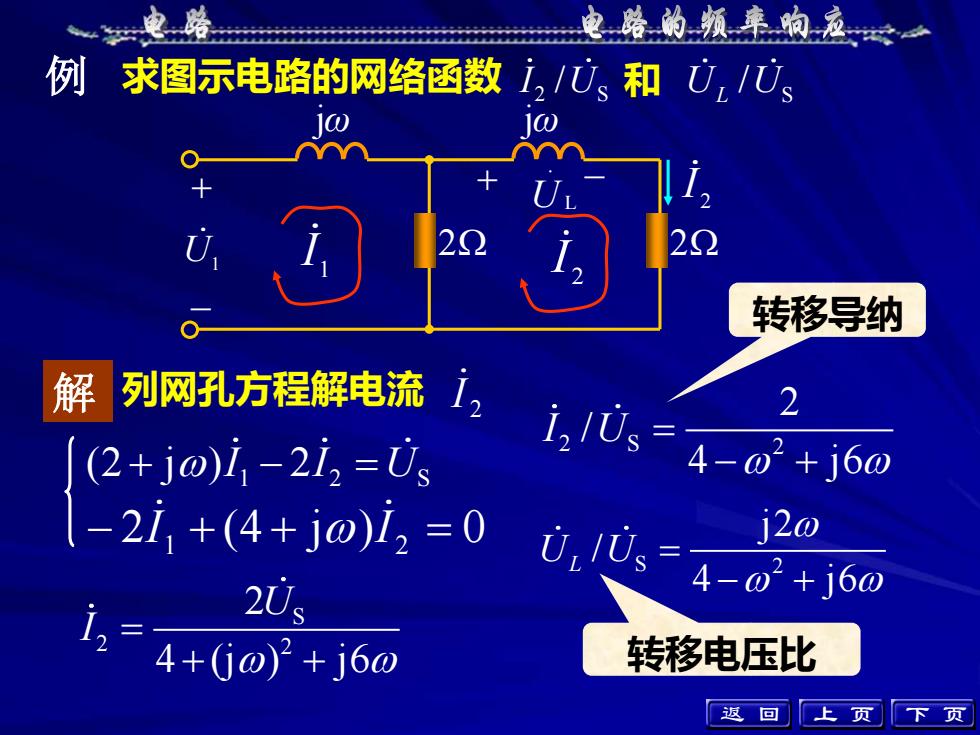
例 求图示电路的网络函数 2 S I U/ S / 和 U U L L . U U1 2 jω + _ + _ jω 2 2 I 1 I 2 I 解 列网孔方程解电流 2 I 1 2 S (2 j ) 2 + − = I I U − 2I1 + (4 + j )I 2 = 0 S 2 2 2 4 (j ) j6 U I = + + 2 S 2 2 / 4 j6 I U = − + S 2 j 2 / 4 j6 U U L = − + 转移导纳 转移电压比 返 回 上 页 下 页

电路的频率响应注意(②以网络函数中@的最高次方的次数定义网络函数的阶数。②由网络函数能求得网络在任意正弦输入时的端口正弦响应,即有R(jo)H(jの)=R(jo)= H(jo)E(jo)E(jo)返上回页下页
①以网络函数中jω的最高次方的次数定义网络 函数的阶数。 R(j) H(j)E(j) = 注意 ②由网络函数能求得网络在任意正弦输入时 的端口正弦响应,即有 (j ) (j ) (j ) E R H = 返 回 上 页 下 页

电路电路的频率响应11.2RLC串联电路的谐振谐振是正弦电路在特定条件下产生的一种特殊物理现象。谐振现象在无线电和电工技术中得到广泛应用,研究电路中的谐振现象有重要实际意义,1.谐振的定义含R、L、C的一端口电路,在特定条件下出现端口电压、电流同相位的现象时,称电路发生了谐振发生乙一R,L,CT=Z=R谐振电路返上回页下页
11.2 RLC串联电路的谐振 谐振是正弦电路在特定条件下产生的一种特殊物 理现象。谐振现象在无线电和电工技术中得到广泛 应用,研究电路中的谐振现象有重要实际意义。 含R、L、C的一端口电路,在特定条件下出现端口 电压、电流同相位的现象时,称电路发生了谐振。 1. 谐振的定义 R,L,C U 电路 I Z R I U = = 发生 谐振 返 回 上 页 下 页