
6 第一章行列式 x-10.0 0 0 x-1.0 0 (5) =a.x+-1x-1+.+a1x+an 000 -1 ao a1 a2.a-la |a2-62ab-62b2 |(a-b2b-662 正0左式a2a-2ba0。-62b c2-C3 001 0 01 =(a-b)3=右式: (2)将左式按第1列拆开得 ax ay+bz ax+br by ay+bz az+bx 左式=ayaz+bxax+by+bzaz+brax+by=aD,+bD2, az ax+by ay+bz bx ax+by ay+bz x ay+bz az+br x ay+bz z 其中 D=y ax+bt ax+byaa y az+br 之ax+byay+br z ax+by y c3-c, x y z c2÷a -a y zz i zz y y ay+bz az+br y z az+bx D2=z az+bx ax+by 26z证+的 x ax+by ay+bz x y ay+bz -a b x y z c3÷b z x y ca-c z y z zz y x y z 于是 D=aD,+bD=(a'+b)y之x=右式. :z y a22a+12a+32a+5 (3)左式6 b22b+12b+32b+5 c-cc22c+12c+32c+5 G2-c1 d22d+12d+32d+5

习题解答 17 |a22a+122 c4- c3-c2 公2b+122=0(因有两列相同): c22c+122 d22d+122 1 1 1 1 (4)左式a2n0 b-a c-a d-a r3-ar:0 b(b-a)c(c-a)d(d-a) -an ob2(62-a2)c(e-a')d'(d2-a) 1 1 1 按(展开 备各列题取公四子(b-a(c-a)(d-a)b c d b2(b+a)c2(c+a)d2(d+a) 1111 nMtan(b-a)(c-a)(d-a)o c-b d-6 r2-r1 0 z y =6-ac-ad-a)c-6d-6, xy 其中:x=c2(c+a)-(bc)(b+a)=c(c2+ac-b2-ab)=c(a+b+c)(c-b): y=d2(d+a)-bd(b+a)=d(a+b+d)(d-b). 故 c-b d-b 1 1. =(c-b)(d-b) z y c(a+b+c)d(a+b+d) =(c-b)(d-b)[d(a+b+d)-c(a+b+c)] =(c-b)(d-b)[(d-c)(a+b)+d2-c2] =(c-b)(d-b)(d-c)(a+b+c+d), 因此,左式=(b-a)(c-a)(d-a)(c-b)(d-b)(d-c)(a+b+c+d)=右式. (5)证一递推法.按第1列展开,以建立递推公式, 1-1 x-1 D1=xD.+(-1)2ao x-1 =xDn+(-1)2m+2a0=xD.+a0: 又,归纳基础为:D,=an(注意不是x),于是 D+1=xD,+o =x(xD.-1+ai)+ao

18 第一章行列式 =x2D.-1+aix+ao 日4 I"D:+a-11++aix+ao =a0+a1x+a2x2+.+anx° 证二按最后一行展开得 x-1 .-1 D.(-1)a -1 x-1 程一1 =∑(-1)2-a =0 =会o,d=w+az+a2++a+a 7.设n阶行列式D=det(aa),把D上下翻转、或逆时针旋转90°、或依副 对角线翻转,依次得 a a.a1.a.a 证明D,=D,=(-1)D,D,=D. 证(1)先计算D,为此通过交换行将D,变换成D,从而找出D,与D 的关系。 D,的最后一行是D的第1行,把它依次与前面的行交换,直至换到第1 行,共进行”-1次交换:这时最后一行是D的第2行,把它依次与前面的行交 换,直至换到第2行,共进行n-2次交换:.,直至最后一行是D的第n一1 行,再通过一次交换将它换到第”一1行,这样就把D,变换成D,共进行 (n-1)+(n-2)+.+1=2(n-1) 次交换,故D,=(-1)"D

习题解答 19 注1”上述交换行列式的行(列)的方法,在解题时,经常用到.它的特点是 在把最后一行换到某一行的同时,保持其余”-1个行之间原有的先后次序(但 行的序号可能改变).2°同理把D左右翻转所得行列式为(-1)D. (2)计算D2.注意到D2的第1,2,.,n行恰好依次是D的第n,n-1,., 1列,故若把D2上下翻转得方2,则D2的第1,2,.,n行依次是D的第1, 2,.,n列,即D2=D.于是由(1) D,=(-1)-”方2=(-1)2-"D=(-1)-vD. (3)计算D,.注意到若把D逆时针旋转90得D3,则D,的第1,2,., 列恰好是D的第,n-1,.,1列,于是再把D,左右翻转就得到D,由(1)之注 及(2),有 D,=(-1)-"D,=D. 注本例的结论值得记取,即对行列式D作转置、依副对角线翻转、旋转 180°所得行列式不变:作上下翻转、左右翻转、逆(顺)时针旋转90°所得行列式为 (-1)2-0D. 8.计算下列各行列式(D:为k阶行列式): a 1 (1)D.= ,其中对角线上元素都是a,未写出的元素都是0: 1 xa.a ax.a (2)D.=: aa .x a"(a-l)”.(a-n)” a-1(a-1-1. (a-n)-1 (3)D.1= a a-1 a-n 1 1 提示:利用范德蒙德行列式的结果, a. (4)D2.= a:b ,其中未写出的元素都是0: c di . C d
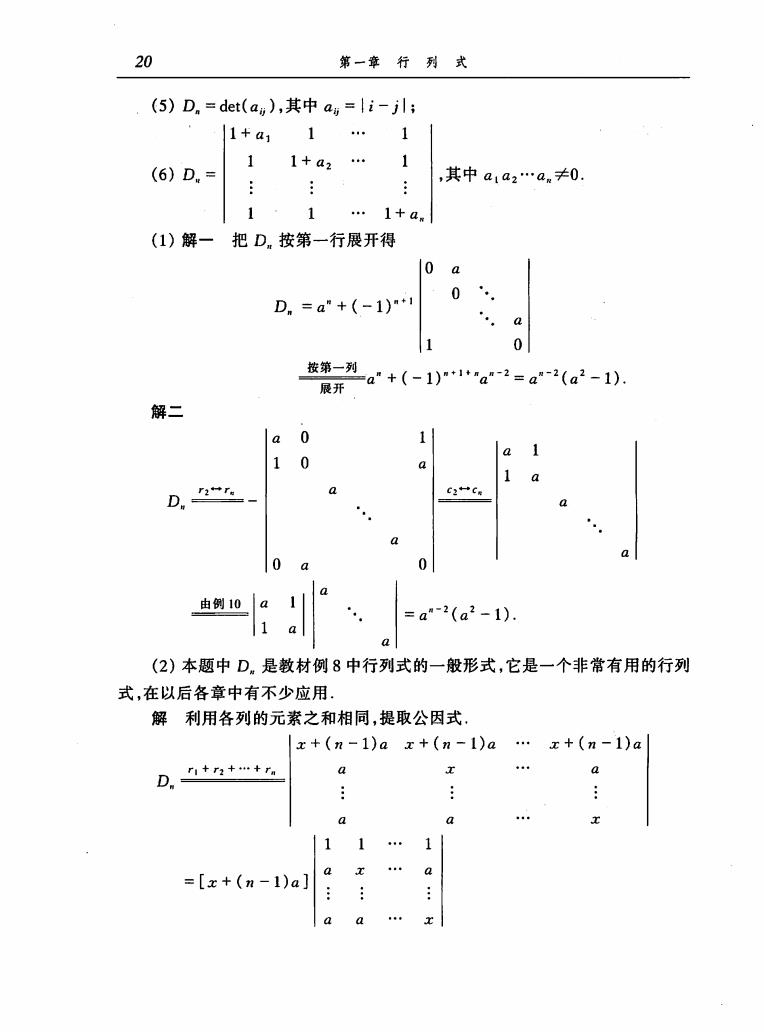
20 第一章行列式 (5)D.=det(a),其中a=li-jl; 1+a11.1 11+a2.1 (6)D.= ,其中a1a2.an≠0 1.1+a (1)解一把D.按第一行展开得 0a 0. D=a"+(-1) ". 0 按第-=列a+(-1)a2=a-2(a2-1) 展开 解二 a 0 1 a 10 D. 0 a 由钢10a1a =a-2(a2-1) 1 a a (2)本题中D。是教材例8中行列式的一般形式,它是一个非常有用的行列 式,在以后各章中有不少应用 解利用各列的元素之和相同,提取公因式 |x+(n-1)ax+(n-1)a.x+(n-1)a D.ntntutn a a a x 11. 1 =[x+(n-1)a]:.a aa.x