
例题制析与增补 11 1 az 1 aj-1 Ay=(-1)1+10 0 0. 0 1 aj+l 按第j-1行展开 -a2.a-1a1+1.a(j=2,3,n) 得 D=a1a,.a,-aaa 4, 注解二毋须a1a2.an≠0的条件. 例1.4利用范德蒙德行列式计算四阶行列式 a +.b d 62 D= 63 d b+c+d a+c+d a+b+d a+b+c a b c d r4+r 解D 1111 把上式等号右边的行列式的最后一行依次与前面的行交换,共交换3次,得 |11141 D=-(a+b+c+d) a b cd a2 b2 c2d2 a'b 此为4阶范德蒙德行列式,根据例12的结果,得 D=-(a+b+c+d)(b-a)(c-a)(d-a)(c-b)(d-b)(d-c). 例1.5计算n+1阶行列式 aia1-1b1a-2b好.b5 D+1= a?-b2 a26号.b2 ab1ab1.b 解首先,我们恒可设a,≠0,i=1,2,.,n+1.因若有某一a,=0,例如

12 第一章行列,式 an+1=0,则将D1按它的第n+1行展开,得到D.+1=b+1D.;若D。中诸a 均不为零,则已如我们之假设;不然,对D,作相同的讨论.其次考察此行列式, 它的第i行元素是a,、b,的n次齐次函数,于是从第i行提取因子a(i=1, 2,+10后,第行第j列元素成为会'G=12.a+1:i=1,2一 n+1),即有 1 . 1 b2 2 D+l=aia.ai+l a2/ a、 1 上式等号右边的行列式为”+1阶范德蒙德行列式之转置行列式,因此 nian总-&) =s及(ab,-ab,). 习题解答 1.利用对角线法则计算下列三阶行列式: 12011 a b c (1)1-4-1; (2)b c a i -183 c a b 111 y x+y (3)a b c (4) y x+y a2 b2 c2 x+y x 解(1)原式=2×(-4)×3+0×(-1)×(-1)+1×1×8 -1×(-4)×(-1)-2×(-1)×8-0×1×3=-4: (2)原式=acb+bac+cba-c3-a3-b3 =3abc-a3-b3-c3; (3)原式=1bc2+1c.a2+1ab2-1ba2-1c.b2-1ac2 bc2+ca2+ab2-ba2-cb2-ac2

习题解答 13 =c2(b-a)+ab(b-a)-c(b2-a2)=(a-b)(b-c)(c-a) (4)原式=x(x+y)y+z(x+y)+(x+y)z-(x+y)3-x3-y3 =-2(x3+y3). 2.按自然数从小到大为标准次序,求下列各排列的逆序数: (1)1234: (2)4132: (3)3421: (4)2413: (5)13.((2n-1)24.(2n); (6)13.(2n-1)(2n)(2n-2).2. 解(1)此排列为自然排列,其逆序数为0: (2)此排列的首位元素的逆序数为0:第2位元素1的逆序数为1:第3位元 素3的逆序数为1;末位元素2的逆序数为2,故它的逆序数为0+1+1+2=4: (3)此排列的前两位元素的逆序数均为0:第3位元素2的逆序数为2:末 位元素1的逆序数为3,故它的逆序数为0+0+2+3=5; (4)类似于上面,此排列的从首位元素到末位元素的逆序数依次为0,0,2, 1,故它的逆序数为0+0+2+1=3: (5)注意到这2n个数的排列中,前n位元素之间没有逆序对.第n+1位 元素2与它前面的n-1个数构成逆序对,故它的逆序数为n-1;同理,第n+2 倍元素4的逆序数为n一2;;末位元素2n的逆序数为0.故此排列的逆序数 为(n-1)+(n-2)+.+0=n(n-1): (6)与(5)相仿,此排列的前n+1位元素没有逆序对:第n+2位元素 (2n-2)的逆序数为2:第n+3位元素2n-4与它前面的2n-3,2n-1,2n 2n-2构成逆序对,故它的逆序为4::末位元素2的逆序数为2(n-1),故此 排列的逆序数为2+4+.+2(n-1)=n(n-1). 3.写出四阶行列式中含有因子a1a3的项 解由行列式定义知这项必还含有分别位于第3行和第4行的某两元素, 而它们又分别位于第2列和第4列,即a2和au或a和a2.注意到排列1324 与1342的逆序数分别为1与2,故此行列式中含有a1aa的项为-a1a23a2a4 与ana23aya2 4.计算下列各行列式: 4124 |2141 1202 (1) (2) 3-121 10520 232 0117 062
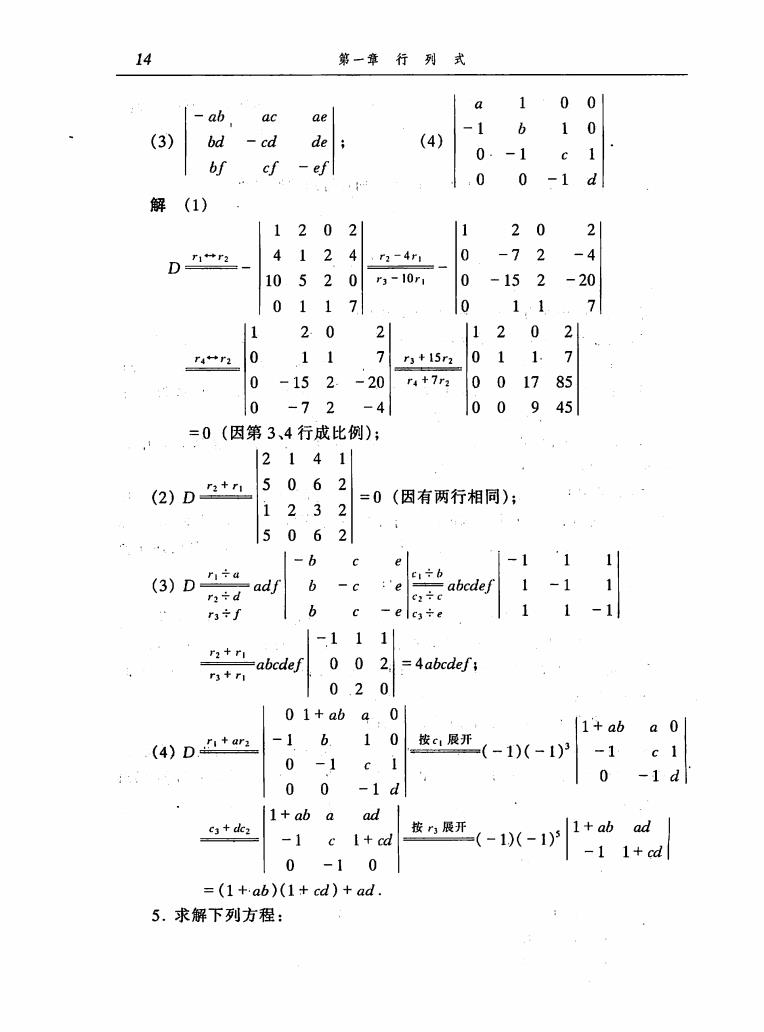
14 第一章行列式 a 1 00 ab ac -1 b 10 (3) -cd de (4) 0 -1 f cf .00-1d 解(1) 1202 1 20 D 4124-41 0 -72 -4 10520r-10r1 0 -152-20 0117 0 11 20 11202 11 7+15r 011.7 0-152-20r4+7r3001785 \0 -72 -4 00945 =0(因第3、4行成比例); |2141 (2)D+ 5062 =0(因有两行相同); 1232 5062 4 1-b c -1 ‘11 (3)D÷a b -c 1 b c-ec,÷e 1 1-1 -111 ntr r3+r -abcdef 00 2.=4abcdef; 0.20 101+ab4.0 :|1+aba0 (4)Dtar2 -1 b 10按展开(-1)(-1 -1c1 0 -1 c I -1d 00 -1d 0 1+ab a ad c3+dez -1 c I+cd n展开(-1-1y1+b, -11+cd 0 -10 =(1+ab)(1+cd)+ad. 5.求解下列方程:

习题解答 15 x+12 -1 11111 (1)2x+1 1 =0:(2) z a b c -11x+1 z2 a2 b2 c2 =0,其中a,b,c z a b c3 互不相等 11 0 解(1)左式 n+x+3)2+11 -11x+1 100 -(x+3)2x-1 1 -12 x+1 =+:-+9r- 于是方程的解为:x1=-3,x2=√3,x,=-√3; (2)注意到方程左式为4阶范德蒙德行列式,由例12的结果得 (x-a)(x-b)(x-c)(a-b)(a-c)(b-c)=0. 因a,b,c互不相等,故方程的解为:x1=a,x2=b,x=c 6.证明: a2 ab 62 (1)2aa+b2b=(a-b)2: 111 ax+by ay+bz ax+bx z y z (2)ay+bz az+bz ax+by =(a'+b)y z: az+br ax+by ay+bz z x y a2(a+1)2(a+2)2(a+3)2 (3) 62(b+1)2(b+2)2(b+3)2 e2(c+1)2(c+22(c+3)2 =0: d2(d+1)2(d+2)2(d+3)2 1111 (4) a b c d a2 b2 c2 d2 a4b4cd° =(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)(a+b+c+d);