
电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 3.1 Background Origin g(x,y)=T[f(x,y)】 (x,y) 3 x 3 neighborhood of(x,y) FIGURE 3.1 A3×3 neighborhood about a point (x,y)in an image in the spatial domain.The neighborhood is moved from pixel Image f to pixel in the image to generate Spatial domain an output image. X
3.1 Background g x y T f x y ( , ) ( , ) =
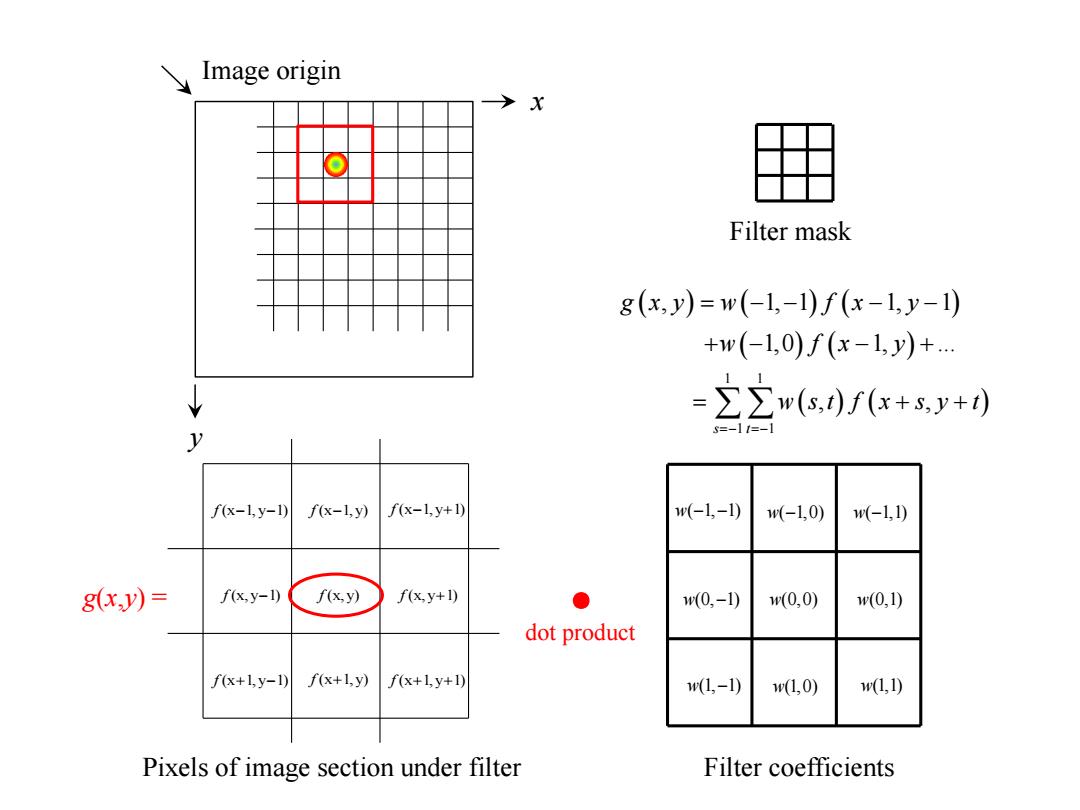
Image origin X Filter mask g(x,y)=w(-1,-1)f(x-1,y-1) +w(-1,0)f(x-1,y)+ =∑(.f(ex+sy+) fx-1,y-1)fx-1,y) f(x-l,y+1) w(-1,-1) w(-1,0) w(-1,1) g(x.y)= f(x,y-1) f(x,y) f(x.y+1) ● w(0,-1) 1w(0,0) w(0,1) dot product f(x+Ly-l)f(x+ly) f(x+1,y+I) w(1,-1) w(L,0) w(L,1) Pixels of image section under filter Filter coefficients
Filter mask w( 1, 1) − − w( 1,0) − w( 1,1) − w(0, 1) − w(0,0) w(0,1) w(1, 1) − w(1,0) w(1,1) Filter coefficients f (x 1, y 1) − − f (x 1, y) − f (x 1, y 1) − + f (x, y 1) − f (x, y) f (x 1, y 1) + − f (x 1, y) + f (x, y 1) + f (x 1, y 1) + + Pixels of image section under filter x y Image origin ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 1 , 1, 1 1, 1 1,0 1, ... , , s t g x y w f x y w f x y w s t f x s y t =− =− = − − − − + − − + = + + ● dot product g(x,y) =
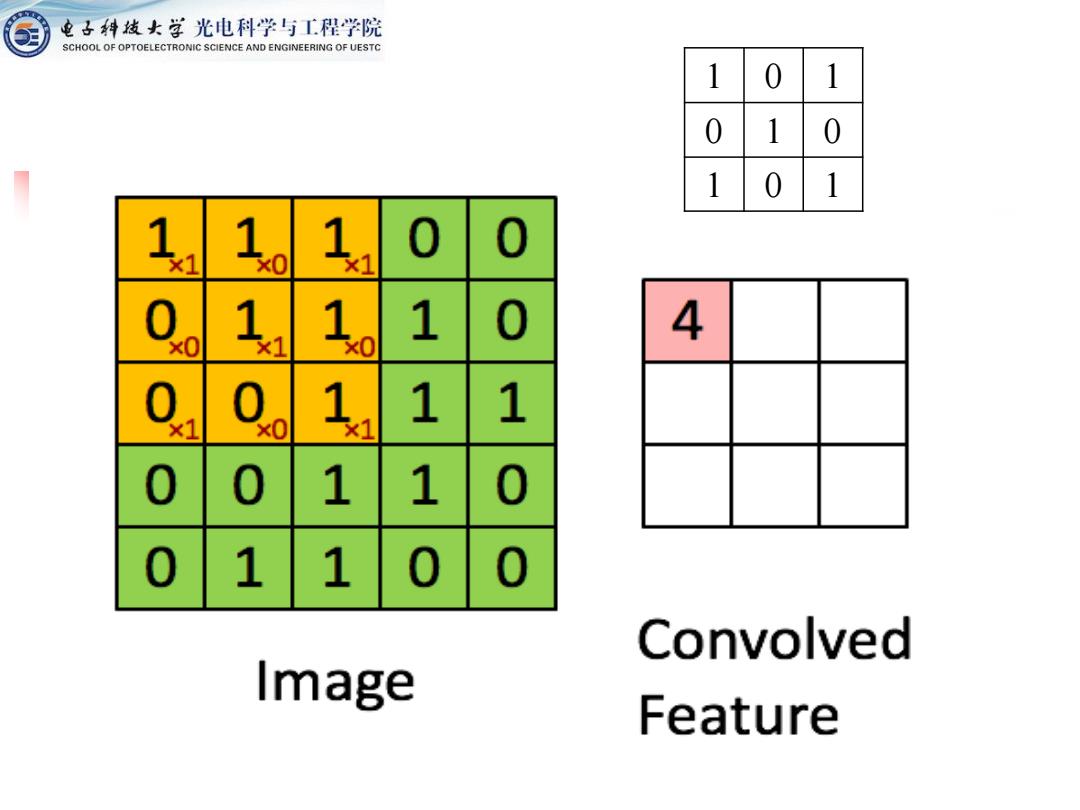
电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 1 0 1 0 1 0 1 0 1 1 11 0 0 0 1 1 0 4 ×1 1 1 1 0 0 1 1 0 1 1 Convolved Image Feature
1 0 1 0 1 0 1 0 1
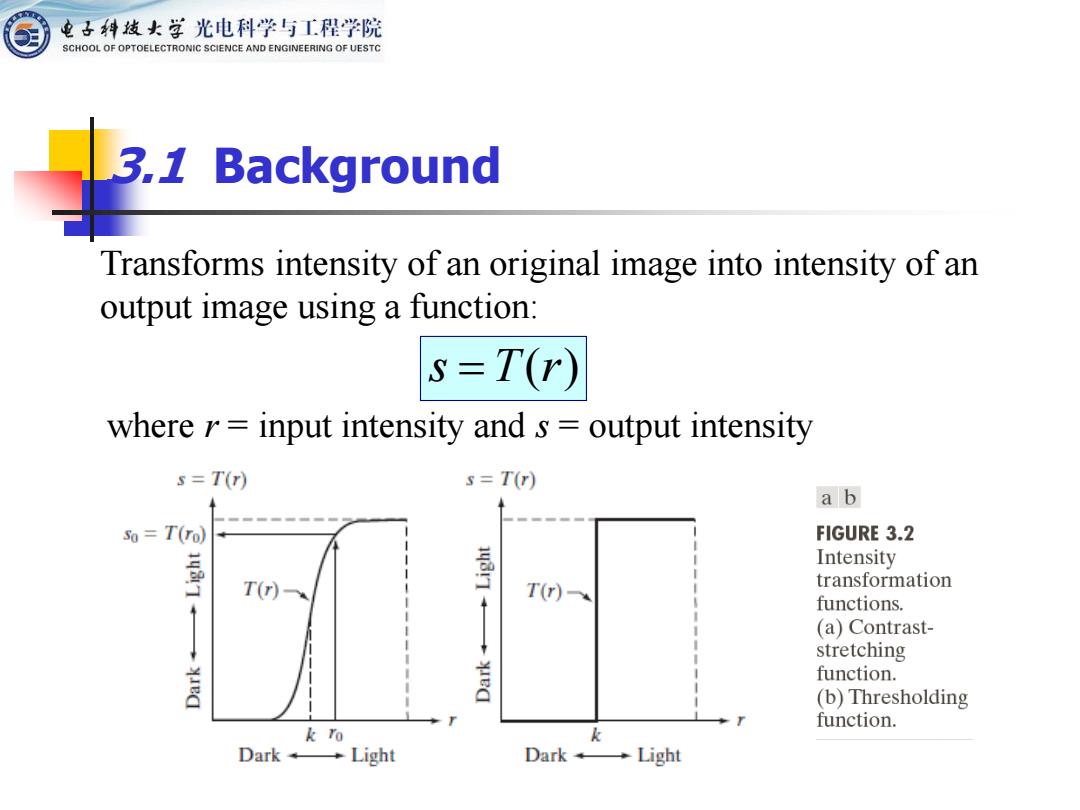
电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 3.1 Background Transforms intensity of an original image into intensity of an output image using a function: s=T(r) where r=input intensity and s output intensity s=T() s=T(r) a b so=T(ro) FIGURE 3.2 1q3 Intensity T(r) T(r) transformation functions. (a)Contrast- stretching yed function. (b)Thresholding function. k ro k Dark→Light Dark→Light
Transforms intensity of an original image into intensity of an output image using a function: s T r = ( ) where r = input intensity and s = output intensity 3.1 Background

电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Outline ◆Background Some Basic Intensity Transformation Functions ◆ Histogram Processing ◆ Fundamentals of Spatial Filtering Smoothing Spatial Filters Sharpening Spatial Filters ◆ Combining Spatial Enhancement Methods Using Fuzzy Techniques
Outline ◆ Background ◆ Some Basic Intensity Transformation Functions ◆ Histogram Processing ◆ Fundamentals of Spatial Filtering ◆ Smoothing Spatial Filters ◆ Sharpening Spatial Filters ◆ Combining Spatial Enhancement Methods ◆ Using Fuzzy Techniques *