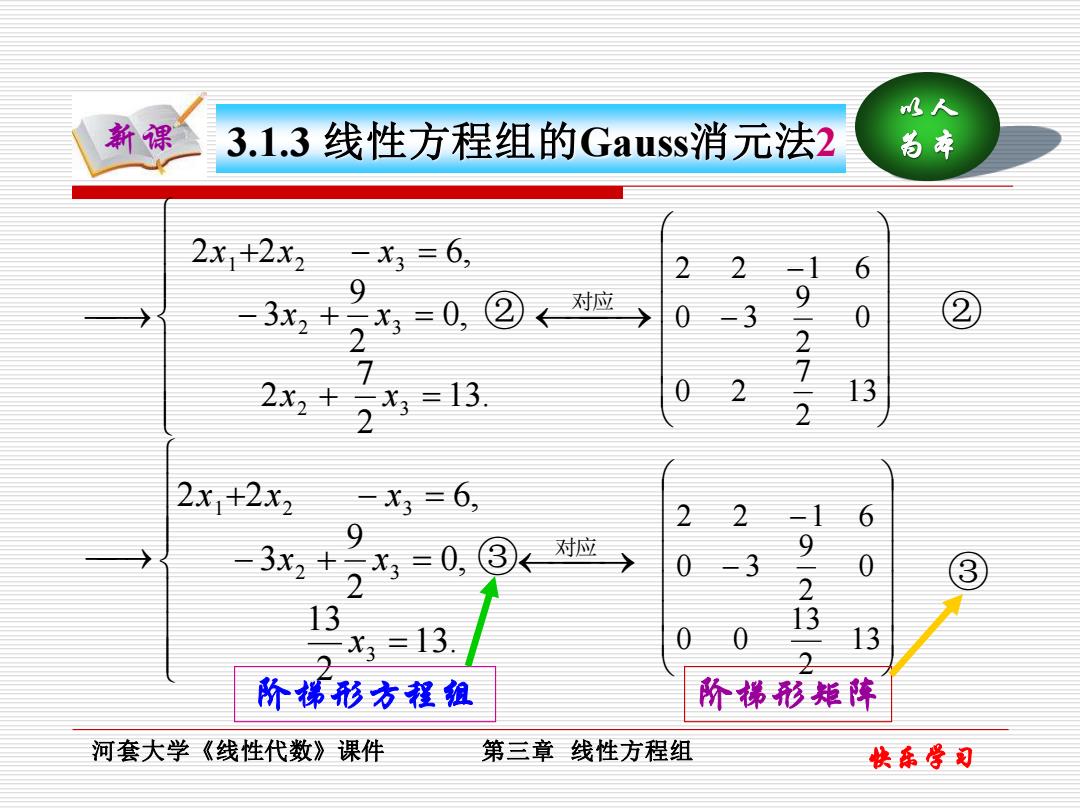
水人 新课 3.1.3线性方程组的Gauss消元法2 尚本 2x1+2x2-x3=6, 2 2 6 对应 9 3x2+x3=0, 0 -3 0 2 27 2x2+ 213 2 13 2 2x1+2x2 -=X3=6, 2 2 6 9 3+=0® 对应 9 0 -3 0 2 13 3=13 0 13 阶梯形方程组 阶梯形矩阵 河套大学《线性代数》课件 第三章线性方程组 快东学司
快乐学习 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 3.1.3 线性方程组的Gauss消元法2 + = − + = + − = 13. 2 7 2 0, 2 9 3 2 2 6, 2 3 2 3 1 2 3 x x x x x x x 对应 ⎯→ − − 13 2 7 0 2 0 2 9 0 3 2 2 1 6 = − + = + − = 13. 2 13 0, 2 9 3 2 2 6, 3 2 3 1 2 3 x x x x x x 对应 ⎯→ ② ② ③ − − 13 2 13 0 0 0 2 9 0 3 2 2 1 6 ③ ⎯→ ⎯→ 阶梯形方程组 阶梯形矩阵

水人 新课 3.1.3线性方程组的Gauss消元法3 尚本 2x1+2x2-X3=6, 2 2 6 9 3x,+2=0 4 对应 0 -3 4 X3=2 2x1+2x2 =8, 220 8 ⑤ 对应 -3x2 =-9 0 -30 ¥3=2 阶梯形方程组 阶梯形矩阵 河套大学《线性代数》课件 第三章线性方程组 快东学司
快乐学习 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 3.1.3 线性方程组的Gauss消元法3 ⎯→ = − + = + − = 2. 0, 2 9 3 2 2 6, 3 2 3 1 2 3 x x x x x x 对应 ⎯→ − − 0 0 1 2 0 2 9 0 3 2 2 1 6 ④ ④ ⎯→ = − = − + = 2. 3 9, 2 2 8, 3 2 1 2 x x x x 对应 ⎯→ − − 0 0 1 2 0 3 0 9 2 2 0 8 ⑤ ⑤ 阶梯形方程组 阶梯形矩阵

水人 新课 3.1.3线性方程组的Gauss消元法4 尚本 2x1+2X2 =8, 2 2 8 X2 =3, ⑥ 对应 ¥3=2 2X1 =2, 对应 X2 =3, X3=2 阶梯形大程组 阶梯形矩阵 河套大学《线性代数》课件 第三章线性方程组 快东学司
快乐学习 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 3.1.3 线性方程组的Gauss消元法4 ⎯→ = = + = 2. 3, 2 2 8, 3 2 1 2 x x x x 对应 ⎯→ 0 0 1 2 0 1 0 3 2 2 0 8 ⎯→ = = = 2. 3, 2 2, 3 2 1 x x x 对应 ⎯→ 0 0 1 2 0 1 0 3 2 0 0 2 ⑥ ⑥ ⑦ ⑦ 阶梯形方程组 阶梯形矩阵
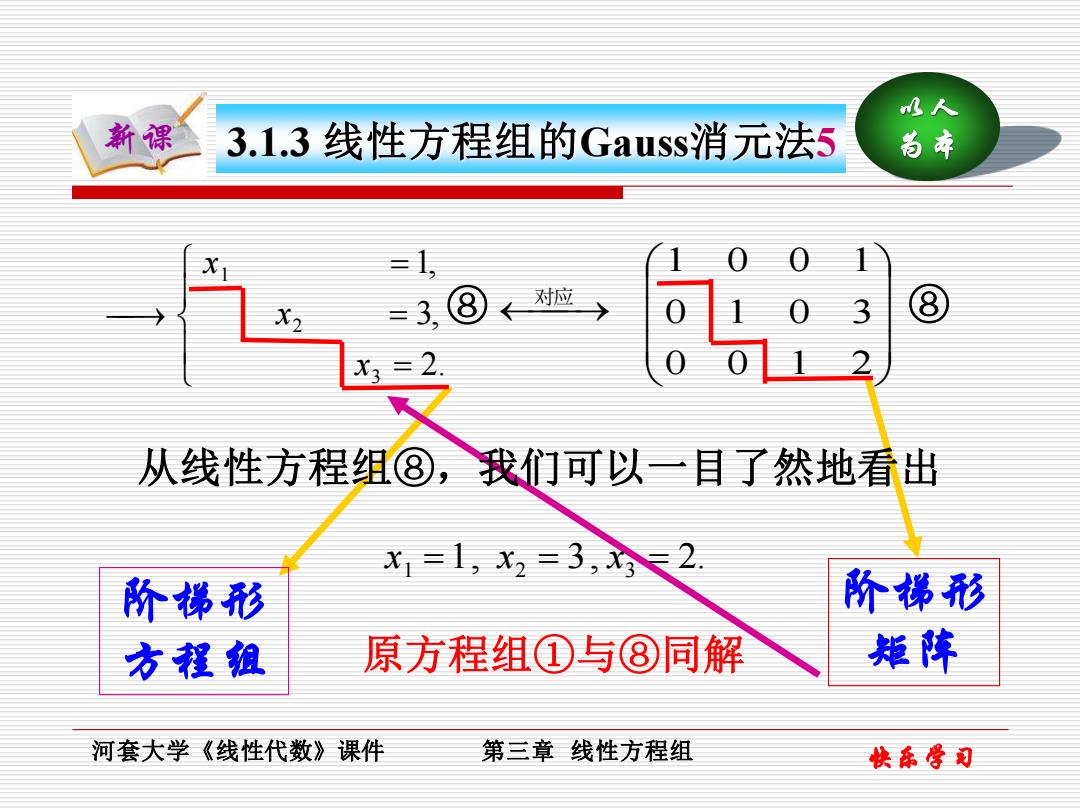
水人 新课 3.1.3线性方程组的Gauss:消元法5 尚本 =3, 对应 X2 8 =2 从线性方程组⑧,我们可以一耳了然地看出 x1=1,x2=3,3≤2 阶梯形 阶梯形 方程组 原方程组①与⑧同解 矩阵 河套大学《线性代数》课件 第三章线性方程组 快乐学司
快乐学习 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 3.1.3 线性方程组的Gauss消元法5 ⎯→ = = = 2. 3, 1, 3 2 1 x x x 对应 ⎯→ 0 0 1 2 0 1 0 3 1 0 0 1 1, 3, 2. x1 = x2 = x3 = ⑧ 从线性方程组⑧,我们可以一目了然地看出 ⑧ 阶梯形 方程组 阶梯形 原方程组①与⑧同解 矩阵

水人 新课 3.1.3线性方程组的Gauss:消元法6 尚本 在第二章我们给出线性方程组的初等变换的概 念,引出了矩阵的初等变换的概念在第二章还给 出了阶梯形矩阵的概念,当然也对应有阶梯形方 程组的概念.从上述引例可以看出:消元法的目的 就是利用方程组的初等变换将原方程组化为阶梯 形方程组,显然这个梯形方程组与原线性方程 组同解,解这个阶梯形方程组得到原方程组的解 如果用矩阵表示其系数和常数项,则将原方程组 河套大学《线性代数》课件 第三章线性方程组 快乐骨司
快乐学习 以人 新课 为本 河套大学《线性代数》课件 第三章 线性方程组 3.1.3 线性方程组的Gauss消元法6 在第二章我们给出线性方程组的初等变换的概 念,引出了矩阵的初等变换的概念.在第二章还给 出了阶梯形矩阵的概念,当然也对应有阶梯形方 程组的概念.从上述引例可以看出:消元法的目的 就是利用方程组的初等变换将原方程组化为阶梯 形方程组,显然这个阶梯形方程组与原线性方程 组同解,解这个阶梯形方程组得到原方程组的解. 如果用矩阵表示其系数和常数项,则将原方程组