生物统计Chap.6Analysis of VarianceI数学模型Xi随机误差=μu+a+eiZa=0a,=μ-μ,处理i的效应总平均观察值·线性模型:影响观察值的因素效应可加随机误差一随机变量eij:-ej服从正态分布N(0,α2)→Zeij一0,处理所代表的各个总体是同质的不同的e:间是相互独立的=个体之间是独立的
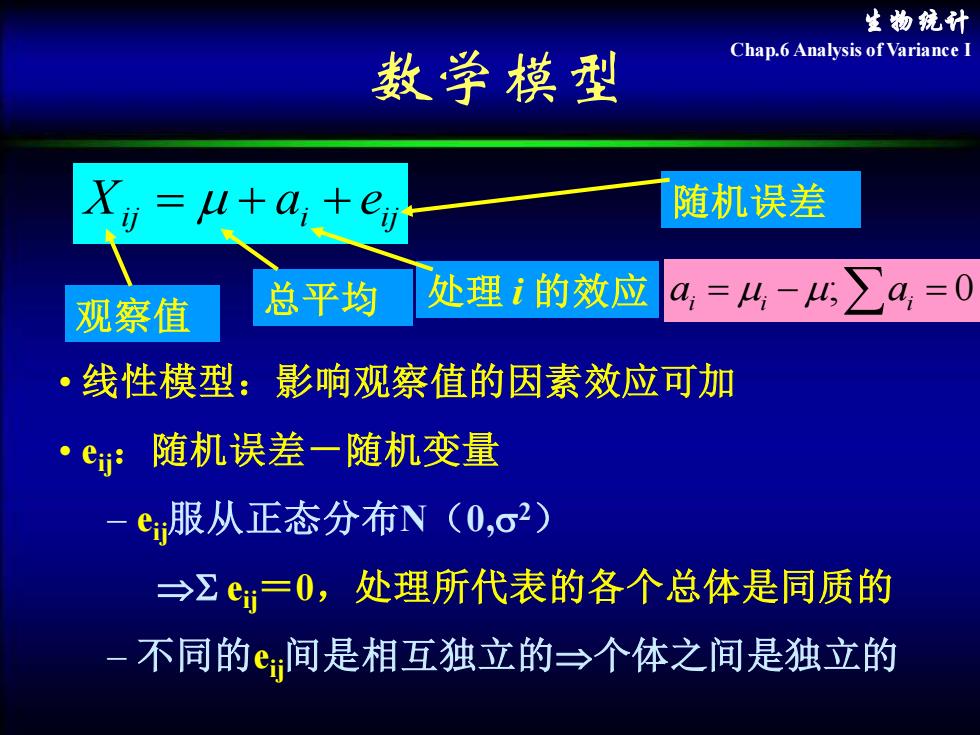
生物统计 Chap.6 Analysis of Variance I 数学模型 ij i ij X = + a + e 总平均 处理 i 的效应 随机误差 观察值 • 线性模型:影响观察值的因素效应可加 • eij:随机误差-随机变量 – eij服从正态分布N(0,2) eij=0,处理所代表的各个总体是同质的 – 不同的eij间是相互独立的个体之间是独立的 ai = i − ;ai = 0
生物统计Chap.6Analvsis ofVariance1单向分类资料的数据结构组别合计平均观测值AXi, ... XX"XXu Xi2:.:X-XnA...X...XX21 X22 ...2j2n2-..X,:XXX,X,...X,in;..XXX7NXX
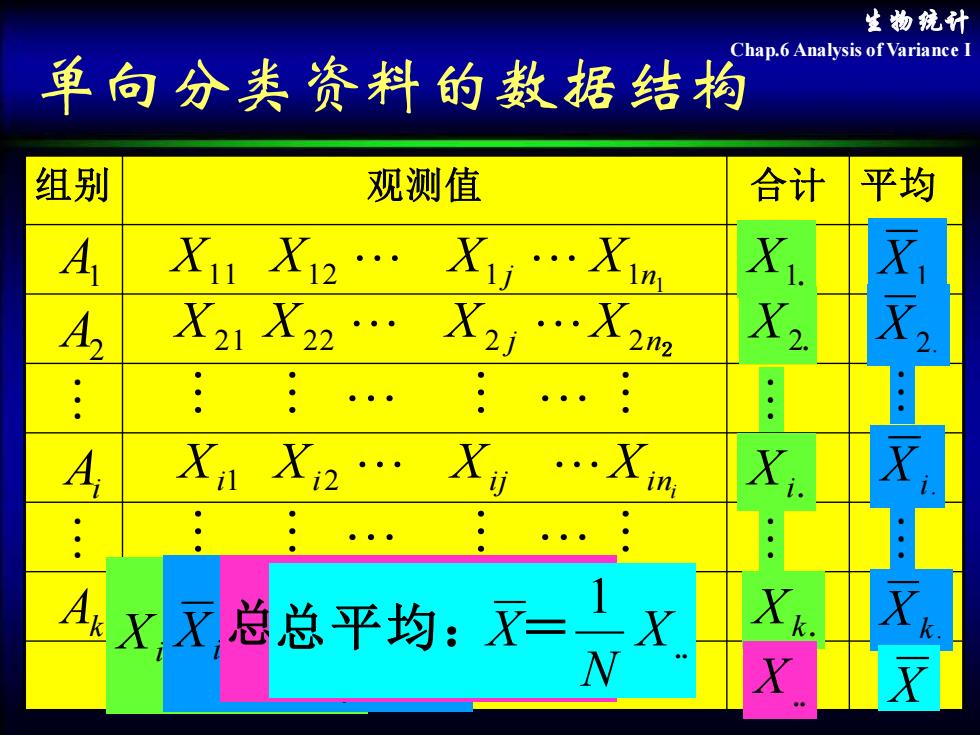
生物统计 Chap.6 Analysis of Variance I 单向分类资料的数据结构 组别 观测值 合计 平均 A1 A2 Ak Ai X1. X2. Xk . Xi. X1. X2. Xk. Xi. 1 1 1 2 1 1n1 X X X j X j n 2 X2 1 X2 2 X2 X2 k Xk1 Xk 2 Xkj Xkn i Xi1 Xi2 Xi j Xi n X . X = = ni j Xi Xij 1 . = = ni j ij i i X n X 1 1 = k i X Xi 1 总和: . = . X. N X 1 总平均: =

生物统计Chap.6Analysis of Variance1平方和与自由度的计算[x,-}]-(x)-总平方和:SSr=i=l j=li=l j=l校正项(correctionfactor):CF(x-)}-()组间平方和:SSCFi=-l= SS-SS2n(X,-X)组间平方和:SS=i==k-1dff =N-1af=N-k=df--df
生物统计 Chap.6 Analysis of Variance I 平方和与自由度的计算 dfT = N −1 dfA = k −1 E dfT dfA df = N −k = − ( ) ( ) N X SS X X X k i n j i j k i n j T i j i i 2 1 1 2 1 1 2 . = − = − = = = = 总平方和: N X correction factor CF 2 . 校正项( ): = ( ) CF n X n X X k i i i k i i i − − = = =1 2 1 2 SSA . . 组间平方和: = ( ) SSE = SST − SSA = = − k i ni Xi X 1 2 SSA . 组间平方和:

生物统计Chap.6Analysis of VarianceI实例一小鼠脾脏2389456nsumgroupaverage15.832586375r80982327119.814.341-72235889.20352012.74859104.260264011.884.7010.599h32398.1012.44398.124952.6128F32C(x2)-YM(12.32 +13.22 +...+11.52)-CF5086.01-CF=133.3972-89.22104.42119.8284.72(兰)-CF=CFSS+XXA88?O=5038.4691-CF=85.8563
生物统计 Chap.6 Analysis of Variance I 实例-小鼠脾脏 4952.6128 32 398.1 2 2 . = = = N X CF group 1 2 3 4 5 6 7 8 9 n sum average I 12.3 13.2 13.7 15.2 15.4 15.8 16.9 17.3 8 119.80 14.98 II 10.8 11.6 12.3 12.7 13.5 13.5 14.8 7 89.20 12.74 III 9.3 10.3 11.1 11.7 11.7 12.0 12.3 12.4 13.6 9 104.40 11.60 I V 9.5 10.3 10.5 10.5 10.5 10.9 11.0 11.5 8 84.70 10.59 3 2 398.10 12.44 ( ) ( ) 5086.01 133.3972 12.3 13.2 11.5 2 2 2 2 . 1 1 2 = − = = − = + + + − = = C F C F N X SS X k i n j T i j j 5038 4691 85 8563 8 84 7 9 104 4 7 89 2 8 119 8 2 2 2 2 1 2 A . . . . . . . = − = − − = + + + = CF CF CF n X SS k i i = i
生物统计Chap.6AnalysisofVarianceI实例一小鼠脾脏23546891-sumgroupaverage28315327556119.88014.98372889.2012.74-960104.4011.6884.7010.5993212.44398.10S=SS-SS,=133.3971-85.8563=47.5408S= N-1=32-1=31=k-1=4-1=E=N-k=32-4=28定义统计量三均方(meansquare,MS)=平方和/自由度47.540985.8563MS=1.6979=16.855,MSA328
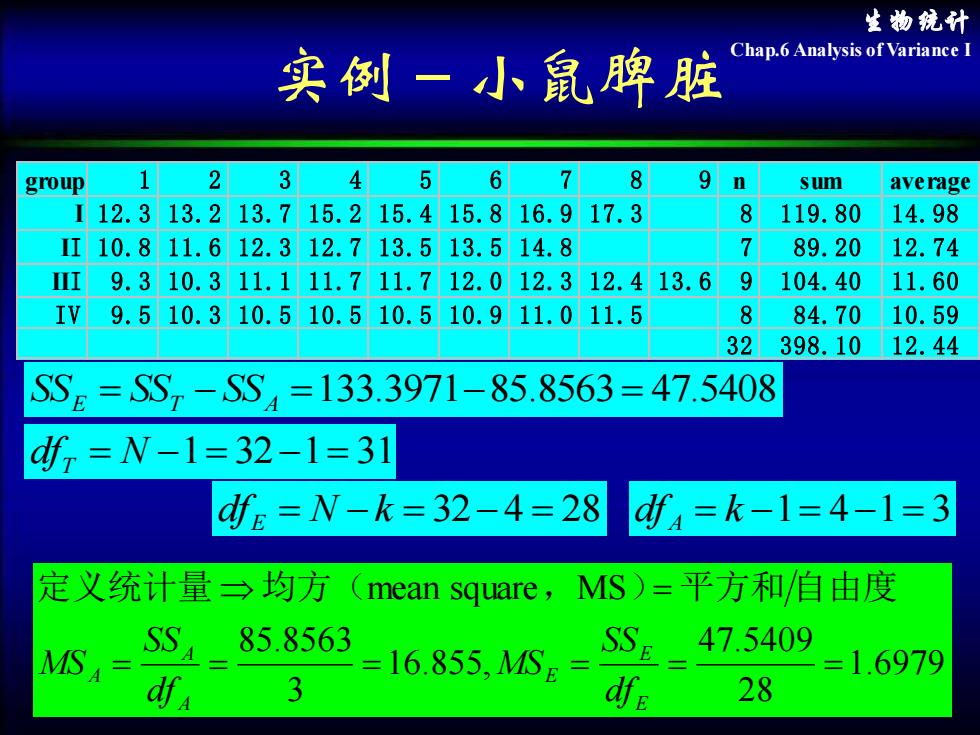
生物统计 Chap.6 Analysis of Variance I 实例-小鼠脾脏 group 1 2 3 4 5 6 7 8 9 n sum average I 12.3 13.2 13.7 15.2 15.4 15.8 16.9 17.3 8 119.80 14.98 II 10.8 11.6 12.3 12.7 13.5 13.5 14.8 7 89.20 12.74 III 9.3 10.3 11.1 11.7 11.7 12.0 12.3 12.4 13.6 9 104.40 11.60 I V 9.5 10.3 10.5 10.5 10.5 10.9 11.0 11.5 8 84.70 10.59 3 2 398.10 12.44 dfT = N −1= 32−1= 31 dfE = N −k = 32−4 = 28 dfA = k −1= 4−1= 3 1.6979 28 47.5409 16.855, 3 85.8563 mean square MS = = = = = = = E E E A A A df SS MS df SS MS 定义统计量 均方( , ) 平方和 自由度 SSE = SST − SSA =133.3971−85.8563 = 47.5408