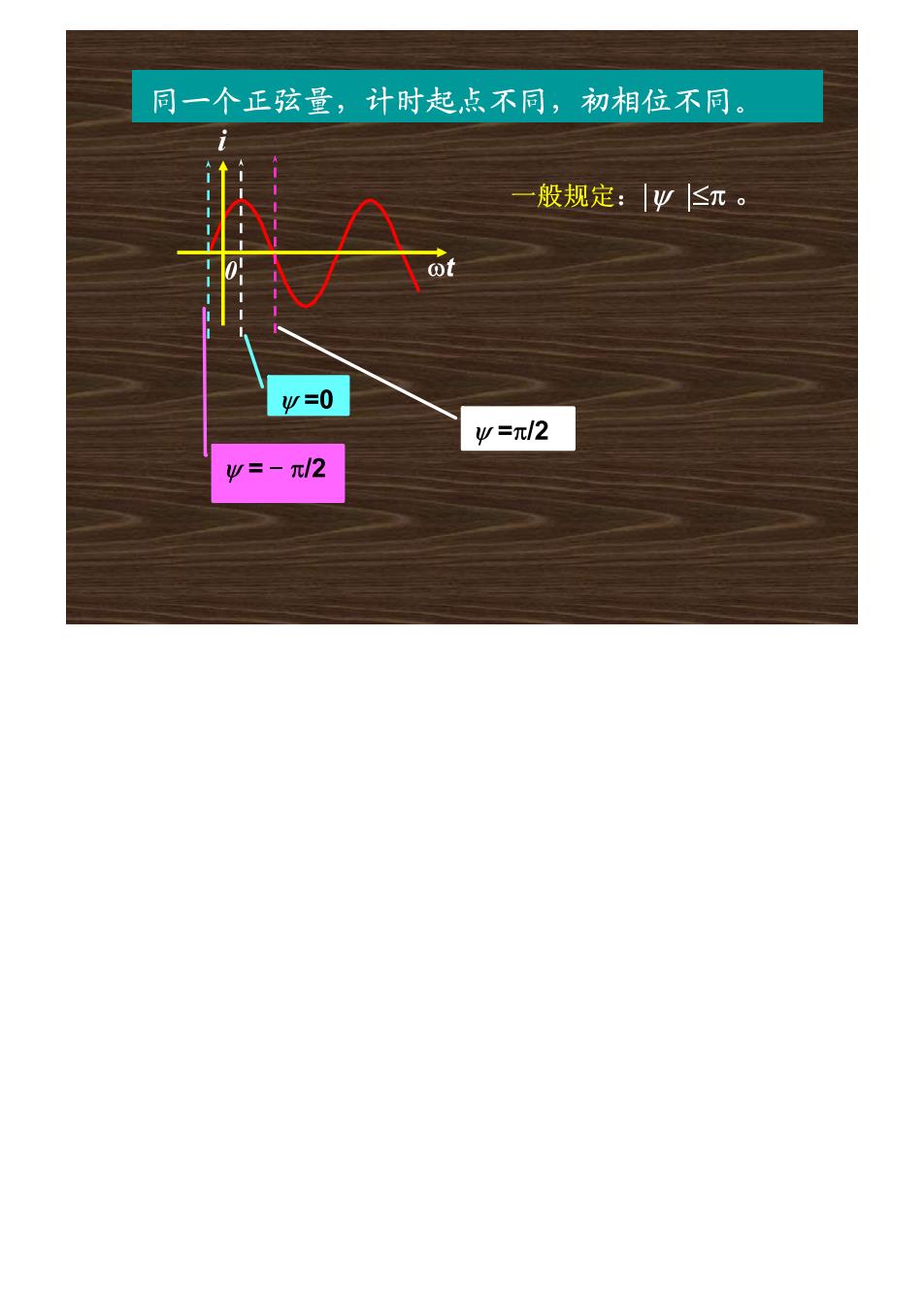
同一个正弦量,计时起点不同,初相位不同。 A 般规定:V≤π。 业=0 y=π/2 y=-π/2
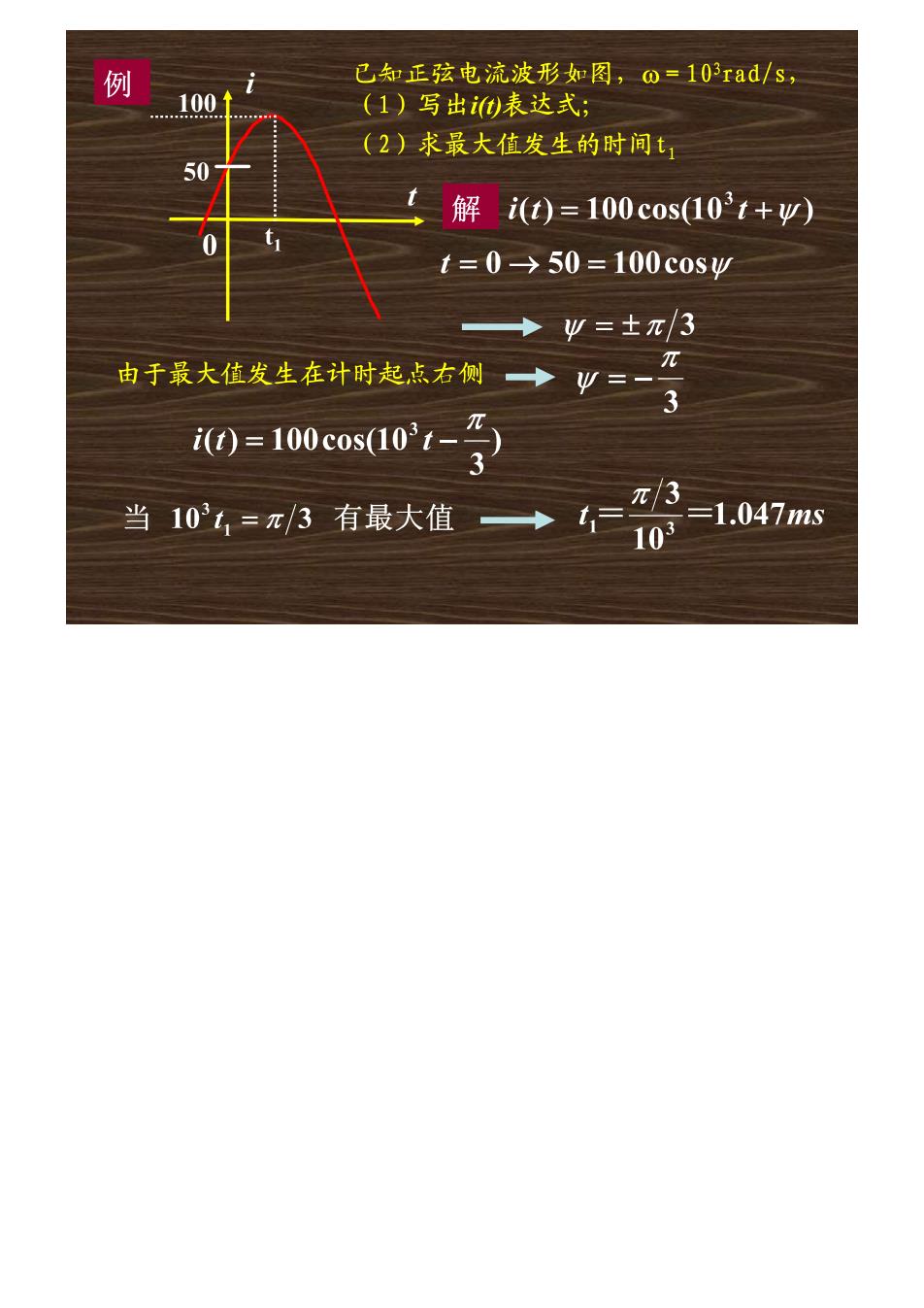
例 已知正弦电流波形如图,o=103rad/s, 100 (1)写出0表达式 (2)求最大值发生的时间t 50 解 it)=100c0s(103t+w) t t=0→50=100c0sW ◆w=士元/3 由于最大值发生在计时起点右侧→ π W=- 3 0)=10cas01-7 当103t,=π/3有最大值 → π/3 103 =1.047s
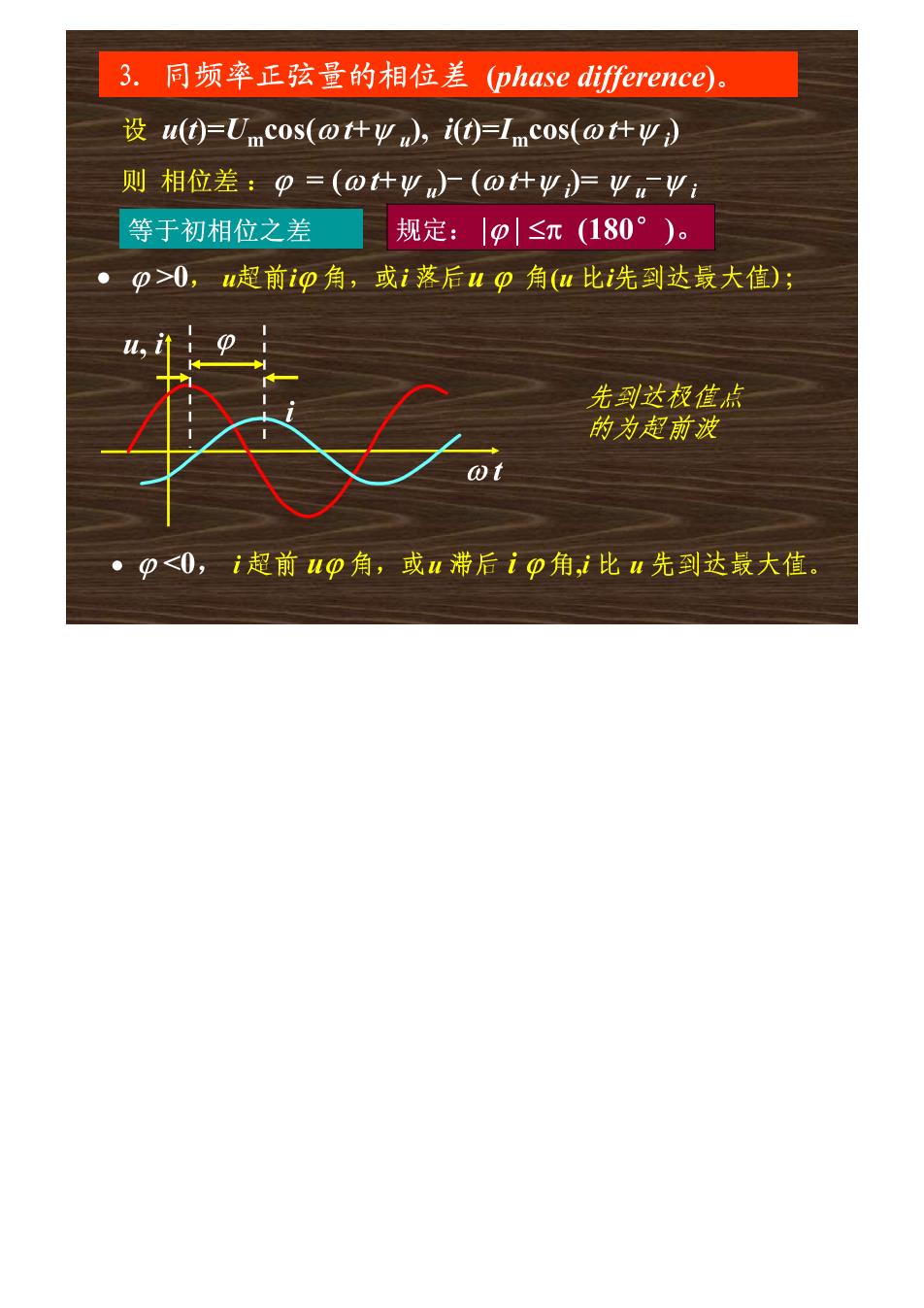
3. 同频率正弦量的相位差(phase difference)。 设u()=Umc0s(ot什y),it)=Imcos(o什Ψ) 则相位差:p=(o什Ψ)广(o什Ψ)卢V业 等于初相位之差 规定:|p|≤元(180°)。 ● p>0,u超前ip角,或i落后up角(u比i先到达最大值); 先到达极值点 的为超前波 ● 0<0,i超前up角,或u滞后ip角,i比u先到达最大值

特殊相位关系: 0=±元(仕180°),反相: u, 0三0,同相: u, 0=π/2: u领先i元/2,不说u落后i3元/2; i落后uπ/2,不说i领先u3π/2。 同样可比较两个电压或两个电流的相位差

例 计算下列两正弦量的相位差。 解 1) i(t)=10c0s(100πt+3π4) 0=3π/4-(-π/2)=5π/4>元 i,(t)=10c0s(100πt-π/2) ◆p=2π-5π/4=3π/4 (2)()=10c0s(100元t+30)i2(t)=10c0s(100m-105) i,(t)=10sin(100πt-15) p=30°-(-105=1350 (3)4(t)=10c0s(100πt+30°) ⊙1丰02 u2(t)=10c0s(200mt+450) 不能比较相位差 (4)i,(0=5c0s(100mt-30) i2(t)=3c0s(100m-150) i2(t)=-3c0s(100mt+30)7p=-30°-(-150=120° 两个正弦量进行相位比较时应满足同频率、同函数、同符 号,且在主值范围比较