中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 8.1 Euler公式 做等距分割,利用数值微分代替导数项,建立差分方程。 b-ai 称为局部截断 m 误差。显然, 1、向前差商公式 这个误差在逐 -y)+y() 步计算过程中 h 会传播,积累。 区)=fxx》+2"(5.) 因此还要估计 h 这种积累 y(x)=y(x)+hf(xn2 y(x))+ 2(5 所以,可以构造差分方程 ynti=yn+hf(xn2 yn)
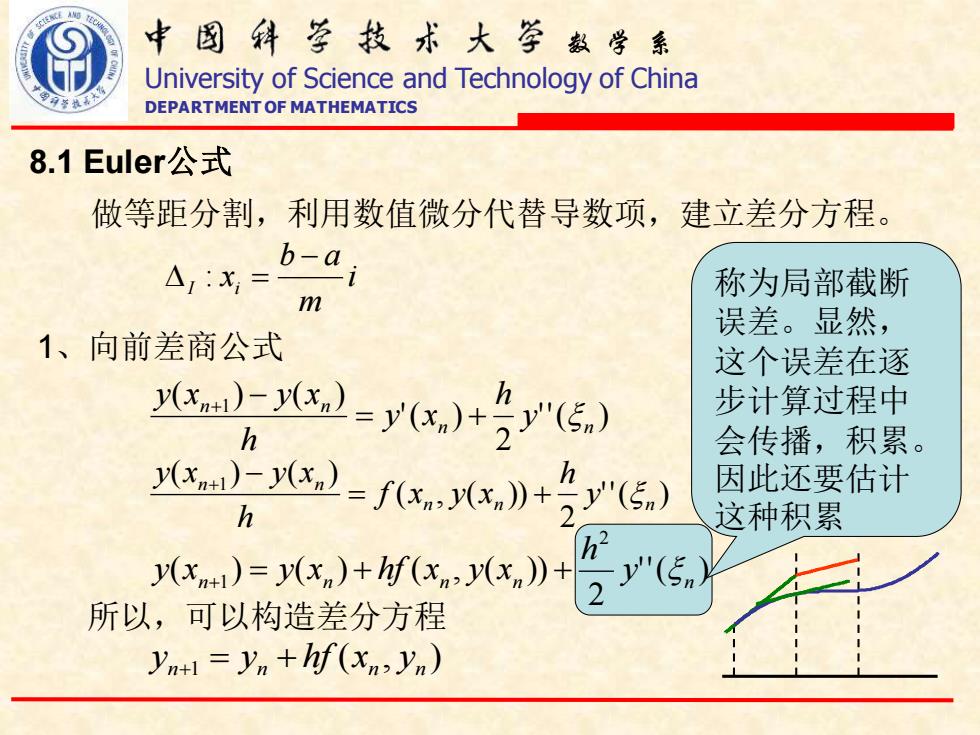
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 8.1 Euler公式 做等距分割,利用数值微分代替导数项,建立差分方程。 i m b a x I i − : = 1、向前差商公式 ''( ) 2 '( ) ( ) ( ) 1 n n n n y h y x h y x y x = + + − ''( ) 2 ( , ( )) ( ) ( ) 1 n n n n n y h f x y x h y x y x = + + − ''( ) 2 ( ) ( ) ( , ( )) 2 n 1 n n n n y h y x + = y x + hf x y x + 所以,可以构造差分方程 ( , ) n 1 n n n y = y + hf x y + 称为局部截断 误差。显然, 这个误差在逐 步计算过程中 会传播,积累。 因此还要估计 这种积累

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 定义在假设,=yx),即第i步计算是精确的前提下,考虑 的截断误差R;=y化#)-y+1称为局部截断误差*local truncation error*l。 定义若某算法的局部截断误差为O(+),则称该算法有p阶 精度。 2、收敛性 考察局部误差的传播和积累 y(x)=y(x)+hf(x2 y(x))+ 2y"(5) ynti =yn+hf(xn2yn) 记为hTm+
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 定义 在假设 yi = y(xi ),即第 i 步计算是精确的前提下,考虑 的截断误差 Ri = y(xi+1 ) − yi+1 称为局部截断误差 /* local truncation error */。 定义 若某算法的局部截断误差为O(h p+1 ),则称该算法有p 阶 精度。 记为 2、收敛性 ''( ) 2 ( ) ( ) ( , ( )) 2 n 1 n n n n y h y x + = y x + hf x y x + ( , ) n 1 n n n y = y + hf x y + hTn+1 考察局部误差的传播和积累

中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS e=y(x)-y ≤y(xn)-ynl+hf(xn,(xn》-f(xa,yn+hATl ≤en+hLy(xn)-yn+hTl ≤(1+hL)len+hT,T=maxT, ≤1+h)1+hL)en+hT)+h7 =(1+hL)2en+(1+hL)+1)hT ≤(1+hL)2《1+hL)len-2+hT)+(+hL)+1h7 =(1+hL)em-2+(1+hL)2+(1+hL)+1h7 ≤
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 1 1 1 ( ) n+ = n+ − n+ e y x y 1 ( ) ( , ( )) ( , ) n − n + n n − n n + hTn+ y x y h f x y x f x y 1 ( ) n + n − n + hTn+ e hL y x y j j (1+ hL) en + hT , T = max T (1+ hL)((1+ hL) en−1 + hT)+ hT (1 hL) en 1 ((1 hL) 1)hT 2 = + − + + + (1 hL) ((1 hL) en 2 hT) ((1 hL) 1)hT 2 + + − + + + + (1 hL) en ((1 hL) (1 hL) 1)hT 2 2 3 = + − + + + + +
中图科学技术大空数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS ≤(I+hL)mel+(1+hL)”++(1+hL)+1hT =0+rs,+二0+"A 1-(1+hL) s1+L+0+)h7 sd-m) e=0 (1+x)”<em T=O(h) e+1=O(h) 是1阶 称为整体截断误差 方法
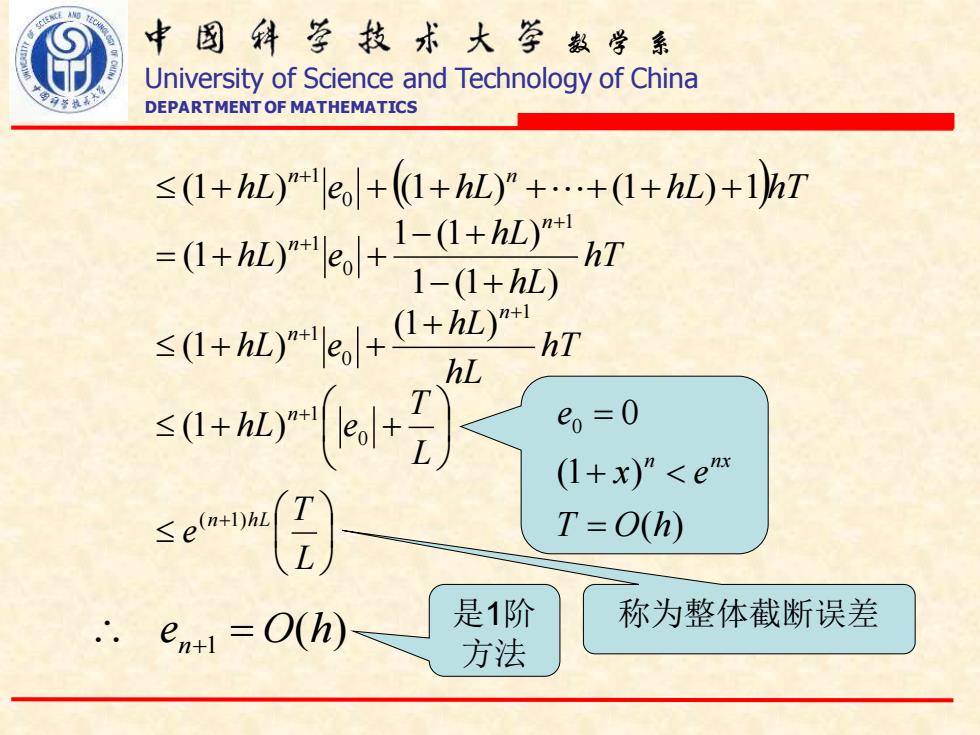
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS hL e ( hL hL )hT n n (1 ) 0 (1 ) (1 ) 1 1 + + + + + + + + hT hL hL hL e n n 1 (1 ) 1 (1 ) (1 ) 1 0 1 − + − + = + + + + hT hL hL hL e n n 1 0 1 (1 ) (1 ) + + + + + + + + L T hL e n 0 1 (1 ) + L T e (n 1)hL ( ) en+1 = O h ( ) (1 ) 0 0 T O h x e e n nx = + = 是1阶 称为整体截断误差 方法

中固斜亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 3、稳定性一误差在以后各步的计算中不会无限制扩大。 我们考虑简单情况:仅初值有误差,而其他计算步骤无误差。 设{z,}是初值有误差后的计算值,则 yn+=yn+hf(xn2yn) Ent1=2n+hf(Xn 2n) 所以,我们有: e+i=yn+1-2n+i≤len+hAf(xn,yn)-f(xn,zn)》 e,+hly,-z,=en(1+hL) ≤.≤lell+hL)m1≤eem+hl 可以看出,向前差商公式关于初值是稳定的。当初始误差 充分小,以后各步的误差也充分小
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 3、稳定性-误差在以后各步的计算中不会无限制扩大。 我们考虑简单情况:仅初值有误差,而其他计算步骤无误差。 设 { }i z 是初值有误差后的计算值,则 ( , ) ( , ) 1 1 n n n n n n n n z z hf x z y y hf x y = + = + + + 所以,我们有: ( , ) ( , ) n 1 n 1 n 1 n n n n n e y − z e + h f x y − f x z + + + e hL y z e (1 hL) n + n − n = n + n n hL e hL e e ( 1) 0 1 0 (1 ) + + + 可以看出,向前差商公式关于初值是稳定的。当初始误差 充分小,以后各步的误差也充分小