
例1:零输入响应电路求解 3k2 例1图示电路原处于 十 稳态,=0时将开 关接到“2”,对≥0 18 求uc uc(0)=18×6/9=12V uc(0+)=uc(0)=12V 解法一:从建立电路的方程入手 106+双+0=0 3k2 1F÷ 6k2 dc+500uc-0 dt (t>0) uc=ke-500t uc=12e-500t (≥0)
+ - 18v 1PF 6k: uc 3k: + - ֻ1 മ⽪⭥䐟༴Ҿ っᘱˈt=0ᰦሶᔰ ޣ᧕ࡠ”2”ˈሩtt0 ≲uCDŽ 1 2 uC(0– )=18u6/9=12V uC(0+ )= uC(0– ) =12V 10–6 duC dt 3u103 uC 6u103 uC + + =0 duC dt + 500uC =0 uC=ke–500t uC=12e–500t (tt0) 1PF 6k: uc 3k: + - (t > 0) 䀓⌅а˖Ӿᔪ・⭥䐟Ⲵᯩ〻ޕ ֻ1˖䴦䗃ޕ૽ᓄ⭥䐟≲䀓
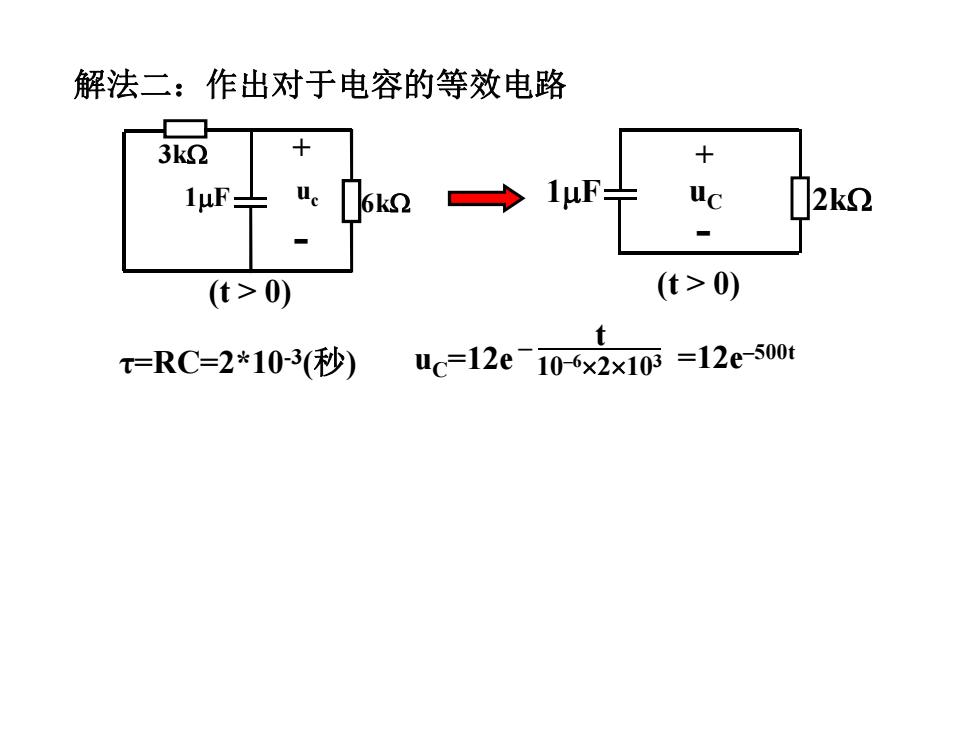
解法二:作出对于电容的等效电路 3k2 十 2k2 (t>0) (t>0) t T=RC=2*103(秒) uc=12e-10-6x2x10=12e-500t
1PF 6k: uc 3k: + - (t > 0) 䀓⌅Ҽ˖ࠪሩҾ⭥ᇩⲴㅹ᭸⭥䐟 1PF uC 2k: + - (t > 0) uC=12e – 10–6u2u103 t =12e–500t IJ=RC=2*10-3(。)
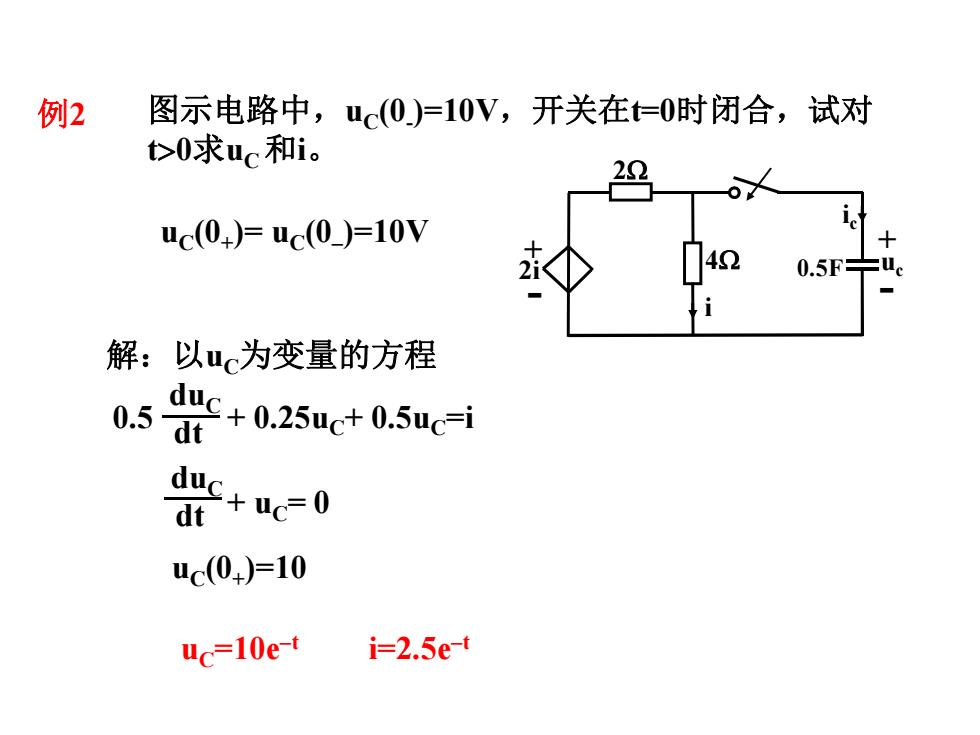
例2 图示电路中,c(0)=10V,开关在=0时闭合,试对 t>0求uc和i 2 uc(0+)=c(0)=10V 4 0.5F+ 解:以u为变量的方程 d业c+0.25c+0.5ue-i 0.5 c+uc=0 dt uc(0)=10 uc=10e-t i=2.5e-t
䀓˖ԕuCѪਈ䟿Ⲵᯩ〻 0.5 + 0.25uC+ 0.5uC=i duC dt + uC= 0 duC dt uC(0+ )=10 uC=10e–t i=2.5e–t ֻ2 + - 4: 0.5F uc 2: + - 2i i i c മ⽪⭥䐟ѝˈuC(0- )=10Vˈᔰޣ൘t=0ᰦ䰝ਸˈ䈅ሩ t!0≲uC ઼iDŽ uC(0+ )= uC(0– )=10V
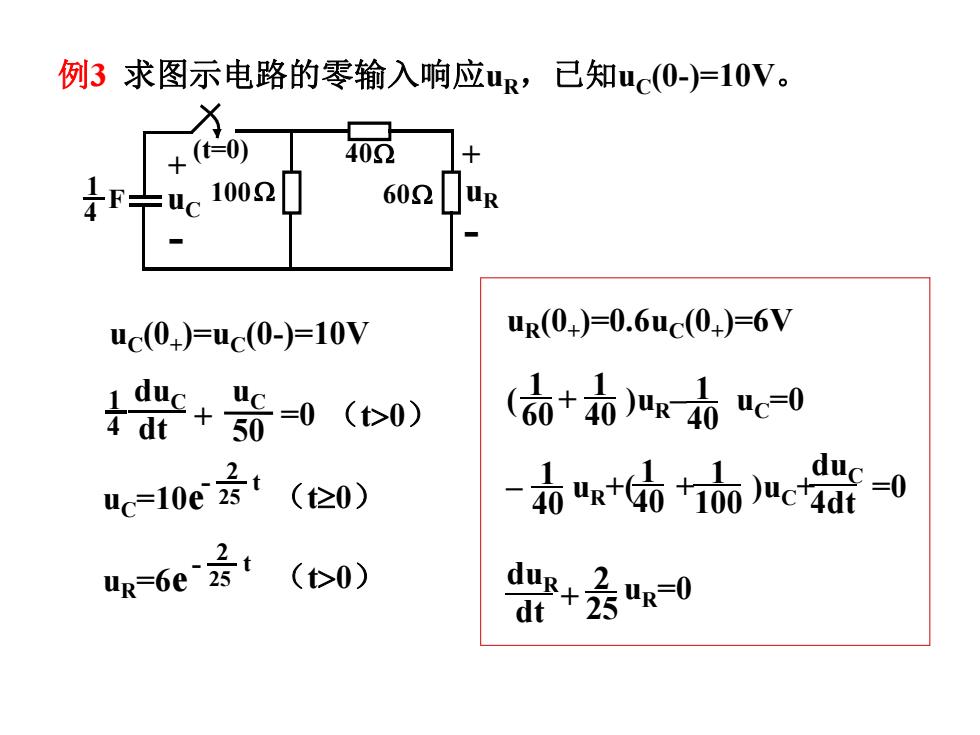
例3求图示电路的零输入响应u取,己知uc(0-)=10V。 +(0) 402 F-c1002 602uR uc(0+)=uc(0-)=10V uR(04)=0.6uc(0+)=6V 4c+6-0(0) 4 dt +50 (动+0加0"e0 uc=10e云·(伦0) duc =0 -0+h+) -6e号i (0) 0+会0
ֻ3 ≲മ⽪⭥䐟Ⲵ䴦䗃ޕ૽ᓄuRˈᐢ⸕uC(0-)=10VDŽ uR + - 1 4 F 100: 60: 40: uC + - (t=0) 1 4 =0 duC dt uC 50 + ˄t!0˅ uC=10e - 25 ˄tt0˅ 2 t uR=6e - 25 2 t ˄t!0˅ uC(0+ )=uC(0-)=10V uR(0+ )=0.6uC(0+ )=6V 60 1 1 40 1 40 ( + )uR– uC=0 1 40 1 40 – uR+( + )uC+ =0 4dt duC 100 1 dt duR 2 25 + uR=0
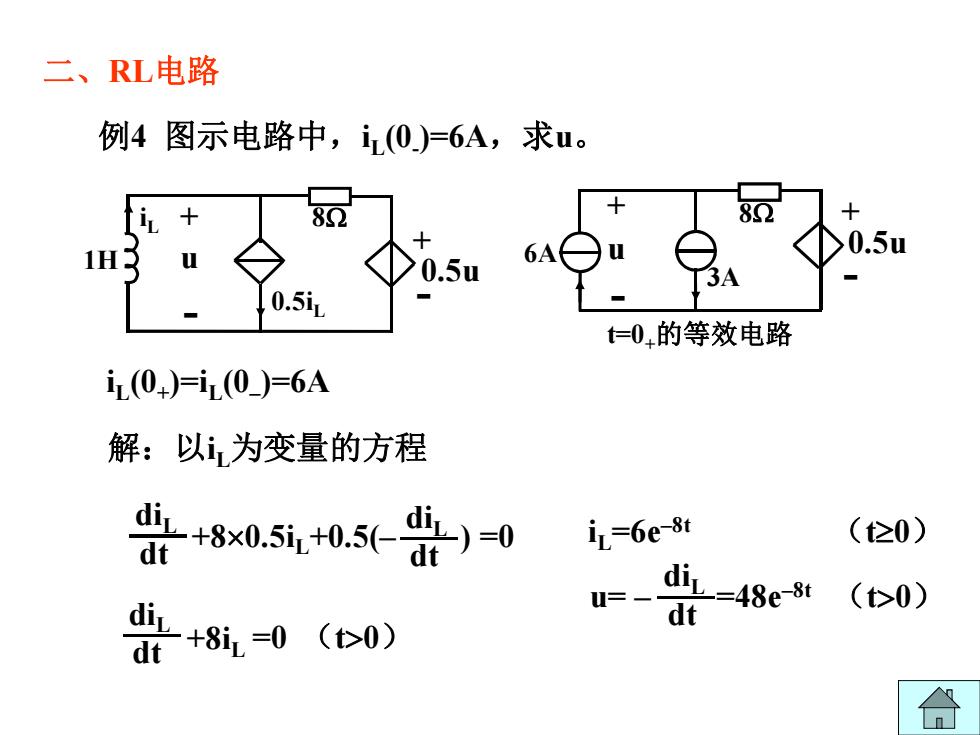
二、RL电路 例4图示电路中,i(0)=6A,求u 0.5u 0.5u 6A 0.5i1 t仁0,的等效电路 i(0)=i(0)=6A 解:以i为变量的方程 ÷+8x05u+05(盟)0 iL-6e-8t (≥0) +8i,.=0(0) 、 diL=48e-8 (t0) dt
+ - + - u 0.5iL 1H 8: 0.5u iL ֻ4 മ⽪⭥䐟ѝˈiL (0- )=6Aˈ≲uDŽ 䀓˖ԕiLѪਈ䟿Ⲵᯩ〻 =0 diL dt +8iL ˄t!0˅ iL (0+ )=iL (0– )=6A diL dt +8u0.5iL+0.5(– ) =0 diL dt diL dt u= – =48e–8t ˄t!0˅ iL=6e–8t ˄tt0˅ ҼǃRL⭥䐟 + 8: - 6A u 3A 0.5u + - t=0+Ⲵㅹ᭸⭥䐟