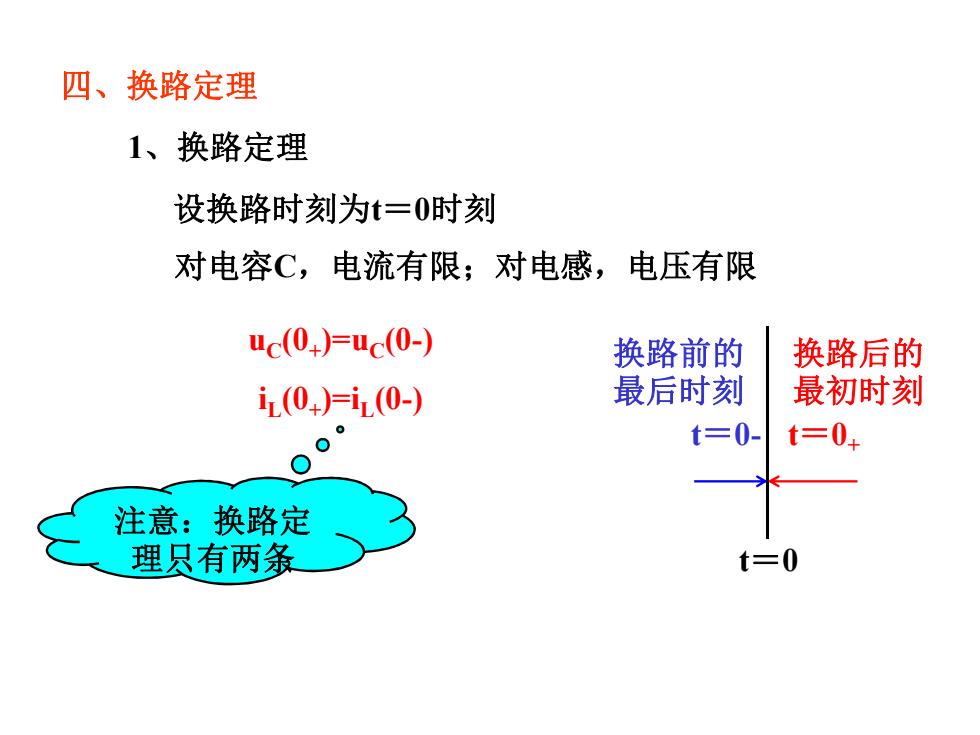
四、换路定理 1、换路定理 设换路时刻为t=0时刻 对电容C,电流有限;对电感,电压有限 uc(0)=uc(0-) 换路前的 换路后的 i(04)=i(0-) 最后时刻 最初时刻 0 t=0- t=0: 注意:换路定 理只有两条 t=0
䇮ᦒ䐟ᰦѪt˙0ᰦ ሩ⭥ᇩCˈ⭥⍱ᴹ䲀˗ሩ⭥ᝏˈ⭥ᴹ䲀 ഋǃᦒ䐟ᇊ⨶ t˙0 t˙0- t˙0+ ᦒ䐟ࡽⲴ ᴰਾᰦ ᦒ䐟ਾⲴ ᰦࡍᴰ uC(0+ )=uC(0-) iL (0+ )=iL (0-) ⌘˖ᦒ䐟ᇊ ⨶ਚᴹєᶑ 1ǃᦒ䐟ᇊ⨶

2、换路定理的应用(求解过渡过程的初始值) 分析过渡过程从=0时开始,因此,t=0时刻 为过渡过程的起点。 (1)uc0+),(0)为初始条件 (2)求解初始值的步骤: ·画出t=0-时的电路,求出uc(0-)和i(0-)。当换路 前电路处于稳态,则C视为开路,L视为短路。 ·根据换路定理求出uc(0+)和i(0+)。 ·画出0时的电路: C一电压值为uc0+)的电压源; L一电流值为(0+)的电流源。 ·按0时的电路,求出其他所需的初始值
2ǃᦒ䐟ᇊ⨶Ⲵᓄ⭘˄≲䀓䗷䗷〻Ⲵࡍ٬˅ ࠶᷀䗷䗷〻Ӿt˙0+ᰦᔰˈഐ↔ˈ t˙0+ᰦ Ѫ䗷䗷〻Ⲵ䎧⛩DŽ ˄1˅uC(0+ ) ˈiL (0+ )ѪࡍᶑԦ ˄2˅≲䀓ࡍ٬Ⲵ↕僔˖ • ⭫ࠪt˙0-ᰦⲴ⭥䐟ˈ≲ࠪuC(0-)઼iL (0-)DŽᖃᦒ䐟 ࡽ⭥䐟༴ҾっᘱˈࡉC㿶Ѫᔰ䐟ˈL㿶Ѫ⸝䐟DŽ • ṩᦞᦒ䐟ᇊ⨶≲ࠪuC(0+ )઼iL (0+ )DŽ • ⭫ࠪ0+ᰦⲴ⭥䐟˖ C——⭥٬ѪuC(0+ )Ⲵ⭥Ⓚ˗ L——⭥⍱٬ѪiL (0+ )Ⲵ⭥⍱ⓀDŽ • ᤹0+ᰦⲴ⭥䐟ˈ≲ࠪަԆᡰ䴰Ⲵࡍ٬DŽ
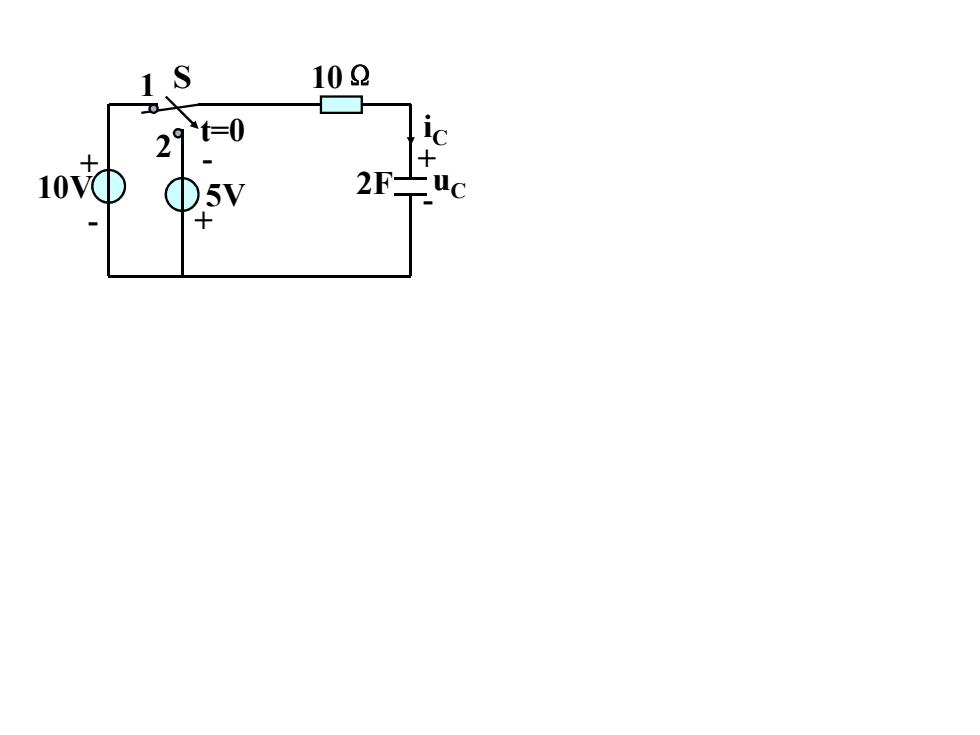
S 1 102 29 t=0 10V① )5V
S t=0 1 2 +- 10V +- 5V 2F +-u C 10 ¡ i C
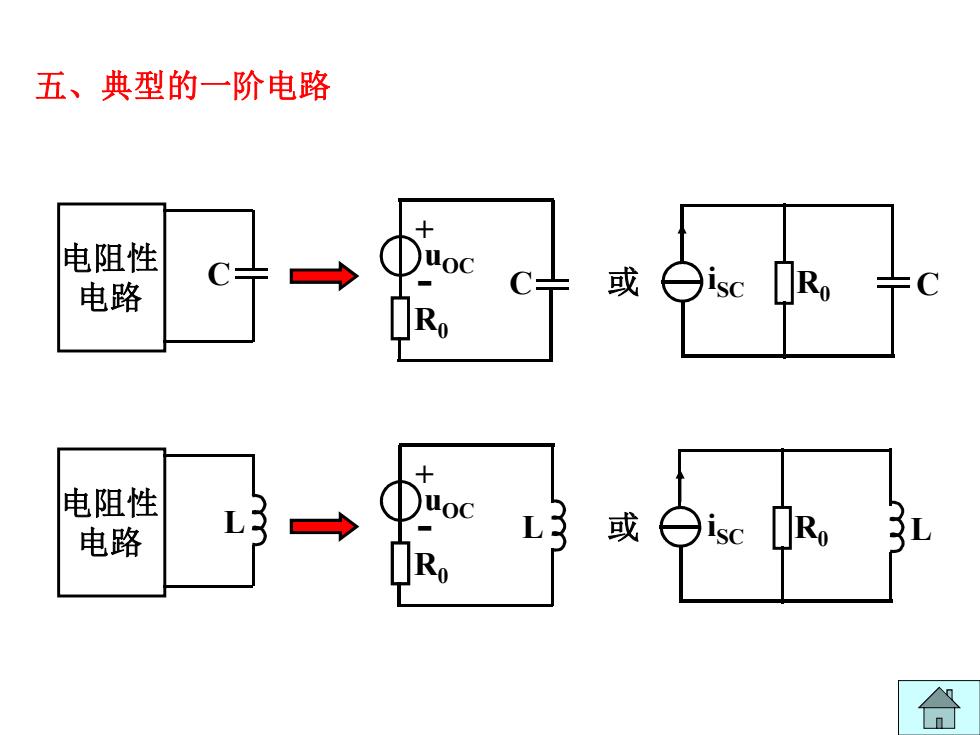
五、典型的一阶电路 电阻性 电路 或Oisc Ro 电阻性 电路 或 R n
⭥䱫ᙗ ⭥䐟 C ⭥䱫ᙗ ⭥䐟 L + - uOC R0 C + - uOC R0 L ᡆ iSC R0 C ᡆ iSC R0 L ӄǃިරⲴа䱦⭥䐟
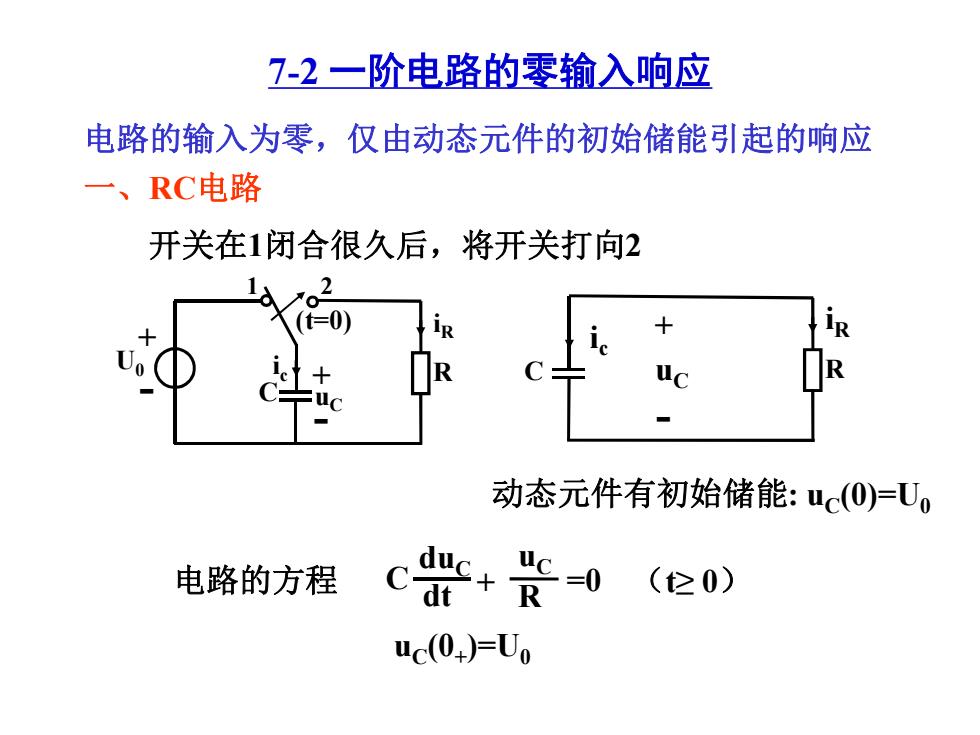
7-2一阶电路的零输入响应 电路的输入为零,仅由动态元件的初始储能引起的响应 一、RC电路 开关在1闭合很久后,将开关打向2 R R 动态元件有初始储能:uc(0)=U。 电路的方程 +1 )(0) uc(0+)=Uo
⭥䐟Ⲵ䗃ޕѪ䴦ˈӵ⭡ࣘᘱݳԦⲴࡍۘ㜭ᕅ䎧Ⲵ૽ᓄ ᔰޣ൘1䰝ਸᖸѵਾˈሶᔰޣᢃੁ2 ࣘᘱݳԦᴹࡍۘ㜭: uC(0)=U0 ⭥䐟Ⲵᯩ〻 uC(0+ )=U0 C =0 duC dt uC R + ˄W 0˅ uC i c R + iR - C аǃRC⭥䐟 uC + - i c R iR (t=0) U0 + - C 1 2 7-2 ж䱬⭫䐥Ⲻ䴬䗉ޛଃᓊ