
电阻电路的分折店结电路的图是用以表示电路几何结构的图形图中的支路和结点与电路的支路和结点一一对应G=支路,结点(1)图的定义(Graph)①图中的结点和支路各自是一个整体②移去图中的支路,与它所联接的结点依然存在,因此允许有孤立结点存在③如把结点移去,则应把与它联接的全部支路同时移去返上回页F页
⑴图的定义(Graph) G={支路,结点} 电路的图是用以表示电路几何结构的图形, 图中的支路和结点与电路的支路和结点一一对应。 ①图中的结点和支路各自是一个整体。 ②移去图中的支路,与它所联接的结点依然 存在,因此允许有孤立结点存在。 ③如把结点移去,则应把与它联 接的全部支路同时移去。 上 页 下 页 结论 返 回

购搬价从图G的一个结点出发沿着一些支(2)路径路连续移动到达另一结点所经过的支路构成路径。(3)连通图图G的任意两结点间至少有一条路径时称为连通图,非连通图至少存在两个分离部分。返上回下页
从图G的一个结点出发沿着一些支 路连续移动到达另一结点所经过的 支路构成路径。 (2)路径 (3)连通图 图G的任意两结点间至少有一条路 径时称为连通图,非连通图至少存 在两个分离部分。 返 回 上 页 下 页
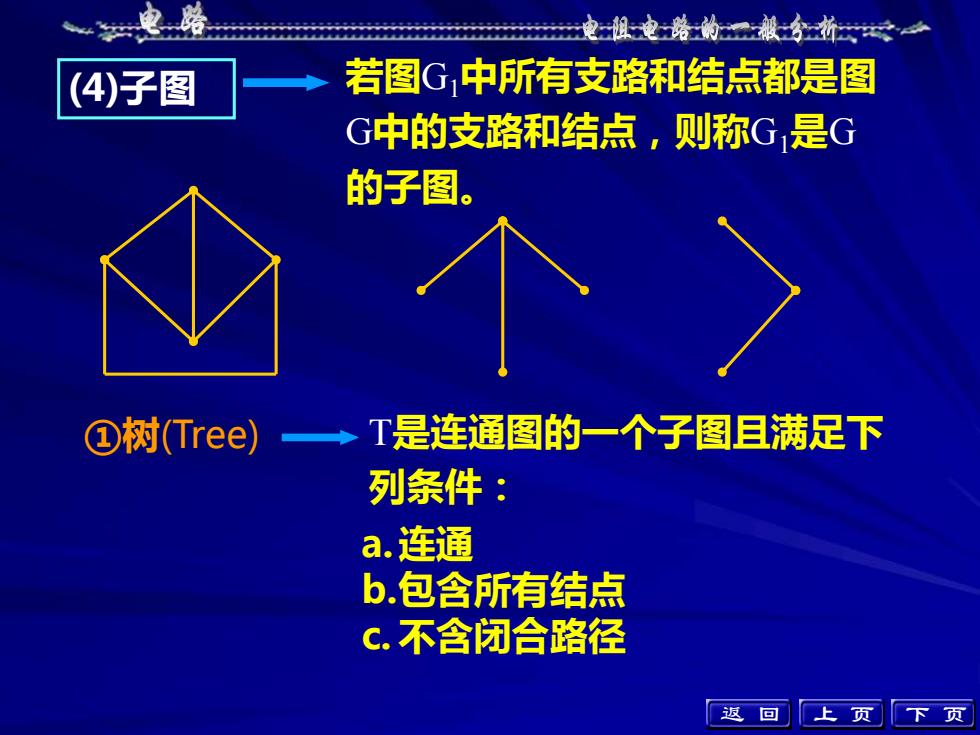
路电阻电路的般分折若图G,中所有支路和结点都是图(4)子图G中的支路和结点,则称G是G的子图。T是连通图的一个子图且满足下→①树(Tree)列条件:a.连通b.包含所有结点C.不含闭合路径返上回页N
(4)子图 若图G1中所有支路和结点都是图 G中的支路和结点,则称G1是G 的子图。 ①树(Tree) T是连通图的一个子图且满足下 列条件: a.连通 b.包含所有结点 c. 不含闭合路径 返 回 上 页 下 页
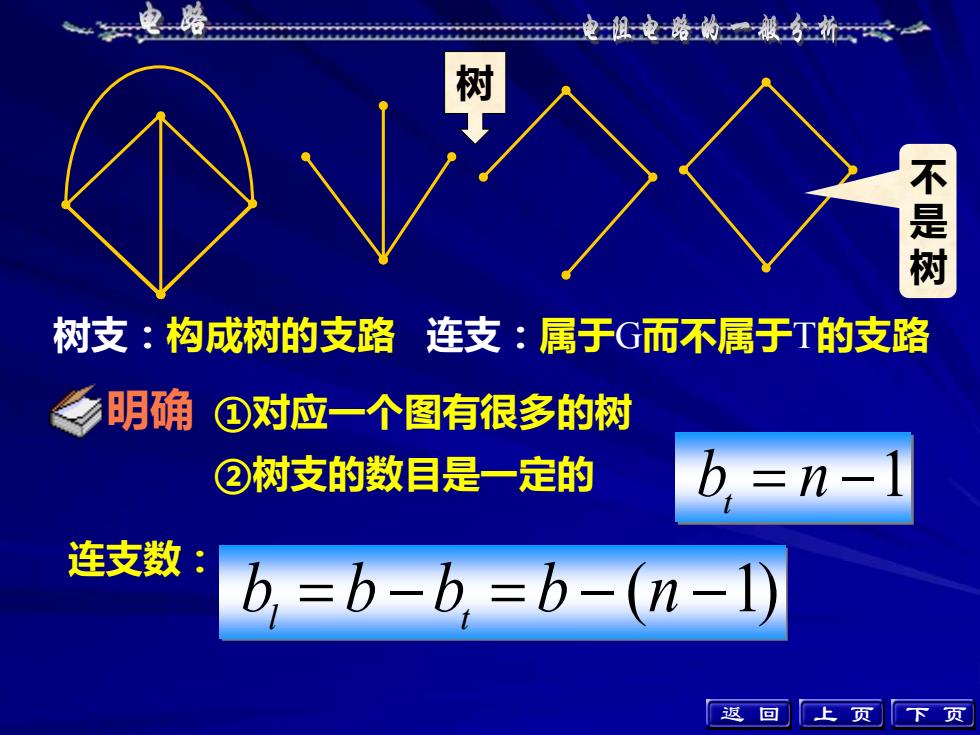
电路的搬分折山树不是树树支:构成树的支路连支:属于G而不属于T的支路明确①对应一个图有很多的树②树支的数目是一定的h,=n-l连支数b, =b-b, =b-(n-l)返上回F页
树支:构成树的支路 连支:属于G而不属于T的支路 ②树支的数目是一定的 连支数: 不 是 树 b = n −1 t b = b − b = b − (n −1) l t 树 ①对应一个图有很多的树 上 页 下 页 明确 返 回
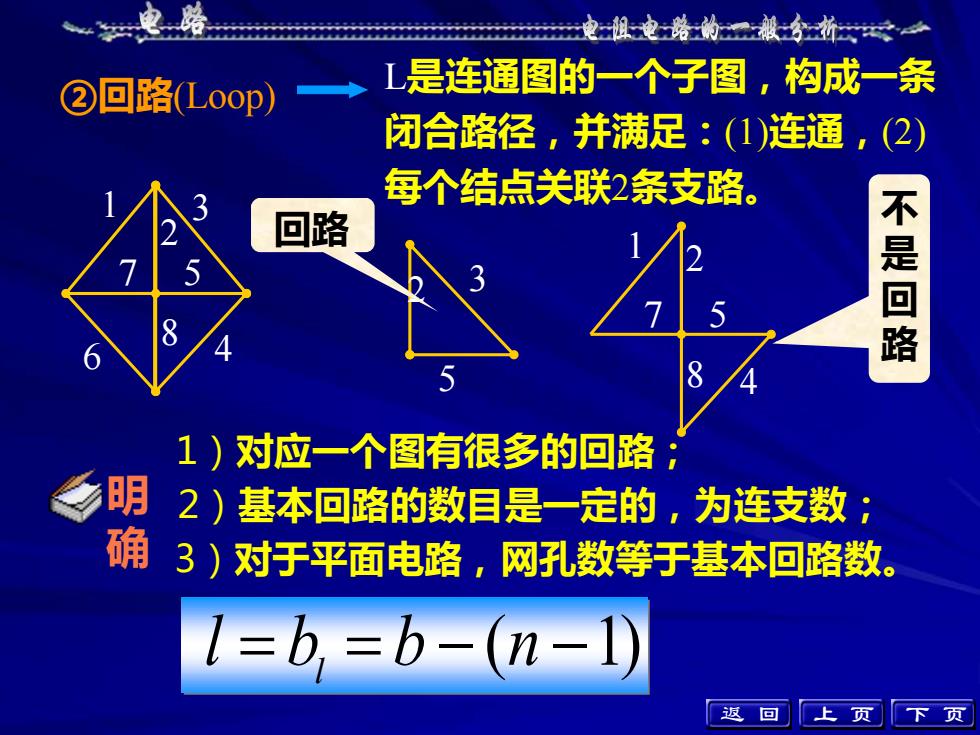
福电阻电路的般分折山是连通图的一个子图,构成一条②回路(Loop)闭合路径,并满足:(1)连通,(2)每个结点关联2条支路不是回路回路1)对应一个图有很多的回路明2)基本回路的数目是一定的,为连支数;肉确3)对于平面电路,网孔数等于基本回路数。l =b, =b-(n-l)返上回页1
②回路(Loop) L是连通图的一个子图,构成一条 闭合路径,并满足:(1)连通,(2) 1 每个结点关联2条支路。 2 3 4 5 6 7 8 2 5 3 1 2 4 7 5 8 不 是 回 路 回路 2)基本回路的数目是一定的,为连支数; l = b = b − (n −1) l 1)对应一个图有很多的回路; 3)对于平面电路,网孔数等于基本回路数。 上 页 下 页 明 确 返 回