
1.3 Vectors and Polar Forms 15 1+2 0 Figure 1.6 Vector addition. Letv and v denote the vectors determined by the points and z.respectively. The vector sum v=v+v2 is given by the parallelogram law,which is illu stra ed in Fig.1.6.If =x1+iyn and z =x2+iy2,then the terminal point in Fig.1.6 has the coor of the vector dinates (x1+x2.yI+y):that is.it corresponds to the point 21+22.Thus we see that the correspondence between complex mmbers and planar vectors carries over to the operation of addition. Hereafter,the vector determined by the pointz will be simply called the veto Recall the ometric fact that the length of any side of a triangle is less thanor equal to the sum of the lengths of the other two sides.If we apply this theorem to the triangle in Fig.1.6 with vertices 0,z1,and +z2,we deduce a very important law relating the magnitudes of complex numbers and their sum: Triangle Inequality.For any two complex numbers z and zz.we have lz1+z2l≤l3l+l2. (1) The triangle inequality can easily be extended to more than two complex numbers, The vector z,when added to the vector obviously yields the vecto Thusabpas thedirectdine sefrom(17) Applying the geometric theorem to the triangle in Fig.1.7,we deduce another form of the triangle inequality: l22l≤ll+lz2-zil 9 l22l-lzl≤l22-z1l. (2) Inequality(2)states that the difference in the lengths of any two sides of a triangle is no greater than the length of the third side. Example 1 Prove that the three distinct points2, and z3 lie on the same straight line if and only if z3-z2 =c(22-Z1)for some real number c

Complex Numbers 16 Figure 1.7 Vector subtraction Figure 1.8 Collinear points. Solution. Recall that two vectors are parallel if and only if one is a(real)scala multiple of In the nguage of complex numbers,this says thatis parallel real.From Fig1.we see that the condition that the pointsand be colinear is equivalent to the statement that the vector 3-z is parallel to the vector Using our characterization of parallelism,the conclusion follows immediately. ◆ There is another set of parameters that characterize the vector from the origin to the point z(other,that is,than the real and imaginary parts of z),which more inti- mately reflects its interpretation as an object with magnitude and direction.These are the polar coordinates,r and,of the point.The coordinater is the distance from the to,and is the angle of inclination of the measured positively in a sens fromh positive real axis(and thus negative when measured clockwise)(see Fig.1.9).We shall always measure angles in radians in this book:the use of degree measure is fine for visualization purposes,but it becomes quite treach- erous in any discipline where calculus is involved.Notice thatris the modulus,or absolute value,of z and is neve negative:r =Izl. FromFig.1.9 we readily derive the equations expressing the rectangular(or Carte- sin)coordinates(y)in terms of the polar coordinates(r,): x=rcos0; y=r sine. Q

1.3 Vectors and Polar Forms 17 Flgure 19 Polar coordinates. On the other hand,the expr ressions for(r.)in terms of(xy)contain some minor but troublesome complications.Indeed the coordinater is given,unambiguously,by r=vx2+y2=kl (4) However,observe that although it is certainly true that tan=y/x,the natural con- clusion 6=an-1() is invalid for points z in the second and third quadrants(since the standard interpre tation of the arctangent function places its range in the first and fourth quadran Since an angle is fixed by its sine ad cosine,is uniquely determined by the pair of equations cos= (5) but in practice we usually compute tan(/x)and adjust for the quadrant problem by adding or subtracting (radians)when appropriate (see Prob.14). The nuisance aspects of do not end here,however.Even usig Egs.(5)one can of 2.To accommodate this feature we shall call the value of any of these angles ar argieut,or phase.of,denoted ang z. Thus if 0o qualifies as a value of arg z,then so do ±2元,0土4r,0±6π., and every value of argmust be one of these.In particular,the values of argiare ππ 22±2,2±4… An alterative way to express arg is to write it as the ser agz={+2k#:k=0土1.2.小

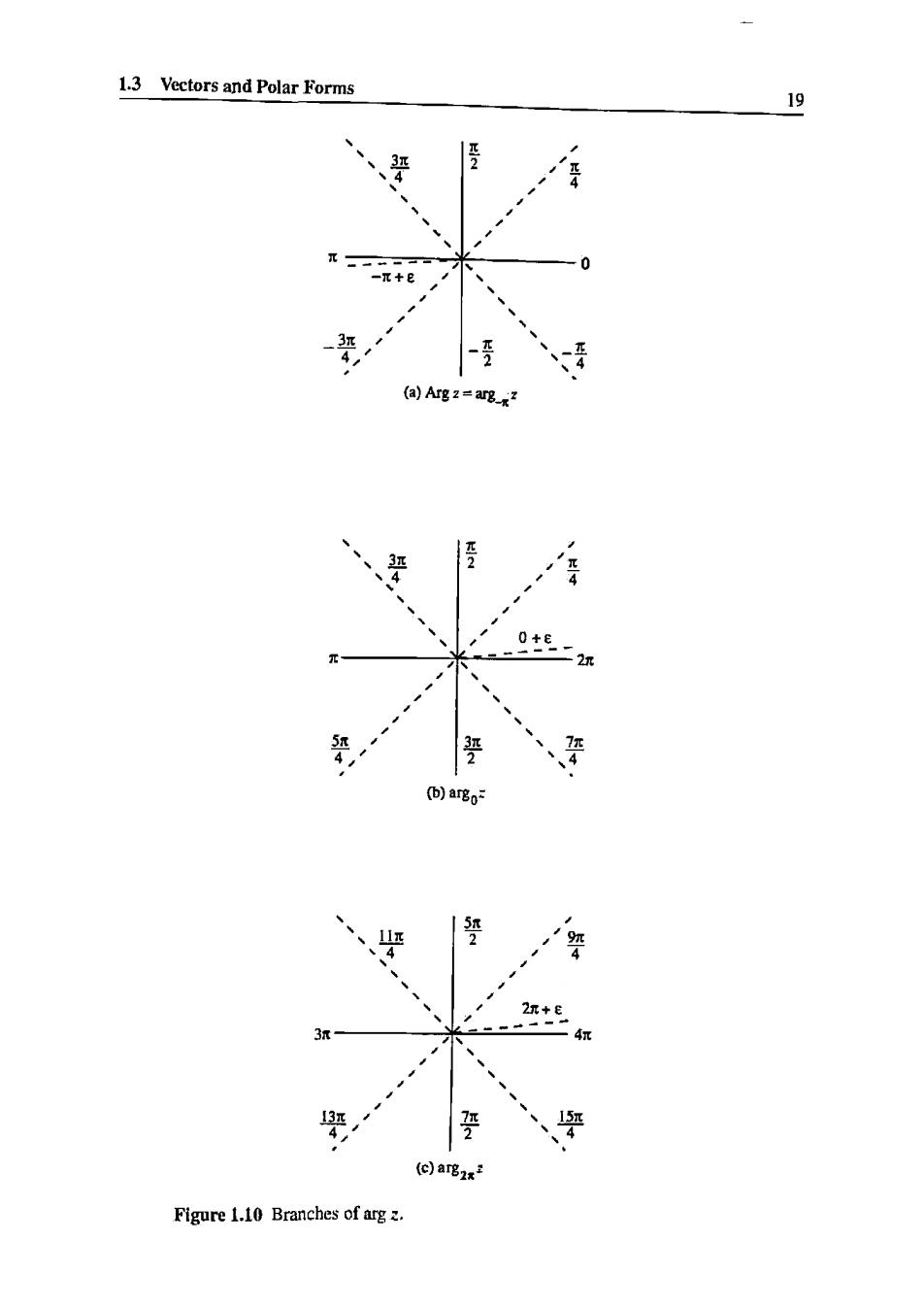
18 Conplex Numbers and we write ang/=+2k k=0.±1,士2,). It is convenient to have a notation for some definite value of argz.Notice that any halfopen interval of length2 will contain one and only one value of the argument. By specifying such an interval we say that we have selected a particularranch of arg Figure .hree possible branch(Fig1.(a) depicts the branch that selects the value of argz from the interval (,it is known the principal value of the argimnent and is denoted Arg z(with capital A).The luc is most commonly used in complex arithmetic computer codes;it is inherently discontinous,jumping by 2 as crosses the negative real axis.This line of discontinuities is known as the branch cnt. Of course,any branch of argz must have a jump of 2 somewhere.The branch pcted.b)is ntinuous on the ve real axis,taking values from interval (0.]The branch in Fig,1.10(c)has the same branch cut but selects values from the interval (2.41. The notation arg zis used for the branch of argz taking values from the interva (,+2 ]Thus arg_ is the principal value Arg,and the branches depicted in Fig.1.10(b)and 1.0(c),respectively,are argozand arg.Note that arg cannoi be sensibly lefined for any branch. With these conventions in hand.one can now write z=x+ly in the polar form [recall Eg.(3)] z=x+iy =r(cose +i sin)=rcis, (6) where we abbreviate the"cosine plus i sine"operator as cis. Example 2 Find arg(l+√3i)and write 1+√3 iin polar form. Solution. Note that r =1+3l =2 and that the equations cos 1/2, sine =3/2 are satisfied by 0 =x/3.Hence arg(1+i)=/3+2k,k= 0,1,2.… in particular,Arg(l+√3i)=π/3].The polar form of I+√3iis 2cosπ/3+isinπ/3)=2cisπ/3. In many circumstances one of the formsx+iy orrcise may be more suitable than the other.The rectangula r form,for example,is very convenient for addition or surwhereas the polarfom can bea monstrosity (see Prob.21)Onthe ther hand,the polar fo multiplica orm lends a very interesting geomeric interpretation to the process of tion.If we let then we compute z2=r2(cos0 +isin 02). z1z2=rir2 [(cos 0 cos0-sin01 sin0)+i (sin 01 cos+cos01 sin02)], and so z1z2=rnr2[cos(01+02)+isin(a:+2)1
1.3 Vectors and Polar Forms 19 、 、 (a)Argz 间)ar0 2+ ,4元 (d)ar喀2x2 Figure 1.10 Branches of arg