
Chapter 5.Approximation ann①的实部为0。an是一个纯虚数,故可令ann①=iy(Y为实数). Ψm>|v0>+∑awIv0)>=w0>+a0|w0>+∑a知Iw0> k= kn =Ψ9>+yv0>+入∑a"1y0>=(1+iy)川y0>+元∑a1y> =e1y0>+∑a1y> =e">+a1w> 上式结果表明,展开式中,a2n (①)|业。(o)>项的存在只不过是使整 个态矢量|中。>增加了一个相因字,这是无关紧要的。所以我们可取γ =0,即anna=0。这样一来, |yw9>+2∑1y°>=v0>+n ≤y1i1y≥ k E0-E wg>+2 ≤y1i田Iw> E()-E() > w>+2 ≤g11y"≥1y0> E0-E9 16
Chapter 5. Approximation 16 an n(1)的实部为0。an n(1) 是一个纯虚数,故可令an n(1)= i γ (γ 为实数). λ+>ψ>≈ψ ∑ >ψ = )0()1( 1 )0( || | kkn k n n a +>= +> ∑ > ≠ )0( )0()1( )0()1( | | | kkn nk n a nnn λψλψ a ψ λ+>ψγλ+>ψ= ∑ >ψ ≠ )0( )0( )0()1( | | | kkn nk n n i a += +> ∑ > ≠ )0( )0()1( |)1( | kkn nk i n λψγλ a ψ = +> ∑ > ≠ )0( )0()1( | | kkn nk n i e λψ a ψ γλ ⎟⎟⎠⎞ ⎜⎜⎝⎛ = +> ∑ > ≠ )0( )0()1( | | kn k nk n i e λψ a ψ γλ 上式结果表明,展开式中,an n(1) |ψn (0) > 项的存在只不过是使整 个态矢量|ψn > 增加了一个相因子,这是无关紧要的。所以我们可取 γ = 0,即 an n(1) = 0。这样一来, +>>= ∑ > ∞ ≠ )0( )0()1( || | kkn nk n n a ψλψψ > − < > +>= ∑ ∞ ≠ )0( )0()0( )0()1()0( )0( | | ˆ | | k n k k n nk n EE H ψ ψ ψ λψ > − < ′ > +>= ∑ ∞ ≠ )0( )0()0( )0( )0( )0( | | ˆ | | k kn k n nk n EE H ψ ψψ ψ > − < > +>= ∑ ∞ ≠ )0( )0()0( )0()1()0( )0( | | ˆ | | k n k k n nk n EE H ψ ψλψ ψ

Chapter 5. Approximation +2 H如 a n E- 即IΨn>Ψ0>+y9> (三)能量的二阶修正 与求态矢的一阶修正一样,将1业.②>按|中0>展开: y×21w×g1w21g"> 与引四>展开式一起代入关于2的第三式 io-E"宫g1w”>-i-E"店g1y”>+E9y”> 言E"-E2v">-i-Egg1y,”>+E1g> 17
Chapter 5. Approximation 17 (0) (0) (0) (0) | | kn n k k n n k H E E ψ ψ ∞ ≠ ′ = >+ > − ∑ 与求态矢的一阶修正一样,将|ψn (2) > 按 |ψn (0) > 展开: >= ∑ >< >= ∑ > ∞ = ∞ = )0()2( 1 )0( )2()0( 1 )2( | | | | kkn k k nk k n ψ ψψψ a ψ 与|ψn (1) >展开式一起代入 关于 λ2 的第三式 − ∑ −−>= ∑ +> > ∞ = ∞ = )0()1( )0()2( 1 )0()2( )1()1( 1 )0()0( |] | ˆ |] [ ˆ [ kkn nn k kkn n k n aEH ψ aEH ψ E ψ ∑ − −−>= ∑ +> > ∞ = ∞ = )0()1( )0()2( 1 )0()2()0()0( )1()1( 1 |] | ˆ [ |] [ kn k n n k k knn k n k aEE ψ EH a ψ E ψ >ψ+>ψ>=ψ )0( )1( ||| 即 n n n (三)能量的二阶修正 (1) (0) (0) kn kn n k H a E E ′ = −
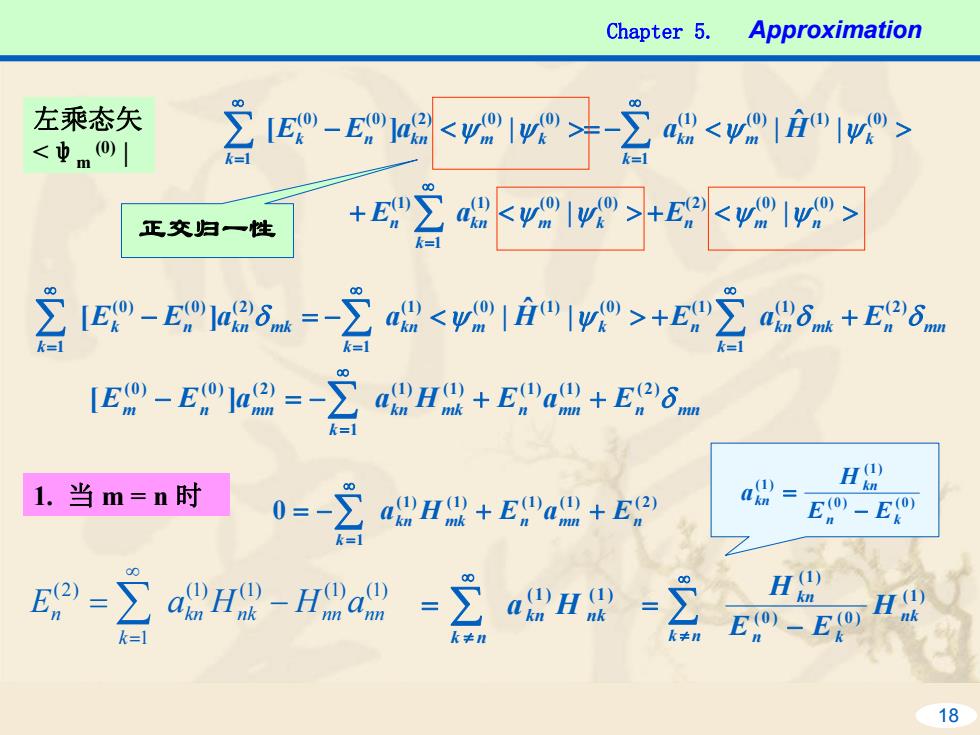
Chapter 5. Approximation 左乘态矢 <中m0| 空g-w宫2<i> 正交归一性 +E>+1g> 言"-公5=-宫8<川>+25+E6- k=雪 Eg-Ega2=2H盟+Ea+E6 1.当m=n时 a= HO E-E =∑日 H nk k= 18
Chapter 5. Approximation 18 mnnmkkn k kn m k n k mkknnk k aEE δ a ψ H ψ EaE δδ)1( )2( 1 )1()0()1()0()1( 1 )2()0()0( 1 | ˆ ∑ − ][ ∑ <−= | +> ∑ + ∞ = ∞ = ∞ = 左乘态矢 <ψm (0) | 1. 当 m = n 时 )2()1()1()1()1( 1 0 mkkn mnn n k −= ∑ ++ EaEHa ∞ = )1()1()1()1( 1 )2( nkkn nnnn k n =∑ − aHHaE ∞ = )1()1( nkkn nk ∑ Ha ∞ ≠ = )1( )0()0( )1( nk n k kn nk H EE H − = ∑ ∞ ≠ mkkn mnn mnn k m aEE mnn EaEHa δ)2()1()1()1()1( 1 )2()0()0( [ − ] −= ∑ ++ ∞ = + < <+> > <− <−>= > ∑ ∑ ∑ ∞ = ∞ = ∞ = )0()0()2()0()0()1( 1 )1( )0()1()0()1( 1 )0()0()2()0()0( 1 | | | ˆ |][ | kmkn n nm k n mkn k k kmknnk k aE E aEE a H ψψ ψψ ψψ ψψ 正交归一性 )0()0( )1( )1( n k kn kn EE H a − =

Chapter 5.Approximation 在推导中使用了 E-EO k≠n E-E) 微扰矩阵的厄密性, H=<1i四1y0>=<v.1Aa+Iy> =<y01iIyw">=H四 Ea1= H82 k≠n E)-Eo) 2.当m≠n时 能量二级修正: PE- g E-EO 乏KTI”o=E EO-EO (同m=n情形) n 19
Chapter 5. Approximation 19 )0()0( *)1()1( n k knkn nk EE HH − = ∑ ∞ ≠ )0()0( 2)1( || n k kn nk EE H − = ∑ ∞ ≠ 在推导中使用了 微扰矩阵的厄密性. *)1( *)0()1()0( | ˆ Hkn =<ψ k | H ψ n > =< > + )0()1()0( | ˆ | ψ n H ψ k =< >)0()1()0( | ˆ | ψ n H ψ k )1( = Hnk )0()0( 2)1( )2( || n k kn nk n EE H E − ∴ = ∑ ∞ ≠ 能量二级修正: )0()0( 2)1( 2)2(2 || n k kn nk n EE H E − = ∑ ∞ ≠ λλ )0()0( 2)0()1()0( || ˆ || kn k n nk EE H − < > =∑ ∞ ≠ ψλψ )0()0( )0( 2)0( || ˆ || kn k n nk EE H − < ′ > =∑ ∞ ≠ ψψ 2 (2) (0) (0) | | kn n k n n k H E E E ∞ ≠ ′ = = − ∑ (同m=n情形) 2. 当 m ≠ n 时

Chapter 5. Approximation 在计及二阶修正后,扰动体系能量本征值由下式给出: E,=E++E2=E+H+2H E0)-E0 态矢量: 0 ∑aw> k= [E-E=-∑aH+E"a n k=1 ae) aH mn mk H E0)-E0) m HH HH E-EHEO-E EO-EP 通常态矢量只求解到一阶微扰即可。 20
Chapter 5. Approximation 20 (0) (0) (2) (1) (1) (1) (1) 1 [ ] m n mn kn mk n mn k E E a aH Ea ∞ = − =− + ∑ (1) (1) (1) (1) (2) (0) (0) (0) (0) 1 kn mk nn mn mn k nmnm aH H a a EE EE ∞ = = − − − ∑ 在计及二阶修正后,扰动体系能量本征值由下式给出: 2 (0) (1) 2 (2) (0) (0) (0) | | kn n n n n n nn k n n k H EE E E E H E E λ λ ∞ ≠ ′ =+ + =++ ′ − ∑ 2)0()0( )1()1( )0()0()0()0( )1()1( [ ][ ][] n m mnnn n knm mkkn nk EE HH EEEE HH − − − − = ∑ ∞ ≠ 态矢量: (2) (2) (0) 1 | | n kn k k ψ ψ a ∞ = >= ∑ > 通常态矢量只求解到一阶微扰即可