
例 相控阵 a 波束指向: B.=arc cos(- kd 当α=0时,B=90°,即阵因子方向图最大指向与阵轴垂直,为侧射阵。 当a=±kd时,Bn=0,180°,即最大指向在阵轴方向,称为端射阵。 当α为其它值时,称为扫描阵。 馈电相位: a=-kd cos B Nkd (cosB-cos B.)】 S()=I。 方向图函数: kd sin2(cosB-cosB.】
波束指向: 馈电相位: 方向图函数:

对于均匀激励: F(0)= N sind,( 8=10 06=15 0 阵列扫描时波瓣会展宽.对于一 0 50 大型的阵列,波束展宽~sec0o: As the array is scanned,the linear array fan beam pattern takes on the conical shape.For the o dependence
对于均匀激励: 0 0 0 0 ( ) ( ) sin ( ) sin x x N d u u d u u F N 阵列扫描时波瓣会展宽.对于一 大型的阵列,波束展宽 ~sec0. As the array is scanned, the linear array fan beam pattern takes on the conical shape. For the dependence

波束宽度 ·对于均匀激励的一维线阵,侧向的3-dB波束宽度(弧度): 03=0.886/L,L=Nd ·对于非均匀激励的一维线阵,侧向的3-dB波束宽度有所展宽: 03=0.886B2/L B。:波束展宽因子;主瓣展宽的同时$LL会下降 o 对于非均匀激励的一维线阵,且波束指向扫描至,时,3-dB 波束宽度: 8=[sin'(4+0.433B,/L)-sin'(4-0.433B,元/L)]
波束宽度 • 对于均匀激励的一维线阵,侧向的3-dB波束宽度(弧度) : 3 0 0.886 / , L L Ndx • 对于非均匀激励的一维线阵,侧向的3-dB波束宽度有所展宽 : 3 0 0.886 / B L b Bb: 波束展宽因子;主瓣展宽的同时SLL会下降 • 对于非均匀激励的一维线阵,且波束指向扫描至0时, 3-dB 波束宽度: 1 1 3 0 0 sin ( 0.433 / ) sin ( 0.433 / ) b b u B L u B L
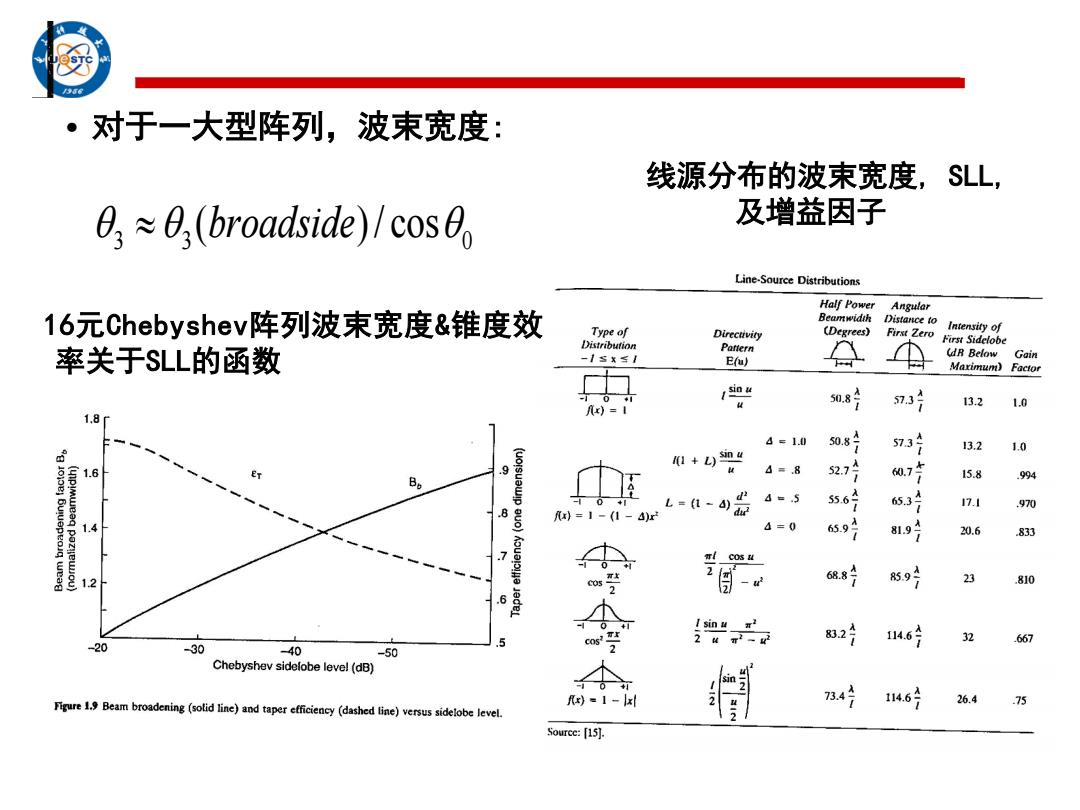
对于一大型阵列,波束宽度: 线源分布的波束宽度,SLL, 8≈6,(broadside)/cos0 及增益因子 Line-Source Distributions Half Power Angular 16元Chebyshev阵列波束宽度&锥度效 Beamwidth Distance to Type of Directivity (Degrees) First Zero Intensity of Distribution First Sidelobe 率关于SLL的函数 Pattern -1s名≤1 (dR Below E(u) Gain Marimum)Factor 0 10a 5知8片 53 13.2 1.0 fx)=I 1.8 4=1.0 08分 73片 13.2 1.0 1+)n 1.6 A=8 52.7 15.8 994 d=.5 561 6,3片 17.1 970 8 fx)=1-(1 L=t-4)证 4=0 659号 819片 20.6 833 2 1.2 688 59月 23 810 2 .6 I sin u x 832 4.6 2 .667 -20 -30 -40 -50 Chebyshev sidelobe level(dB) Figure 1.9 Beam broadening(solid line)and taper efficiency(dashed line)versus sidelobe level. )=1-x 734 146 26.4 75 Source:[15]
• 对于一大型阵列,波束宽度: 3 3 0 ( ) / cos broadside 线源分布的波束宽度, SLL, 及增益因子 16元Chebyshev阵列波束宽度&锥度效 率关于SLL的函数

阵列增益及扫描损失 ·阵列增益与方向性系数的关系为: G=(1-|r)D T:阵列输入端反射系数;受内部互耦的影响 。扫描损失: 8z=(c0s0)",n=1,3/2,2. 通常,对于缝隙阵列及偶极子阵列,在一个平面内扫描时, n=1 ·扫描盲点:对于特定的方向,所有的辐射几乎完全抵消
阵列增益及扫描损失 • 阵列增益与方向性系数的关系为: 2 0 (1 ) G D L : 阵列输入端反射系数; 受内部互耦的影响 • 扫描损失: (cos ) , n=1,3/2,2... L n 通常, 对于缝隙阵列及偶极子阵列,在一个平面内扫描时, n=1 • 扫描盲点: 对于特定的方向,所有的辐射几乎完全抵消