
其中 u=Sinθcosp,v=sinθsinp 远场条件: 2L2 10L2 R= or R= (当测量超低副瓣或零深时) λ 对于一任意阵列,通过线性叠加得到的辐射场为: Er)-eR∑f6eer 其中a:主要关联各单元的激励幅度 如果所有单元的方向图是一致的,则: E=.∑ae -jkR 可定义阵因子:F(0,p)=∑a,e:
2 2L R 远场条件: 2 10L R or (当测量超低副瓣或零深时) 对于一任意阵列,通过线性叠加得到的辐射场为: ˆ ( ) ( , ) i jkR jk i i i e a e R r r E r f 如果所有单元的方向图是一致的,则: ˆ ( , ) i jkR jk i i e a e R r r E f 其中ai主要关联各单元的激励幅度 可定义阵因子: ˆ ( , ) i jk i i F a e r r 其中 u v sin cos , sin sin

通过应用以下形式的复权重a:可实现波束的扫描: a,=|la吲e,=4,+y,+元cos0 根据求和后的函数最值,这会将波束指向扫描至(旧。,φ)方向. 所需要的激励具有与频率呈线性的相位关系,这相当于插入了 时延.因此,方向图峰值对所有的频率都是稳定的. 更一般的,扫描信号是由移项器来控制的,这样最大指向就依 赖于频率。 a;a,e-lhr" 2元 k 即只能在特定的频率下满足
通过应用以下形式的复权重ai可实现波束的扫描: 0 ˆ i jk i i a a e r r 0 0 0 0 r x y z ˆ ˆ u v ˆ ˆ cos 根据求和后的函数最值,这会将波束指向扫描至(0,0)方向. 所需要的激励具有与频率呈线性的相位关系, 这相当于插入了 时延.因此,方向图峰值对所有的频率都是稳定的. 0 0ˆ i jk i i a a e r r 更一般的,扫描信号是由移项器来控制的,这样最大指向就依 赖于频率. 0 0 2 k 即只能在特定的频率下满足
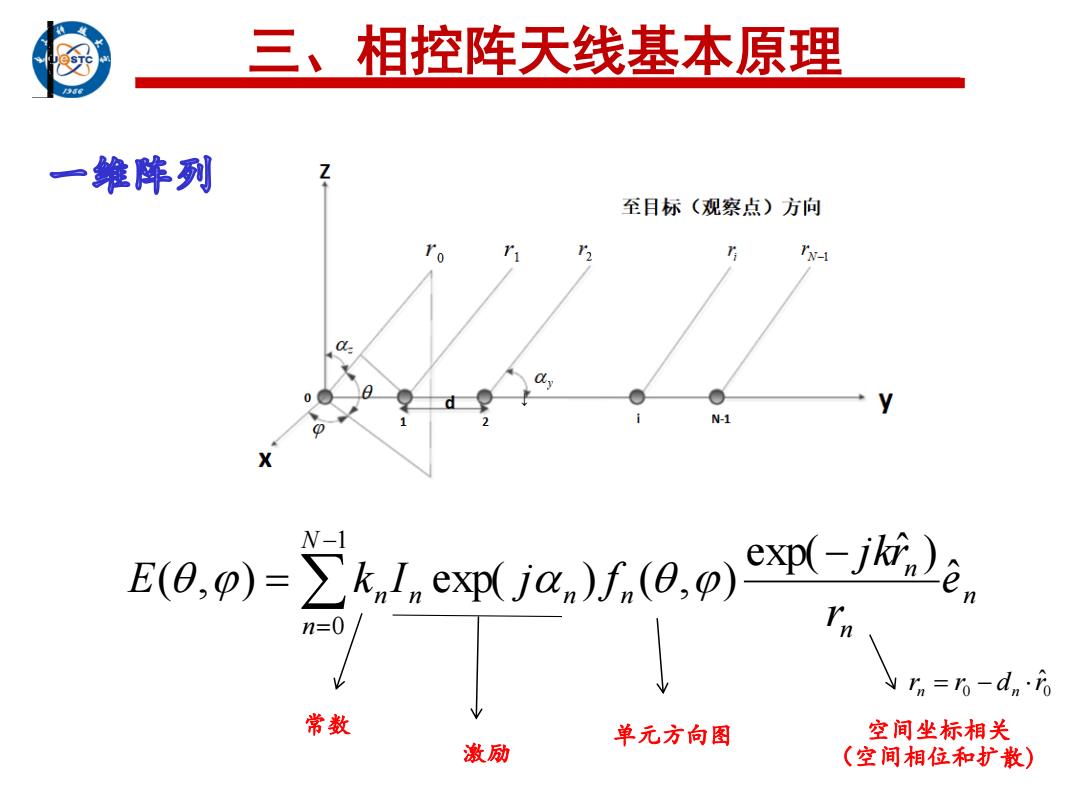
三、相控阵天线基本原理 一维阵列 至目标(观察点)方向 N-1 E(0)=>klcxpja).(0.)xj,)e W-1 n=0 n=%-dn·8 常数 单元方向图 空间坐标相关 激励 (空间相位和扩散)
三、相控阵天线基本原理 n n n N n n n n n e r j kr E k I j f ˆ exp( ˆ ) ( , ) exp( ) ( , ) 1 0 ↓ 常数 激励 单元方向图 空间坐标相关 (空间相位和扩散) 0 0 r r d r ˆ n n

In=to-dn V- E(0,p=∑k1 explj(kd元+alf.(6,pe n=0 K-长ep-k6) 广n≈远场 E(0,p)=En(0,p)f(0,0) W-1 E,(0,p)=∑1 expLj(kd+a】 n=0 dn·ò=nd sin0 N- E,(0,p)=∑1 exp[(kndsin0+a,月 n=0
n N n n n n n n E( , ) k I exp[ j(k d rˆ )] f ( , )eˆ 1 0 0 0 0 r r d r ˆ n n 1 0 0 ( , ) exp[ ( ˆ )] ( , ) ( , ) ( , ) N n n n n n n E I j k d r E E f 0 0 exp( ) r r jkr r k k n n n n 远场 1 0 ( , ) exp[ ( sin )] N n n n n E I j knd dn r ˆ 0 nd sin

sin[号(kd cosB+al 注意:其他表达 S(B)=1。 =10 sin-(kd cos B+a)】 sin() 最大波束指向: 前面已提到,均匀直线阵阵因子的最大值为: Sax=limS(w)=IoN →0 最大值出现在:1=2mπ,m=0,±1,±2, m=0时对应为主瓣,即u=kd cos B+a=0,此时,最大指向为 B.=arc cos(- kd 2 B+0=
注意:其他表达 2